13.2. Функциональные ряды

Область сходимости функционального ряда 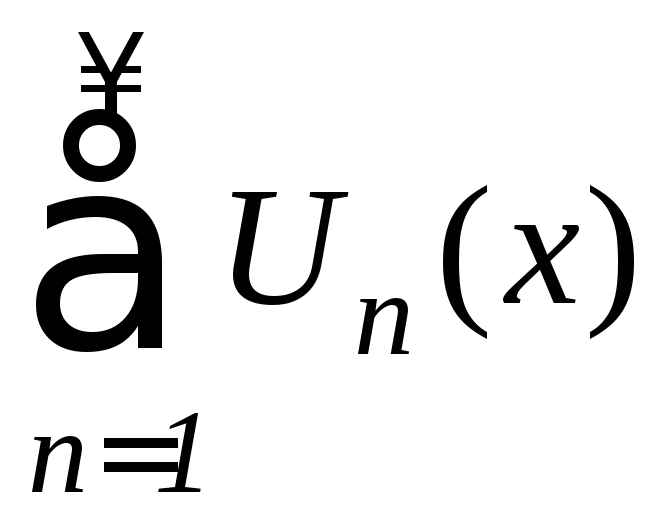, гдеU_n(x), n=1,2,3… - функции одной переменой, есть совокупность значений переменной x, при которых ряд сходится. Сумма ряда в области сходимости является некоторой функцией от x : , дляx из области сходимости.

Область сходимости определяется решением неравенства на основе достаточных признаков Даламбера или радикального признака :

.

Принадлежность концов интервала к области сходимости определяется на основе исследования числовых рядов, получающихся после подстановки значений этих концов в функциональный ряд.

В частном случае, если функциональный ряд представляет собой

степенной ряд вида , область сходимости по приведенным формулам определяется:

Здесь , гдеR – радиус сходимости .

Если функция f(x) в точке а непрерывна вместе со своими производными, то в окрестности точки x=a справедлива формула (ряд) Тейлора:

При a=0 ряд Тейлора преобразуется в ряд Маклорена :

Таблица рядов Маклорена для некоторых функций.

;

;

;

;

;

;

;

.

В скобках указаны интервалы сходимости рядов.

Разложение функций в ряд Тейлора позволяет с любой степенью точности приближенно вычислить значение функции в точке, пределы, определенный интеграл, найти частное решение дифференциального уравнения (задачу Коши) и другие.

Пример 7. Найти область сходимости ряда .

Решение. ;

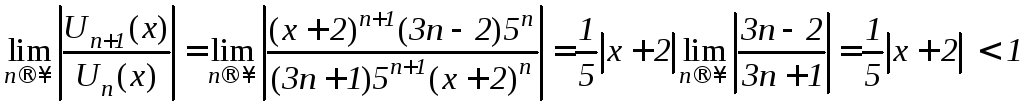< 5; -7 < х < 3.

Исследуем ряд на концах интервала (подставляем значения концов в функциональный ряд):

.

Этот знакочередующийся ряд сходится , т.к. , и члены ряда, взятые по абсолютной величине , убывают, поэтому значениевходит в область сходимости ряда.

.

Данный ряд с положительными членами расходится по признаку сравнения:

где общий член расходящегося гармонического ряда . Значит, точкане входит в область сходимости ряда.

Ответ: .

Пример 8. Найти область сходимости ряда .

Решение. ;

; .

Исследуем ряд на концах интервала.

При подстановке в функциональный ряд обеих концов интервала образуется один и тот же числовой ряд .

Этот ряд расходится по признаку сравнения его с расходящимся рядом Дирихле :

.

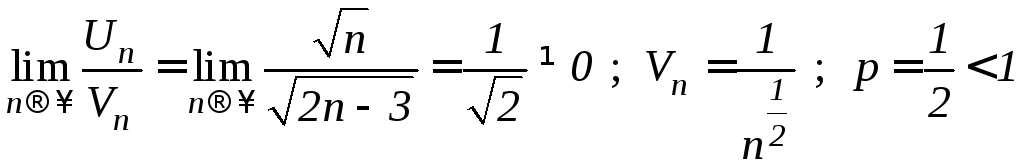Значит область сходимости функционального ряда: .

Пример 9. Найти область сходимости ряда .

Решение.

x < -2 ; .

При подстановке в функциональный ряд обеих концов интервала образуется один и тот же числовой ряд , который расходится согласно необходимому признаку сходимости:. Таким образом, область сходимости ряда:.

Пример 10. Вычислить интеграл с точностью доε = 0,001 .

Пример11. Разложить функцию в ряд Тейлора по степенямx.

Решение. Определим коэффициенты ряда Тейлора по степеням x для функции:

.

, ,

, ,

, ,

, ,

… … … … … … … … … … … … … … … …

, .

Тогда:

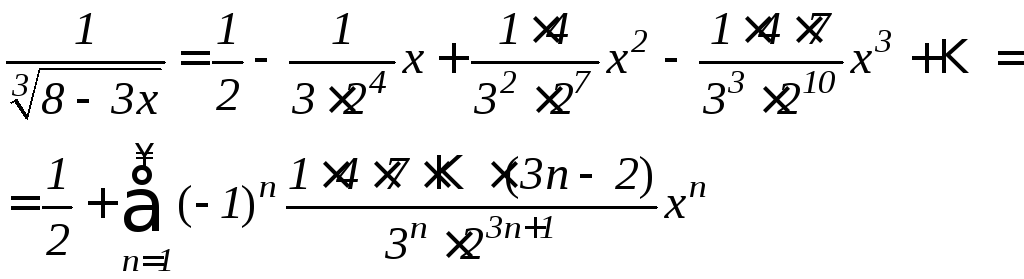
Пример 12. С помощью рядов решить дифференциальное уравнение:

; ;.

Решение. Решение дифференциального уравнения находится в виде ряда Тейлора:

,

где точка x=a определяется из начальных условий (в приведенном примере x=0 ).

Значения функции и ее производных для ряда Тейлора находятся из начальных условий непосредственно для первых членов и для остальных членов ряда путем последовательного дифференцирования исходного дифференциального уравнения, разрешенного относительно старшей производной и вычисленной в точке x=a. Для тех значений x, для которых получившийся ряд сходится, он представляет решение дифференциального уравнения.

В нашем примере:

,

,

, ,

, ,

, ,

, ,

, ,

, .

Видна закономерность:

;

; .

Подставим все значения в ряд :

Выполним преобразования:

.

.

Определим радиус сходимости этого ряда:

;

Значит полученное решение справедливо для всех x.