Введение
Контуры деталей в любой отрасли промышленности, в том числе и железнодорожных деталей, редко имеют простую форму. Гораздо чаще приходится встречаться с деталями, поверхность которых имеет сложное геометрическое строение. Для вычерчивания контура таких деталей применяются такие геометрические построения, как сопряжения, деление окружности на равные части, построение лекальных и коробовых кривых.
Представить форму и размеры детали на чертеже, можно одним из трех методов проецирования. В машиностроении наибольшее распространение получили аксонометрические и параллельные прямоугольные (ортогональные) проекции.
Выполнение графических работ и упражнений по темам разделам «Геометрические построения» и «Проекционное черчение» позволяет сформировать и закрепить умения выполнять чертежи деталей, имеющих как простую форму, так и сложную конструкцию.
Выполнение практических работ по темам «Геометрические построения» и «Проекционное черчение» позволяет сформировать у студентов следующие общие и профессиональные компетенции:
ОК 2: Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество;
ОК4: Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития;
ПК 2.2: Планировать и организовывать мероприятия по соблюдению норм безопасности условий труда;
ПК 2.3: Контролировать и оценивать качество выполняемых работ;
ПК 3.1: Оформлять техническую и технологическую документацию.
1. Краткие теоретические сведения
1.1. Геометрические построения
Деление окружности на равные части
Некоторые детали имеют элементы, равномерно распределенные по окружности. При выполнении чертежей деталей, имеющих подобные элементы, необходимо уметь делить окружность на равные части. Приемы деления окружности на равные части приведены на рис. 1
Рис. 1. Деление окружности на равные части
С достаточной точностью можно делить окружность, на любое число равных частей пользуясь таблицей коэффициентов для подсчета длины ходы.
По количеству равных отрезков на окружности (таблица 1) находим соответствующий коэффициент. При перемножении полученного коэффициента на диаметр окружности, получаем длину хорды, которую циркулем откладываем на окружности.
Таблица 1 - Коэффициент для определения длинны хорды
|
Количество частей окружности |
Коэффициент |
|
3 4 5 6 8 9 10 11 12 13 14 15 16 17 18 19 |
0,866025 0,707107 0,587785 0,433884 0,382633 0,342620 0,309017 0,281733 0,258810 0,239316 0,222521 0,207912 0,105090 0,183750 0,173648 0,164595 |
Выполнение сопряжения между двумя линиями
При вычерчивании контуров технических деталей и в других технических построениях часто приходится выполнять сопряжения (плавные переходы) от одних линий к другим. Сопряжение двух сторон угла дугой заданного радиусу дуги R выполняют в следующей последовательности:
- параллельно сторонам угла на расстоянии, равном R, проводят две вспомогательные прямые линии;
- точка пересечения этих прямых будет центром сопряжения;
- из центра сопряжения выполняют перпендикуляры на заданные прямые;
- точки пересечения перпендикуляров с заданными прямыми называют точками сопряжения;
- из центра сопряжения строят дугу радиусом R, соединяя точки сопряжения.
На рис. 2 приведены примеры построения сопряжений, когда задан радиус дуги сопряжения. В этом случае необходимо определить центр сопряжения и точки сопряжения. Обводку контура детали производят с помощью циркуля.
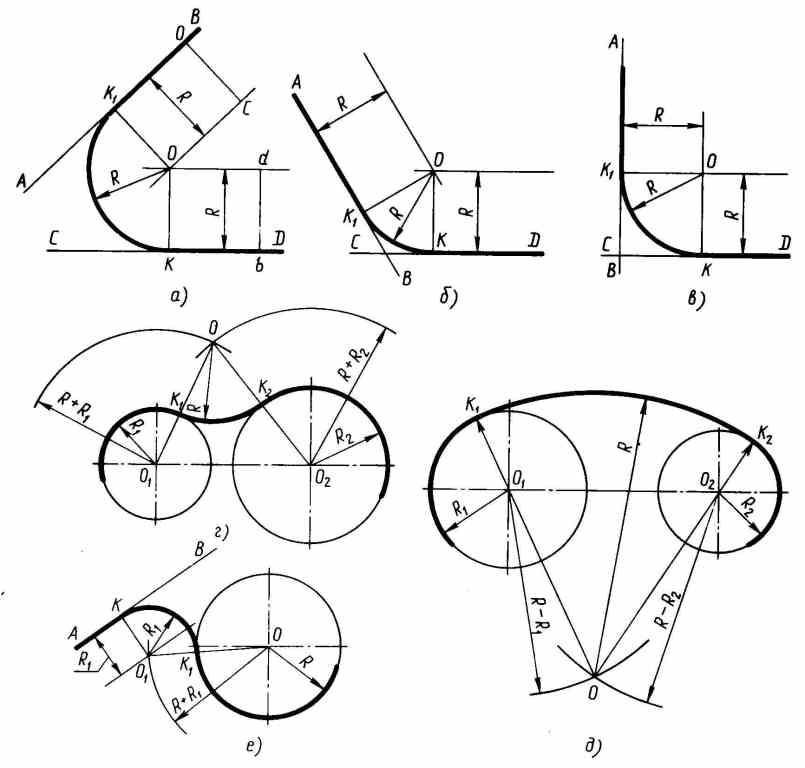
Рис. 2. Приемы построения сопряжений
В технике часто приходится вычерчивать кривые линии, составленные из большого количества малых дуг окружностей с постепенным изменением радиуса их кривизны. Такие линии невозможно провести циркулем. Эти кривые вычерчивают с помощью лекал и называют лекальными. Необходимо изучить закономерность образования лекальной кривой и нанести на чертёж ряд принадлежащих ей точек. Точки соединяют плавной кривой тонкой линией от руки, а обводку выполняют с помощью лекала.
Для обводки лекальных кривых нужно иметь набор нескольких лекал. Выбрав подходящее лекало, подгоняют кромку части лекала к возможно большему количеству найденных точек. Чтобы обвести следующий участок, нужно подогнать кромку лекала ещё к двум-трём точкам, при этом лекало должно касаться части уже обведённой кривой. Способ проведения кривой по лекалу приведён на рис. 3.
Рис. 3. Построение кривой по лекалу.
На рис. 4 показан пример построения эллипса по заданным осям AB и CD.
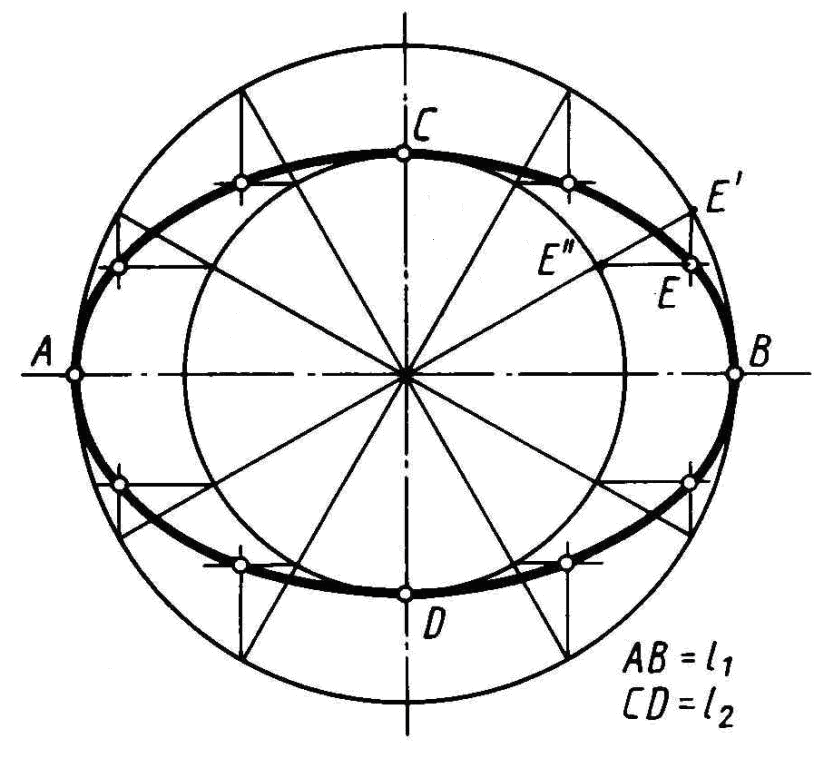
Рис. 4. Построение эллипса
На рис. 5 показан пример построения параболы с помощью деления сторон угла AOC на одинаковое количество равных частей. На рис. 6 дан пример построения эвольвенты окружности. Заданная окружность разделена на 12 равных частей. Через точки деления проведены касательные к окружности. На касательной, проведённой через точку 12, отложена длина данной окружности и разделена на 12 равных частей. Начиная от точки l на касательных к окружности, последовательно откладывают отрезки, равные 1/12 длины окружности, 1/6, 1/4 и т. д.
Рис. 5. Построение параболы
Рис. 6. Построение эвольвенты
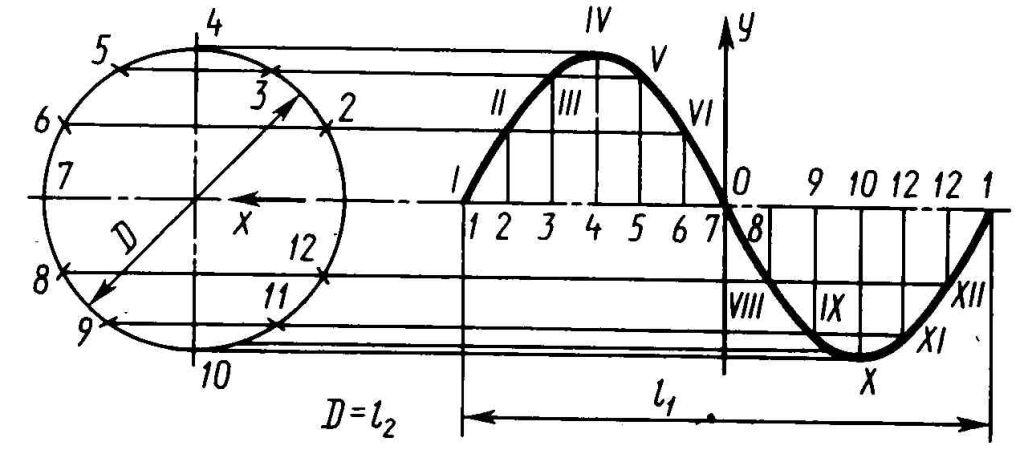
Рис. 7.Построение синусоиды
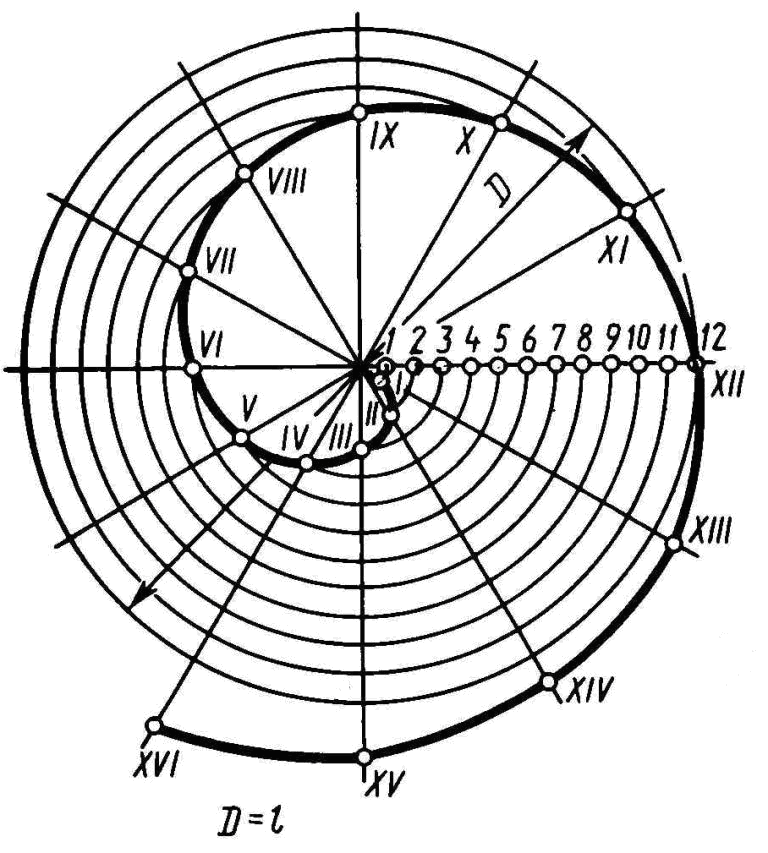
Рис.8 Построение спирали Архимеда
На рис. 7 показан приём построения синусоиды. Заданная окружность разделена на 12 равных частей, на такое же число равных частей делится отрезок прямой, равный длине развёрнутой окружности (l1). Проведя через точки деления горизонтальные и вертикальные прямые, находят в их пересечении точки синусоиды.
На рис. 7 показан пример построения спирали Архимеда. Для построения её делят заданную окружность на 12 равных частей, радиус окружности также делим на 12 равных частей. Проводят лучи из центра через точки деления окружности. Откладывают на первом луче одно деление радиуса, на втором – два и т. д., получают ряд точек спирали, которые соединяют с помощью лекала.