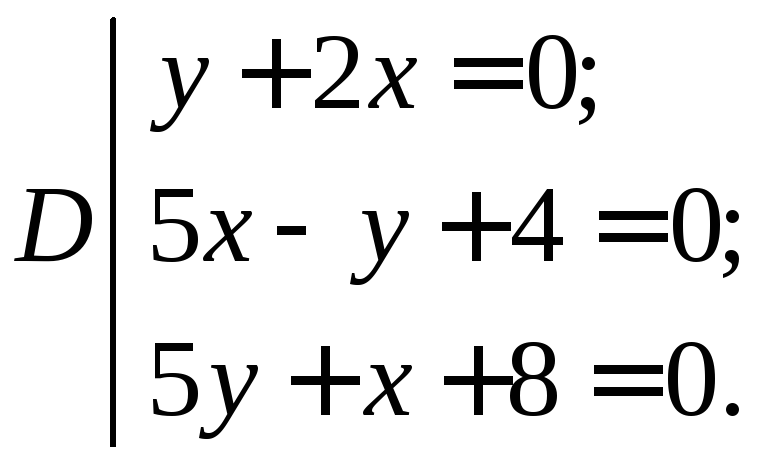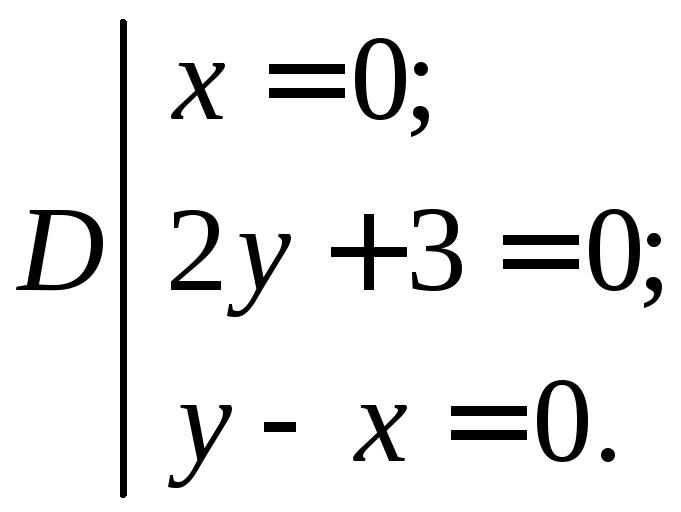Implicitplot(f, a..B, c..D, опции);

Здесь в первой форме вызова команды параметр expr представляет уравнение, зависящее от двух переменных x и y, а во второй форме f представляет уравнение, и в левую, и в правую части которого входят только процедуры-функции и операторы от двух переменных. Дополнительно ко всем известным опциям команды plot() можно задать опцию grid=[m,n], которая определяет сетку из mn точек, на которой вычерчивается кривая. При увеличении количества точек в сетке кривая отображается более гладкой без угловых точек. По умолчанию используется сетка 2525 точек. Опцией coords можно задавать график в разных системах координат, по умолчанию используется декартова прямоугольная система координат.

Пример. График неявно заданной функции

> implicitplot(x^2+y^3-8=0, x=-10..10, y=-8..8,

color=black, grid=[60,60], thickness=2);

Замечание. Увеличение числа точек в сетке, на которой рассчитывается неявно заданная кривая, приводит к существенному увеличению времени расчета её графика.

ЗАДАНИЯ. 1. Нарисовать эллипсы , предварительно задав полуосиа и b. В первом случае сделайте , во втором, в третьем.

2. Нарисовать гиперболу с выводом заданныха и b. На том же графике пунктиром изобразить асимптоты . Точками изобразить прямоугольник гиперболы.

3. Нарисовать параболы с их директрисами. Параметрр принять равным 4.

4. Получите область, ограниченную прямыми. Во втором примере число π задавать как . Сделайте свой вариант. Если область не получается, внесите изменения в уравнения.

4. Задайте уравнение двух любых прямых в отрезках и постройте их.

1.	2.	3.	4.
5.	6.	7.	8.
9.	10.	11.	12.
13.	14.	15.	16.

10. Команда polygonplot() строит на плоскости один или несколько многоугольников, заданных своими вершинами. Каждый многоугольник задается в виде списка координат его вершин, представленных в форме двухэлементных списков. В случае отображения нескольких многоугольников они задаются либо списком, либо множеством.

Пример 9. Отображение многоугольников

> one_poly := [[0.5,0],[0.5,1],[1,1] ,[1,0]];

> ngon := n -> [seq([cos(2*Pi*i/n), sin(2*Pi*i/n) ], i = 1..n)];

> polygonplot([one_poly, ngon(10)],color=grey, thickness=3,

scaling=CONSTRAINED);

ЗАДАНИЕ. Построить произвольные четырёхугольник и пятиугольник. С помощью процедуры ngon( ) построить правильные многоугольники разного цвета с числом сторон от 3 до 8.

12. Отображение текста. Align – выравнивание. Higher – выше, righter – правее, lower – ниже, lefter – левее.

Пример 12. Отображение текста

> t1:=textplot([1,2," higher & righter"], align={ABOVE,RIGHT}, color=magenta):

> t2:=textplot([1,2," higher & lefter "], align={ABOVE,LEFT}, color=blue):

> t3:=textplot([1,2," lower & lefter "], align={BELOW,LEFT}, color=red):

> t4:=textplot([1,2," lower & righter"], align={BELOW,RIGHT}, color=green):

> f:=plot([[1,2]],style=POINT,color=black,symbolsize=10):

> display([t1, t2, t3, t4, f]);

Для совмещения на одном рисунке примера 13 выводов нескольких графических команд использована команда display(). Переменным t1, t2, t3, t4, f присваиваются значения графиков.

ЗАДАНИЯ. 1. Получить отображение, заданное приведёнными выше командами.

2. Написать команды для получения отображения, показанного на рисунке.

3. Составить другие тексты и отобразить их на рисунке.