ЛАБ MAPLE ИС / лаб 11-1 интересные геом тела

ЛАБОРАТОРНАЯ РАБОТА № 8-3

Интересные геометрические тела

1. >

>

>

2. Звёздчатый икосаэдр, форма 22

> with(geom3d):

Warning, the name polar has been redefined

Зададим 22-ю звёздчатую форму икосаэдра с центром в точке (1,1,1), радиуса 2.

> stellate(i1,icosahedron(i,point(o,1,1,1),2),22);

> coordinates(center(i1));

> form(i1);

> schlafli(i1);

Plotting:

> draw(i1,style=patch,orientation=[-90,145],lightmodel=light4,

title=`stellated icosahedron - 22`);

3. Звёздчатый икосаэдр, форма 46 (пересечение пяти тетраэдров)

> stellate(sico,icosahedron(ico,point(o,0,0,0),1),46);

> IsStellated(sico);

Plotting:

> draw(sico,style=patch,lightmodel=light4,shading=XY,orientation=[-142,-127],

title=`stellated icosahedron - 46`);

Найдите все 5 тетраэдров, которые пересекаются в пространстве.

4. ОРИЕНТИРУЕМЫЕ И НЕОРИЕНТИРУЕМЫЕ ПОВЕРХНОСТИ

1. Пример ориентирумой поверхности: тор (построить)

2. Неориентирумая поверхность – лента Мёбиуса.

3. Неориентирумая поверхность – бутылка Клейна.

2. Лента Мёбиуса.

>

> >

>

>

>

>

>

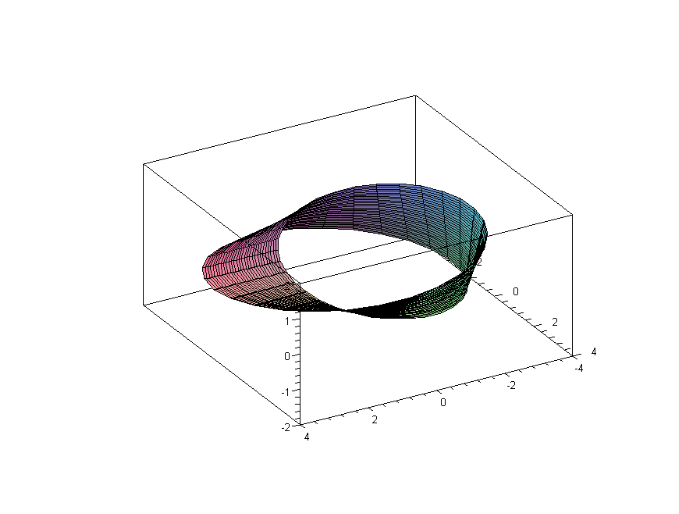
Построим касательные векторы к ленте Мёбиуса:

>

>

Найдём их векторное произведение, это будет нормаль:

>

Найдём длину этого вектора с помощью скалярного произведения:

Вычислим единичный вектор нормали:

>

>

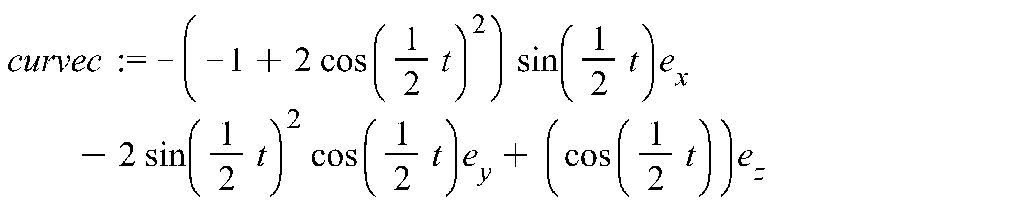
_{Составляем последовательность нормалей к поверхности:}

_{Отображаем все нормали:}

Рисуем ленту Мёбиуса вместе с нормалями:

3. Бутылка Клейна - это интересная поверхность, которая не имеет ни внутренности, ни внешности. Это означает, что она не ориентируема. Можно изобразить различные "иммерсии" (погружения) в бутылку Клейна. Хотя эта поверхность не имеет самопересечений, в трёхмерном Эвклидовом пространстве заметить это невозможно. Двумерные сечения бутылки Клейна в 3-мерном Эвклидовом пространстве называются иммерсиями (immersions). "Обычная" иммерсия бутылки Клейна имеет параметризацию r(u,v)=x(u,v)i+y(u,v)j+z(u,v)k, где

,

,

.

>

>

>

>

>

На этом рисунке невозможно увидеть, что бутылка Клейна не имеет ни внутренней, ни внешней поверхности. Построим другую иммерсию (Figure-8 immersion). Её параметризация имеет вид:

Построим эту поверхность при с=3.

Найдём нормали к поверхности по формуле . Reversing path– меняющий направление путь. Зададим путь формулой

.

Он начинается и заканчивается при .

Компоненты r и n вычисляются в Maple.

Ещё один способ построения бутылки Клейна:

8