3.5. Эффективные алгоритмы вычисления степеней

3.5.1. Бинарный метод

С целью сокращения операций умножения целесообразно по возможности часто использовать в промежуточных вычислениях возведение в квадрат: вместо цепочки действий при вычислении вида

можно провести вычисления по схеме

.

Если показатель не является степенью двойки, помимо возведений в квадрат приходится иногда производить умножение на. Например, при вычислении:

.

Последовательность возведений в квадрат и умножений может быть и другой. Например, после вычисления можно дальше вычислять

.

Если не запоминать отдельно результаты промежуточных вычислений, то на каждом шаге мы имеем только исходное число и его очередную степень. Стандартную последовательность действий можно получить исходя из двоичной записи показателя степениследующим образом.

В двоичной записи:

; ;

; ;

; ;

; .

; .

Порядок возведений в квадрат и умножений на первую степень не зависит от старшей цифры двоичного представления показателя, которая всегда равна единице. Далее, при сканировании представления слева направо, очередной цифресоответствует возведение уже накопленного результата в квадрат, а очередной цифресоответствует возведение в квадрат и умножение на первую степень исходного основания.

Данное правило соответствует представлению показателя в виде

При возведении в степень по заданному модулю , то есть при вычисленииследует каждый промежуточный результат заменять остатком от деления на. Это позволяет оперировать с числами в существенно меньшем диапазоне:

…

поскольку , то

….

3.5.2. Метод факторизации показателя

Пусть составной показатель разложен в произведение с участием своего простого множителя:. Вычисление степени может быть проведено по схеме.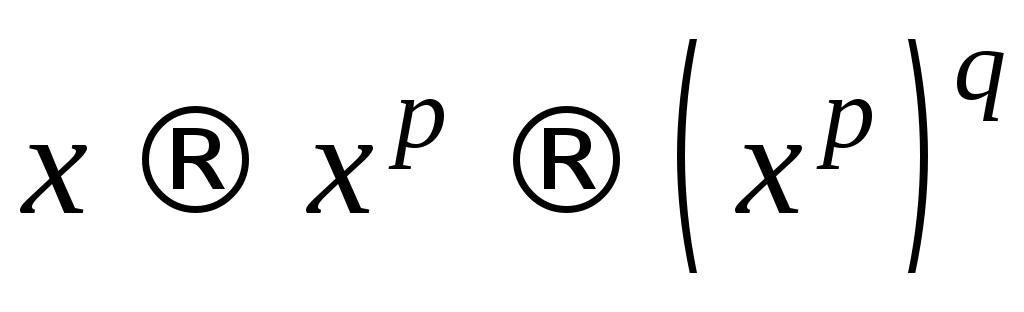

Например, , где сначала вычисляетсяпо схеме, изложенной выше:

,

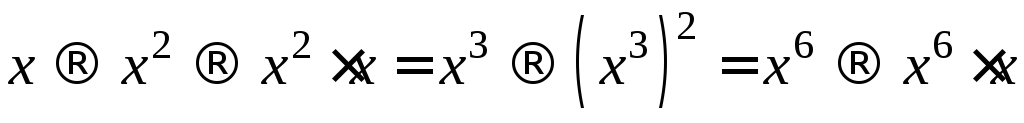а затем по той же схеме вычисляется .

3.6. Эффективные действия с дробями

Дробь может быть представлена как упорядоченная пара чисел (первое число — числитель, второе — знаменатель). Для экономного представления естественно потребовать взаимную простотуи.

Умножение дробей, производимое по схеме

может нарушить взаимную простоту числителя и знаменателя для их произведения. Поэтому сначала находятся с помощью алгоритма Евклида наибольшие общие делители ,

так что

,

и

,

где целые числа находятся предварительно делением «в столбик» (с нулевым остатком). Другой возможностью является отыскание наибольшего общего делителяи деление на него числителяи знаменателярезультирующей дроби. Второй случай, однако, приводит к действиям с бóльшими числами

Деление дробей соответствует схеме

,

и также предполагает обеспечение взаимной простоты числителя и знаменателя результирующей дроби одним из двух способов аналогично случаю произведения дробей.

Сложение и вычитание дробей соответствует схеме

,

после чего дробь приводится к несократимому виду после отыскания наибольшего общего делителя числителя и знаменателя результирующей дроби. Можно также предварительно найти и выполнить сложение/вычитание дробей с меньшими числами:

. Пусть и, так что . Тогда, где могут оказаться существенно меньше исходных, и можно показать, что дробь несократима.