3.2. Арифметика чисел с фиксированной точкой

Выполнение арифметических действий с числами в форме с фиксированной точкой осуществляется быстрее и проще, чем в случае представления с естественной точкой. По сути, алгоритмы этих операций такие же, как при операциях с целыми числами (без дробной части).

При выполнении арифметических действий возможно переполнение отведённой разрядной сетки, рассматриваемое как аварийная ситуация.

Машинное умножение целых чисел. В -ичной системе счисления умножение целого числана целое числореализуется согласно равенству

.

Машинное умножение целых чисел основано на этом равенстве: частичное произведение реализуется последовательностью операций сложения:

;

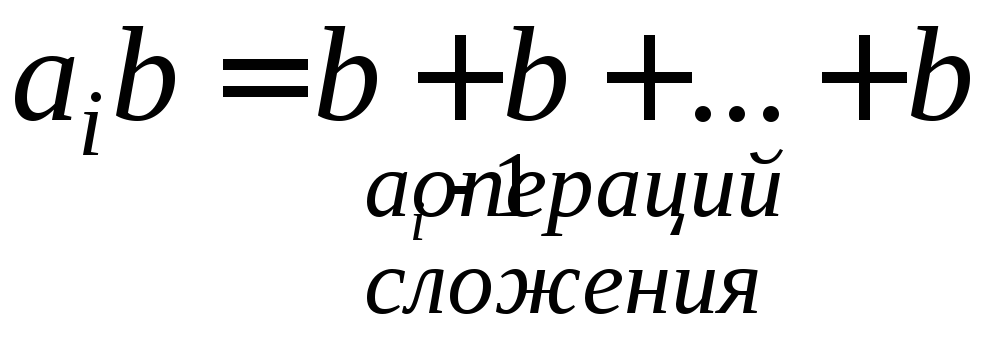после этого умножение на степень основания системы счисления осуществляется как сдвиг на разрядов влево по разрядной сетке с дописыванием нулей справа; затем складываются полученные числа. Итак, машинное умножение целых чисел осуществляется с помощью аппаратно реализованных операций сложения и сдвига.

Машинное деление целых чисел. Алгоритм деления существенно зависит не только от реализованных в компьютере аппаратных средств, но и от кода представления делимого и делителя — прямого, дополнительного или обратного.

Возможный алгоритм деления для чисел, представленных в прямом коде, основан на алгоритме деления с остатком и является формальной алгоритмизацией привычного деления «в столбик», поизводимого «на бумаге» (см. [16], с. 83 и далее).

Важным промежуточным этапом на каждой итерации деления «в столбик» является отыскание неполного частного при делении -разрядного числана-разрядное число (в школе это учат делать «подбором»).

Например, при делении 3157 на 59 с остатком сначала , так что неполное частное, остаток. На следующем шаге к остаткудописывается следующая цифраделителя, что означает деление начисла(в общем случае при основании системы счисленияделится).

Подбор может осуществляться циклической процедурой последовательного вычитания-разрядного делителя из-разрядного очередного остаткавплоть до получения отрицательной разности. Более прямой метод, использующий старшие разрядыи делителя, описан у Кнута ([8], с. 310 и далее).

3.3. Арифметика чисел с плавающей точкой

3.3.1. Представление чисел в форме с плавающей точкой. Запись числа в форме с плавающей точкой (или с плавающей запятой) имеет вид

, (28)

где — основание системы счисления (обычно, реже),—мантисса (или дробная часть), удовлетворяющая неравенству ,— целое число со знаком, называемоепорядком.

Для представления мантиссы и порядка отводится машинное слово с фиксированным (для конкретного типа компьютеров) числом -ичных разрядов:разрядов для мантиссы, разрядов для порядка.

Представление (28) называется нормализованным, если старшая цифра мантиссы отлична от нуля, что равносильно условию

.

Пример. Записи иявляются ненормализованными представлениями числа, а запись— нормализованным представлением.

Если для представления модуля мантиссы отводится разрядов, то в случае нормализованного представления

.

Замечание. Нормализованность представления может определяться и по-другому для разных типов компьютеров. При этом по умолчанию подразумеваются те или иные соглашения.

Сравнение положительных нормализованных чисел по величине сводится к сравнению их порядков, и лишь при равенстве порядков — к сравнению мантисс:

.

Дискретность множества чисел с плавающей точкой обусловлена конечностью множества представляемых чисел (машинных чисел) при фиксированном количестве -ичных разрядов для мантиссы и для порядка. Отсюда вытекает существование наименьшего (ближайшего к нулю) положительного машинного числа. Это число(машинное эпсилон) представляется мантиссой, содержащей единицу в старшем разряде (требование нормализованности) и нули в остальных разрядах и минимально возможным при данной разрядности отрицательном порядке :

.

Сетка машинных чисел с плавающей точкой меняется с ростом порядка: числа с малыми порядками расположены гуще, числа с большими порядками — реже. Наибольшее машинное число имеет мантиссу, состоящую из старших цифр -ичной системы (из единиц для двоичной системы, из девяток для десятичной), и максимально возможный порядок.

Свойства арифметических операций. Дискретность множества машинных чисел приводит к тому, что арифметические операции с ними выполняются лишь приближённо, так что для них вводятся новые обозначения, например, с точкой: вместо стандартных символов.

Для этих новых операций уже могут не выполняться привычные законы арифметических действий, прежде всего законы ассоциативности: порядок выполнения операций, то есть способ расстановки скобок, может существенно повлиять на результат.