Лабораторная Работа № 6
-
Перегрузка операторов
-
8 неделя
-
Создание и использование перегруженных операторных функций в консольном приложении MS Visual C++ 6.0
-
Правила перегрузки операторов. Перегрузка оператора присваивания. Перегрузка бинарных операторов. Перегрузка бинарных операторов, использующих объекты двух классов. Перегрузка унарных операторов. Перегрузка операторов инкремента и декремента. Перегрузка оператора вызова функции. Перегрузка оператора преобразования типа. Перегрузка операторов X=. Перегрузка оператора индексирования.
-
Общие требования
Составьте программу, которая решает поставленную в вашем варианте задачу. Программа должна:
-
представлять собой консольное приложение;
-
содержать русскоязычный или украинско-язычный интерфейс;
-
исходные данные должны быть заданны в качестве начальных значений переменных (тестовый вариант);
-
содержать ввод исходных данных с клавиатуры (пользовательский вариант);
-
отображать сведения о назначении и возможностях программы;
-
отображать сведения об авторе программы;
-
выводить результаты расчётов на экран;
-
содержать запрос о продолжении работы;
-
содержать в коде необходимые пояснения;
-
программа должна быть протестирована;
Тематические требования
-
содержать несколько классов;
-
каждый класс должен содержать закрытые данные-члены класса;
-
каждый класс должен содержать один или несколько конструкторов;
-
каждый шаг решения задачи должен быть реализован с помощью перегруженного оператора;
-
перегруженные операторные функции быть универсальными (допускать их использование при решении других вариантов лабораторной работы);
-
задача должна быть решена с помощью объявления объектов класса и вызова перегруженных операторных функции.
Индивидуальные задания
|
№ |
Задание |
|
1 |
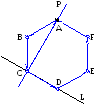
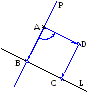
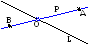
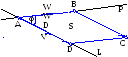
Уголковый отражатель, состоит из двух зеркал расположенных под прямым углом друг к другу. Уголковый отражатель задан уравнением прямой одного зеркала и точкой лежащей на другом зеркале. Луч света распространяется вдоль заданной прямой и последовательно отражается от зеркал уголкового отражателя. Определить уравнение прямой, вдоль которой распространяется отраженный луч. Показать, что падающий и отражённый лучи параллельны. |
|
2 |
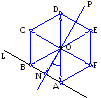
Заданы координаты центра шестиугольника и прямая, на которой лежит его сторона. Определить координаты вершин и площадь шестиугольника. |
|
3 |
Заданы координаты вершины шестиугольника и прямая, на которой лежит его сторона. Определить координаты остальных вершин (два решения) и площадь шестиугольника. |
|
4 |
Заданы координаты вершины шестиугольника и прямая, на которой лежит его сторона. Определить координаты остальных вершин (два решения) и площадь шестиугольника. |
|
5 |
Заданы координаты вершины квадрата и прямая, на которой лежит его сторона. Определить координаты остальных вершин (два решения) и его площадь. |
|
6 |
Заданы координаты центра квадрата и прямая, на которой лежит его сторона. Определить координаты вершин квадрата и его площадь. |
|
7 |
Заданы координаты вершины правильного треугольника и прямая, на которой лежит его сторона. Определить координаты остальных вершин этого треугольника и его площадь |
|
8 |
Заданы координаты центра правильного треугольника и прямая, на которой лежит его сторона. Определить координаты вершин и площадь треугольника |
|
9 |
Заданы координаты вершин основания равнобедренного треугольника и прямая, на которой находится центр тяжести треугольника (точка пересечения его медиан). Определить координаты третьей вершины этого треугольника, его площадь и углы |
|
10 |
Заданы координаты вершины ромба, его площадь и прямая, на которой лежит его диагональ. Определить координаты остальных вершин ромба. |
|
11 |
З
|
|
12 |
Луч света распространяется вдоль заданной прямой и отражается от зеркала, расположенного вдоль другой заданной прямой. Определить уравнение прямой, вдоль которой распространяется отраженный луч. |
|
13 |
Заданы координаты трёх вершин треугольника. Определить координаты центра и радиус описанной вокруг треугольника окружности. |
|
12 |
Заданы координаты трёх вершин треугольника. Определить координаты центра и радиус вписанной в треугольник окружности.
|
|
14 |
Заданы координаты центра прямоугольника, его площадь и прямая, на которой лежит сторона прямоугольника. Определить координаты вершин прямоугольника. |
|
15 |
Заданы координаты вершины прямоугольника, его площадь и прямая, на которой лежит сторона прямоугольника. Определить координаты вершин прямоугольника (два решения). |
|
16 |
Задана площадь прямоугольника и две прямые, на которой лежат сторона прямоугольника его диагональ. Определить координаты вершин прямоугольника (четыре решения). |
|
17 |
Заданы координаты вершины правильного треугольника и прямая, на которой лежит его высота. Определить координаты остальных вершин этого треугольника и его площадь. |
|
18 |
Задана площадь равнобедренного треугольника и две прямые, на которой лежат его боковые стороны. Определить координаты всех вершин треугольника (четыре решения). |
|
19 |
Задана длина основания равнобедренного треугольника и две прямые, на которой лежат его боковые стороны. Определить координаты всех вершин треугольника (четыре решения). |
|
20 |
Задана площадь прямоугольника и две прямые, на которой лежат его диагонали. Определить координаты вершин прямоугольника и уравнения его сторон. |
|
21 |
Задана длина стороны прямоугольника и две прямые, на которой лежат его диагонали. Определить координаты вершин прямоугольника (два решения), площадь прямоугольника и уравнения его сторон. |
|
22 |
Заданы координаты вершины параллелограмма и две прямые, на которых лежат его стороны. Определить площадь параллелограмма, координаты остальных вершин и точки пересечения его диагоналей. |
|
23 |
Заданы три прямых, образующих треугольник. Определить координаты вершин, площадь и углы этого треугольника. |
|
24 |
Заданы координаты вершины равностороннего прямоугольного треугольника и прямая, на которой лежит его гипотенуза. Определить координаты остальных вершин треугольника и его площадь. |
|
25 |
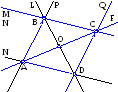
Заданы три прямые, на которых лежат две стороны и диагональ параллелограмма. Определить координаты вершин, точки пересечения диагоналей, площадь, и углы этого параллелограмма. |
|
26 |
Задана площадь ромба и две прямые, на которой лежат его стороны. Определить координаты всех вершин ромба (четыре решения). |
|
27 |
З |
|
28 |
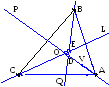
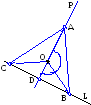
Заданы координаты вершин треугольника. Определить уравнения биссектрис углов треугольника и точку их пересечения. Показать что, все биссектрисы углов треугольника пересекаются в одной точке. |
|
29 |
Заданы координаты вершин треугольника. Определить уравнения его высот и точку их пересечения. Показать что, все высоты пересекаются в одной точке. |
|
30 |
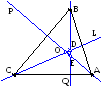
Заданы координаты вершин треугольника. Определить уравнения прямых, перпендикулярных сторонам треугольника и проходящих через их середины. Показать что, все эти прямые пересекаются в одной точке. |





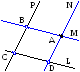
 аданы
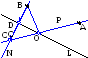
координаты двух точек и прямая. Найти
точку, лежащую на прямой и равноудалённую
от двух заданных точек.
аданы
координаты двух точек и прямая. Найти
точку, лежащую на прямой и равноудалённую
от двух заданных точек.
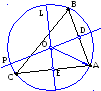

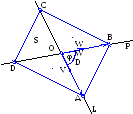
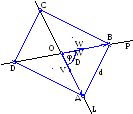


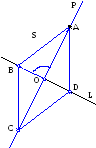
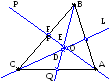 аданы
координаты вершин треугольника.
Определить уравнения его медиан и
точку их пересечения. Показать что,
все медианы пересекаются в одной
точке.
аданы
координаты вершин треугольника.
Определить уравнения его медиан и
точку их пересечения. Показать что,
все медианы пересекаются в одной
точке.