Лабораторна робота №2

Тема:Чисельні методи розв’язання нелінійних рівнянь з однією змінною.

Мета:Вивчити можливості табличних процесорів MS Excel для розв’язання нелінійних рівнянь з однією змінною, використовуючи чисельні методи.

Завдання:

1. Вивчити інтервали ізоляції коренів рівняння.

2. Уточнити один з дійсних коренів рівняння, використовуючи:

• Метод ділення відрізку навпіл;

• Метод хорд;

• Метод дотичних;

• Вбудований інструмент електронних таблиць «Подбор параметра».

3. Порівняти отримані результати та зробити висновки.

Метод поділу відрізка навпіл

Метод поділу відрізка пополам (або метод дихотомії) застосовний для уточнення кореня рівняння f(x)=0 з наперед заданою точністю.

Нехай на проміжку [а; b] функція f(x) неперервна і набуває на кінцях проміжку значень різних знаків, тобто f (а) • f (b) < 0. Це означає, що на [а; b] рівняння f(x)=0 має принаймні один корінь. Цей корінь можна визначити з наперед заданою точністю методом поділу відрізка пополам.

Суть методу полягає в тому, що відрізок, на якому міститься корінь, поступово звужують, зменшуючи його щоразу вдвоє, поки не досягнуть потрібної точності визначення кореня.

Позначимо лівий кінець відрізка, на яко-

мал.1

му міститься корінь, буквою u₀ (а=u₀), правий – буквою v₀ (b=v₀) і знайдемо середину цього відрізка: с =. Оскільки (за умовою) f(u₀)f(v₀)<0, то f(a)f(с)>0, або f(с)f(в)<0, або f(с) = 0. Якщо f(с)= 0, то корінь х* = с (мал. 1).

Зрозуміло, що у випадку f(a)f(с)>0 корінь міститься на відрізку [c; v₀]. У випадку f(а)f(c) < 0 корінь міститься на відрізку [u₀; c].

Якщо довжина відрізка, на якому міститься корінь, не перевищує заданої величини , то це означає, що х* знайдено з точністю до , бо

|с-х*|с-u₀.

Якщо заданої точності ще не досягнуто, то, позначивши с через u₀ у випадку f(a)f(с)>0 або через v₀ у випадку f(а)f(с)<0, знову зна­ходимо середину відрізку [u₀; v₀] і повторюємо обчислення.

Переконатися в тому, що потрібна точність при обчисленні кореня х* уже досягнута, можна й іншим способом. Якщо на деякому відрізку [а; b] функція f(х) диференційована і 0‹m|f’(x)| (у цьому випадку на [а; b] міститься єдиний корінь рівняння f(х)=0) і якщо , (1)

то можна вважати, що х – наближене значення кореня х* з точністю до.

Дійсно, за теоремою про середнє маємо:

|f(x)-f(х*)|=|(x- х*)| (x‹‹ х*, або х*‹‹ х).

Враховуючи, що f(х*)=0, дістанемо:

|x-х*|= , де m.

Умову (1) можна вико­ристати для перевірки близь­кості х до х*, якщо х знайде­но будь-яким способом, а не тільки методом ділення відрізку пополам.

Зауважимо, що близькість до нуля f(х) не означає близькості х до х* (мал.2).

Послідовність наближень, знайдених методом поділу про­міжку пополам, збігається до кореня х* рівняння f(х)=0, причому щоразу маємо для х* оцінки знизу і зверху: и₀ ≤ х*≤ v₀.

При обчисленні значень f(х) достатньо мати одну-дві пра­вильні значущі цифри, оскільки нас цікавить лише знак f(х) при даному х.

МЕТОД ХОРД

Метод хорд — один з поширених ітераційних методів. Його ще називають методом лінійного інтерполювання, методом пропорційних частин, або методом хибного положення.

Нехай задано рівняння , де на відрізку має непе­рервні похідні першого й другого порядків, які зберігають сталі знаки на цьому відрізку, і, тобто корінь рівняння відокремлений на .

Ідея методу хорд в тому, що на досить малому відрізку дуга кривої замінюється хордою і абсциса точки перетину хорди з віссю є наближеним значенням кореня.

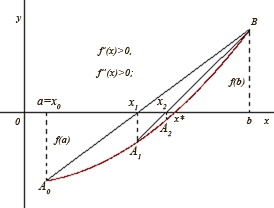
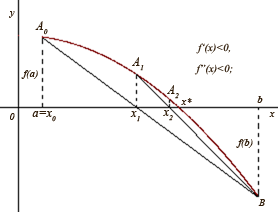
а б

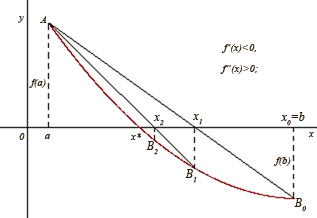
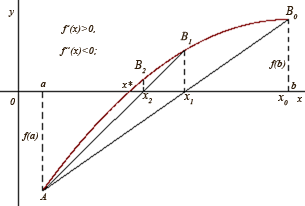
в г

рис.1

Нехай для визначеності, , , (рис. 1, а). Візьмемо за початкове наближення шуканого кореня значення . Через точки і проведемо хорду і за перше наближення кореня візьмемо абсцису точки перетину хорди з віссю . Тепер наближене значення кореня можна уточнити, якщо застосувати метод хорд до відрізка . Абсциса точки перетину хорди буде другим наближенням кореня. Продовжуючи цей процес необмежено, дістанемо послідовність наближених значень кореня даного рівняння.

Для виведення формули методу хорд запишемо рівняння прямої, що проходить через точки і :

.

Поклавши , знайдемо абсцису точки перетину хорди з віссю : .

Значення можна взяти за наступне наближення, тобто

, тобто = 0,1,2,... .

У цьому разі і тоді, коли , , , (рис. 1, б) кінець відрізка є нерухомим.

Якщо , , , (рис. 1, в), або , , , (рис. 1, г), аналогічно можна записати формулу:

, тобто = 0,1,2,... .

У цьому випадку точка є нерухомим кінцем відрізка .

У загальному випадку нерухомим буде той кінець відрізка ізоляції кореня, в якому знак функції збігається із знаком другої похідної, а за початкове наближення можна взяти точку відрізка , в якій .

Отже, метод хорд можна записати так:

, тобто = 0,1,2,.... (1)

де

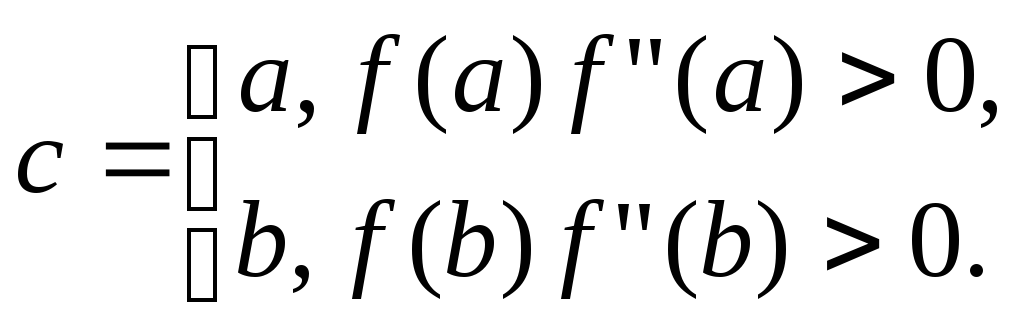
З формули (1) видно, що метод хорд є методом ітерацій , в якому

(2)

Зауважимо, що рівняння

на відрізку рівносильне рівнянню .

Достатні умови збіжності методу хорд дає така теорема.