- •Кафедра инженерной графики и механики
- •Введение
- •1. Порядок выбора вариантов и оформления расчетно-графических работ
- •2. Задача 1. «Сложное движение точки»
- •3. Задача 2. « Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил»
- •4. Задача 3. «Применение теоремы об изменении кинетического момента к определению угловой скорости твердого тела»
- •5. Задача 4. «Применение теоремы об изменении кинетической энергии к изучению движения механической системы»
3. Задача 2. « Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил»
Варианты 1 – 5
(схема 1). Тело движется из точки А по
участку АВ
(длиной
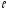 )
по наклонной плоскости, составляющей
угол
)
по наклонной плоскости, составляющей
угол с горизонтом, в течение
с горизонтом, в течение с. Его начальная скорость
с. Его начальная скорость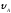 .
Коэффициент
трения
скольжения тела по плоскости равен
.
Коэффициент
трения
скольжения тела по плоскости равен
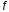 .
.
В точке В
тело покидает
плоскость со скоростью
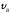 и попадает со скоростью
и попадает со скоростью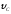 в точку С
плоскости BD,
наклоненной
под углом
в точку С
плоскости BD,
наклоненной
под углом
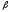 к горизонту, находясь в воздухеТ
с.
к горизонту, находясь в воздухеТ
с.
При решении задачи тело принять за материальную точку; сопротивление воздуха не учитывать.
Вариант 1. Дано:
 = 30°;
= 30°;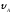 =
0 ,
=
0 ,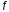 =
0,2
=
0,2
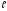 =
10м ,
=
10м ,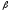 =60°.
Определить
=60°.
Определить и
и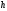
Вариант 2. Дано:
 = 15°;
= 15°;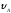 =
2м/с,
=
2м/с,
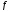 =
0,2 ,
=
0,2 ,
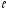 =
4м,
=
4м,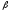 =45°.
Определить
=45°.
Определить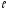 и уравнение траектории точки на участкеBC.
и уравнение траектории точки на участкеBC.
Вариант 3. Дано:
 = 30°;
= 30°;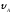 =2,5м/с
,
=2,5м/с
,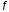 ≠
0 , ,
≠
0 , ,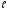 =
8м ,d
= 10м,
=
8м ,d
= 10м,
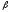 =60°.
Определить
=60°.
Определить и
и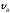
Вариант 4. Дано:
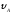 =0,
=0,
 =
2с,
=
2с,
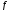 =
0;
=
0;
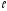 =9,8м;
=9,8м;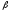 =60°.
Определить
=60°.
Определить иT.
иT.
Вариант 5. Дано:
 = 30°;
= 30°;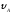 =
0,
=
0,
 =
3с,
=
3с,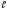 =9,8м;
=9,8м;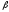 =45°.
Определить
=45°.
Определить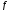 и
и
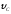
Варианты 6 - 10 (схема 2). Лыжник подходи к точке А участка трамплина
АВ, наклоненного
под углом
 к горизонту и имеющего длину
к горизонту и имеющего длину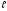 , со скоростью
, со скоростью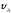 .
.
Коэффициент трения
скольжения лыж на участке АВ
равен
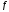 .
Лыжник отА
до В движется
.
Лыжник отА
до В движется
 с; в точкеB
со скоростью
с; в точкеB
со скоростью
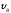 он покидает трамплин. Через Т с лыжник
приземляется со скоростью
он покидает трамплин. Через Т с лыжник
приземляется со скоростью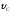 в точке С горы, составляющей угол
в точке С горы, составляющей угол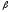 с горизонтом
с горизонтом
При решении задачи принять лыжника за материальную точку и не учитывать сопротивление воздуха.
Вариант 6. Дано:
 = 20°,
= 20°,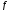 =
0,1,
=
0,1,
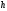 = 40м ,
= 40м ,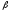 =30°.
=30°.
Определить
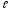 и
и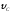
Вариант 7. Дано:
 = 15°;
= 15°;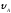 =
16 м/с ,
=
16 м/с ,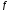 =
0,1
=
0,1
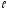 =
5м ,
=
5м ,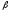 =45°.
=45°.
Определить
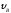 иT.
иT.
Вариант 8. Дано:
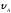 =
21м/с ,
=
21м/с ,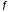 =
0,
=
0,
 =
3с,
=
3с,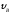 =
20м/с ,
=
20м/с ,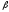 =60°.
=60°.
Определить
 иd
иd
Вариант 9 Дано:
 = 15°;
= 15°; =
3с,
=
3с,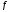 =
0,1,
=
0,1,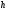 =
=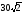 м
,
м
,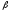 =45°.
Определить
=45°.
Определить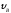 и
и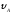 .
.
Вариант 10. Дано:
 = 15°;
= 15°;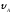 =
12м/с ,
=
12м/с ,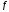 =
0, d
= 50м ,
=
0, d
= 50м ,
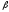 =60°.
Определить
=60°.
Определить и уравнение траектории лыжника на
участкеBC.
и уравнение траектории лыжника на
участкеBC.
Варианты 11 – 15
(схема 3). Имея в точке А
скорость
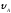 ,
мотоцикл
поднимается
,
мотоцикл
поднимается
 с по участкуАВ
длиной
с по участкуАВ
длиной
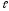 ,
составляющему с горизонтом угол
,
составляющему с горизонтом угол .
При постоянной на всем участкеАВ
движущей
силе Р мотоцикл
в точке В
приобретает
скорость
.
При постоянной на всем участкеАВ
движущей
силе Р мотоцикл
в точке В
приобретает
скорость
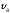 и перелетает
через ров шириной d,
находясь в
воздухе Тс и приземляясь в точке С со
скоростью
и перелетает
через ров шириной d,
находясь в
воздухе Тс и приземляясь в точке С со
скоростью
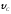 .
Масса
мотоцикла с мотоциклистом равна т.
.
Масса
мотоцикла с мотоциклистом равна т.
При решении задачи считать мотоцикл с мотоциклистом материальной точкой и не учитывать силы сопротивления движению.
Вариант 11. Дано:
 = 30°;Р ≠ 0;
= 30°;Р ≠ 0;
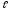 = 40 м;
= 40 м;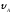 = 0:
= 0: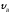 = 4,5 м/с; d
= 3 м. Определить
= 4,5 м/с; d
= 3 м. Определить
 и
и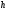 .
.
Вариант 12. Дано:
 = 30°;Р =
0;
= 30°;Р =
0;
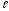 = 40 м;
= 40 м;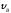 = 4,5 м/с;
= 4,5 м/с;
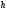 = 1,5 м. Определить
= 1,5 м. Определить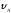 и d.
и d.
Вариант 13. Дано:
 = 30°; т
= 400 кг,
= 30°; т
= 400 кг,
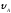 = 0;
= 0;
 = 20 с;d
= 3 м;
= 20 с;d
= 3 м;
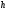 =1,5 м. ОпределитьР
и
=1,5 м. ОпределитьР
и
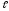 .
.
Вариант 14. Дано:
 = 30°;т =
400 кг; Р
= 2,2 кН;
= 30°;т =
400 кг; Р
= 2,2 кН;
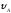 = 0;
= 0;
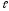 =
40 м; :d
= 5 м. Определить
=
40 м; :d
= 5 м. Определить
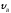 и
и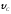 .
.
Вариант 15. Дано:
 = 30°;
= 30°;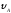 =
0; Р = 2 кН,
=
0; Р = 2 кН,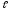 = 50 м;
= 50 м;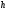 =50 м, d
= 4 м. Определить
Т и
т
=50 м, d
= 4 м. Определить
Т и
т
Варианты 16 – 20
(схема 4). Камень скользит в течение
 с , по участкуАВ
откоса,
составляющему угол
с , по участкуАВ
откоса,
составляющему угол
 с горизонтом
и имеющему длину
с горизонтом
и имеющему длину
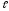 .
Его начальная скорость
.
Его начальная скорость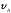 .
Коэффициент
трения скольжения камня по откосу равен
.
Коэффициент
трения скольжения камня по откосу равен
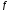 Имея в точкеВ
скорость
Имея в точкеВ
скорость
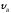 ,
камень через
Т с ударяется ; в точке С о вертикальную
защитную стену.
,
камень через
Т с ударяется ; в точке С о вертикальную
защитную стену.
При решении задачи принять камень за материальную точку; сопротивление воздуха не учитывать.
Вариант 16. Дано:
 = 30°;
= 30°;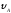 = 1 м/с;
= 1 м/с;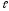 = 3 м;
= 3 м;
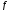 =
0,2; d
= 2,5 м.
Определить
=
0,2; d
= 2,5 м.
Определить
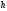 иТ.
иТ.
Вариант 17. Дано:
 = 45°;
= 45°;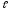 = 6 м;
= 6 м;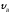 = 2
= 2
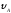 ;
;
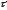 = 1 с;
= 1 с;
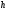 = 6 м. Определитьd
и
f.
= 6 м. Определитьd
и
f.
Вариант 18. Дано:
 = 30°;
= 30°;
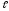 = 2 м;
= 2 м;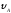 = 0 м/с,
= 0 м/с,
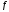 =
0,2; d
= 3 м,
=
0,2; d
= 3 м,
Определить
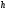 и
и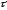 .
.
Вариант 19. Дано:
 = 15°;
= 15°;
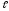 =3 м;
=3 м;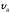 = 3 м/с,
= 3 м/с,
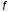 ≠
0;
≠
0;
 = 1,5 с;d
= 2 м,
= 1,5 с;d
= 2 м,
Определить
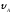 и
и
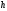 .
.
Вариант 20. Дано:
 = 45°,
= 45°,
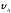 = 0;
= 0;
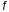 =
0,3;d
= 2 м;
=
0,3;d
= 2 м;
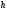 = 4 м. Определить
= 4 м. Определить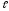 и
и .
.
Варианты 21 – 25
(схема 5).
Тело движется из точки А
по, участку
АВ (длиной
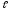 )
наклонной плоскости, составляющей угол
)
наклонной плоскости, составляющей угол с горизонтом. Его начальная скорость
с горизонтом. Его начальная скорость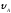 .
Коэффициент
трения скольжения равен
.
Коэффициент
трения скольжения равен
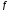 .Через
.Через с тело в точкеВ
со скоростью
с тело в точкеВ
со скоростью
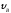 покидает
наклонную плоскость и падает на
горизонтальную плоскость в точку С
со скоростью
покидает
наклонную плоскость и падает на
горизонтальную плоскость в точку С
со скоростью
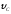 ,
при этом оно
находится в воздухе Т
с.
,
при этом оно
находится в воздухе Т
с.
При решении задачи принять тело за материальную точку и не учитывать сопротивление воздуха.
Вариант 21. Дано:
 = 30°;
= 30°;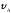 = 1 м/с;
= 1 м/с;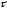 = 1,5 с;
= 1,5 с;
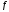 =
0,1;
=
0,1;
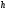 = 10 м. Определить
= 10 м. Определить
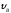 иd.
иd.
Вариант 22. Дано:
 = 45°;
= 45°;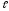 = 10 м;
= 10 м;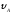 =
0;
=
0;
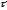 = 2 с; .Определить
= 2 с; .Определить
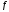 и
уравнение
траектории на участке BC.
и
уравнение
траектории на участке BC.
Вариант 23. Дано:
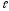 = 9,81 м;
= 9,81 м;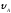 = 0 м/с,
= 0 м/с,
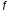 =
0;
=
0;
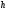 = 20 м,
= 20 м,
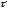 = 2 с, Определить
= 2 с, Определить иT
иT
Вариант 24. Дано:
 = 30°;
= 30°;
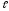 =10 м;
=10 м;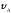 = 0 м/с,
= 0 м/с,
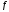 =
0,2; d
= 12 м,
=
0,2; d
= 12 м,
Определить
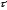 и
и
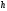 .
.
Вариант 25. Дано:
 = 30°,
= 30°,
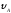 = 0;
= 0;
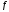 =
0,2;
=
0,2;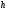 = 4,5 м;
= 4,5 м;
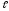 = 6 м. Определить
= 6 м. Определить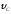 и
и .
.
Варианты 26 – 30
(схема 6). Имея в точке А
скорость
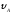 ,тело
движется по горизонтальному
участку АВ
длиной
,тело
движется по горизонтальному
участку АВ
длиной
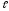 в течение
в течение с. Коэффициент
скольжения тела по плоскости равен
с. Коэффициент
скольжения тела по плоскости равен
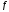 .
Со скоростью
.
Со скоростью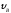 тело в точкеB
покидает плоскость и попадает в точку
С со скоростью
тело в точкеB
покидает плоскость и попадает в точку
С со скоростью
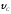 ,
находясь в воздухеT
с. При решении задачи принять тело за
материальную точку; сопротивление
воздуха не учитывать.
,
находясь в воздухеT
с. При решении задачи принять тело за
материальную точку; сопротивление
воздуха не учитывать.
Вариант 26. Дано:
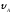 = 7 м/с;
= 7 м/с;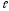 = 8 м,
= 8 м,
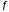 =
0,2;
=
0,2;
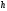 = 20 м.
= 20 м.
Определить
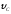 иd.
иd.
Вариант 27. Дано: d
= 2 м;
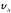 =
4 м/с;
=
4 м/с;
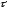 = 2 с;
= 2 с;
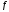 =
0,1 .
=
0,1 .
Определить
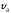 и
и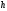 .
.
Вариант 28. Дано:
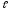 = 3 м;
= 3 м;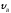 =3
м/с,
=3
м/с,
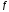 =
0,3;
=
0,3;
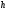 = 5 м.
= 5 м.
Определить
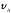 иT
иT
Вариант 29. Дано:
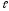 =2,5 м;
=2,5 м;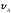 = 3 м/с,
= 3 м/с,
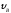 =1
м/с,
=1
м/с,
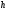 = 20 м.
= 20 м.
Определить
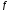 и d.
и d.
Вариант 30. Дано:
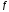 =
0,25;
=
0,25; = 5 м;
= 5 м;
 = 4 м,d
= 3 м.
= 4 м,d
= 3 м.
Определить
 и
и .
.
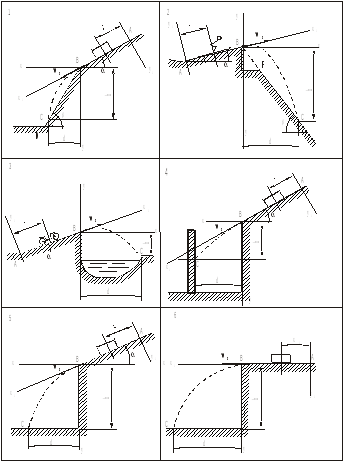
Пример решения Задачи 2
В железнодорожных
скальных выемках кюветов от попадания
в них с откосов каменных осыпей
устанавливается «полка» DC.
Учитывая
возможность движения камня из наивысшей
точки А откоса
и полагая при этом его начальную скорость
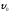 =
0, определить наименьшую ширину полкиb
и скорость
=
0, определить наименьшую ширину полкиb
и скорость
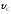 ,
с которой
камень падает на нее. По участку АВ
откоса,
составляющему угол α с горизонтом и
имеющему длину
,
с которой
камень падает на нее. По участку АВ
откоса,
составляющему угол α с горизонтом и
имеющему длину
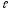 ,
камень движется
,
камень движется с. При решении задачи считать коэффициент
трения скольжения
с. При решении задачи считать коэффициент
трения скольжения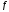 камня на участкеAB
постоянным, а сопротивлением воздуха
пренебречь.
камня на участкеAB
постоянным, а сопротивлением воздуха
пренебречь.
Дано:
 = 60°;
= 60°;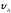 =0 м/с
,
=0 м/с
,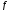 ≠
0 ,
≠
0 ,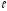 =
4м ,
=
4м , = 1 с,
= 1 с,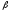 =75°.
Определить
=75°.
Определить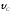 иb.
иb.
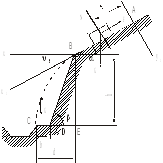
Решение:
рассмотрим движение камня на участке
АВ. Принимая
камень за материальную точку, покажем
действующие на него силы: вес
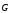 ,
нормальную реакцию
,
нормальную реакцию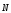 и силу трения скольжения
и силу трения скольжения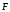 .
Составим
дифференциальное уравнение
движения камня на участке АВ:
.
Составим
дифференциальное уравнение
движения камня на участке АВ:
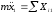
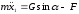
Сила трения
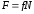 где
где
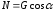
Таким образом
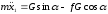
или
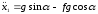
интегрируя дифференциальное уравнение дважды получаем:
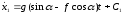

Для определения
постоянных интегрирования воспользуемся
начальными условиями задачи: при t
= 0, x01=0
и

Составим уравнения, полученные при интегрировании, для t=0:
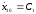
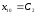
Найдем постоянные С1 = 0, С2 = 0
тогда
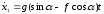
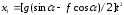
Для момента
 ,
когда камень покидает участок,
,
когда камень покидает участок,
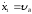
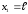
т.е
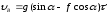
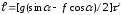
откуда
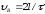
т.е.
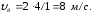
Рассмотрим движение камня от точки В до точки С.
Показав силу
тяжести
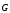 ,
действующую на камень, составим
дифференциальные уравнения его движения:
,
действующую на камень, составим
дифференциальные уравнения его движения:
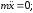
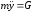
Начальные условия задачи; при t = 0
x0=0, y0 = 0
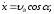
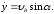
Интегрируем дифференциальные уравнения
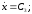
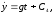
x = C3t + C5, y = gt2/2 + C4t + C5.
Напишем полученные уравнения для t = 0
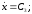
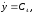
x=C5; y = C6.
Отсюда найдем, что
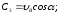
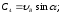
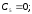
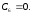
Получим следующие уравнения проекций скоростей камня:
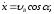
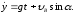
И уравнения его движения:
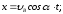
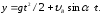
Уравнение траектории камня найдем, исключив параметр t из уравнений движения. Определив t из первого уравнения и подставив его значение во второе, получаем уравнение параболы:
В момент падения y = h, x = d.
Определяя d из уравнения траектории, найдем
d1 = 2,11 м, d2 = –7,75 м.
Так как траекторией движения камня является ветвь параболы с положительными абсциссами ее точек, то d = 2,11 м.
Минимальная ширина полки
b = d – ED = d – h/tg75°, или b = 0,77 м.
Используя уравнение
движения камня
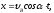 найдем время Т движения камня от точки
В до точки С: Т = 0,53 с.
найдем время Т движения камня от точки
В до точки С: Т = 0,53 с.
Скорость камня при падении найдем через проекции скорости на оси координат
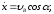
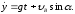
По формуле
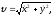
Для момента падения t = T = 0,53с
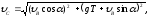
или