- •Кафедра инженерной графики и механики
- •Введение
- •1. Порядок выбора вариантов и оформления расчетно-графических работ
- •2. Задача 1. «Сложное движение точки»
- •3. Задача 2. « Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил»
- •4. Задача 3. «Применение теоремы об изменении кинетического момента к определению угловой скорости твердого тела»
- •5. Задача 4. «Применение теоремы об изменении кинетической энергии к изучению движения механической системы»
2. Задача 1. «Сложное движение точки»
Прямоугольная пластина (рис. 0 – 5) или круглая пластина радиуса R= 60см (рис. 6 – 9) вращается вокруг неподвижной оси с постоянной угловой скоростью ω, заданной в таблице (при знаке минуc направление вращения противоположно направлению показанному на рисунке). Ось вращения на рис. 0, 1, 2, 3, 6, 7 перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. 4, 5, 8, 9 ось вращения О1О2 -вертикальная (лежит в плоскости пластины).
По пластине, вдоль прямой BD (рис. 0 – 5) или по окружности радиуса R (т.е. по ободу пластины) (рис. 6 – 9), движется точка М. Закон её относительного движения, выражаемый уравнением S=AM=f (t) (S в сантиметрах, t в секундах), задан в таблице; там же даны размеры а и h (для рис. с 0 по 5 - в столбцах 3 и 4; для рис. с 6 по 9 – в столбцах 5 и 6). Положительное направление отсчёта координаты S =AM от точки А к точке D (на всех рисунках точка M показана в положении, при котором S=AM положительно).
Определить абсолютную скорость и абсолютное ускорение точки М в момент времени t = 1с.
|
№ условия |
ω рад/с |
|
Puc. 0 – 5 |
Puc. 6 – 9 | |
|
a, см |
S=AM=f (t) |
h |
| ||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
0 |
– 2 |
16 |
60(t4 – 2t2) + 56 |
R |
|
|
1 |
4 |
20 |
60(t3 – 2t2) |
R |
|
|
2 |
3 |
8 |
80(2t2 – t3) – 48 |
R |
|
|
3 |
– 4 |
12 |
40(t2 – 3t) + 32 |
|
|
|
4 |
3 |
10 |
50(t3 – t) – 30 |
R |
|
|
5 |
2 |
12 |
50(3t – t2) – 64 |
R |
|
|
6 |
4 |
20 |
40(t – 2t3) – 40 |
|
|
|
7 |
– 5 |
10 |
80(t2 – t) + 40 |
R |
|
|
8 |
2 |
8 |
60(t – t3) + 24 |
R |
|
|
9 |
– 5 |
16 |
40(3t2 – t4) – 32 |
|
|
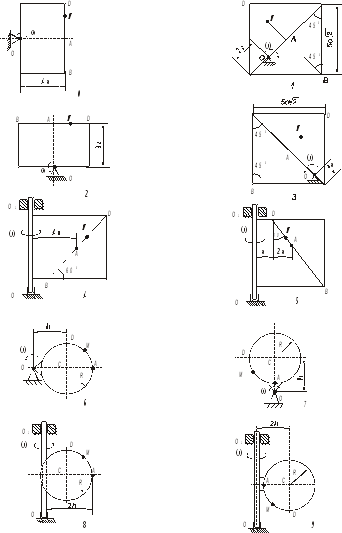

Пример решения Задачи 1
Условие задачи:
Прямоугольная
пластина вращается вокруг неподвижной
оси перпендикулярной плоскости чертежа
и проходящей через точку О с постоянной
угловой скоростью
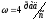 ,
,
По поверхности
пластины, по прямой BD,
движется точка M.
Закон её движения задаётся функцией
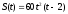 .
Начало отсчёта координатыS
– точка А, положительное направление
отсчета координаты
.
Начало отсчёта координатыS
– точка А, положительное направление
отсчета координаты
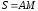 -
от точкиA
к точке D.
-
от точкиA
к точке D.
Требуется найти абсолютную скорость и абсолютное ускорение точки M в момент времени t = 1 с
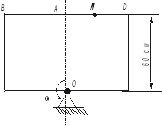
Рис. 1.1
Решение задачи
Движение точки M- сложное. Её абсолютное движение складывается из движения по стороне ВД пластины – относительное движение и движения точки М вместе с вращающейся пластиной – переносное движение.
Абсолютная скорость точки М
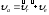 ,
,
где
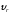 – относительная скорость
– относительная скорость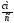 ;
;
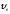 –переносная
скорость
–переносная
скорость
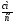 ;
;
Абсолютное ускорение точки
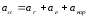
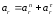
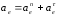 ,
,
где
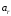 –
относительное ускорение;
–
относительное ускорение;
 – переносное
ускорение,
– переносное
ускорение,
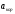 – ускорение
Кориолиса,
– ускорение
Кориолиса,
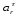 –-
относительное касательное ускорение,
–-
относительное касательное ускорение,
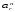 – относительное
нормальное ускорение.
– относительное
нормальное ускорение.
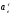 – переносное
касательное ускорение,
– переносное
касательное ускорение,
 – переносное
нормальное ускорение.
– переносное
нормальное ускорение.
Рассмотрим относительное движение точки.
Скорость относительного движения
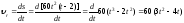
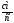
Относительное касательное ускорение

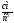
Относительное нормальное ускорение
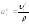
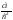 ,
так как точка M
в относительном
движении перемещается по
прямой BD,
то
,
так как точка M
в относительном
движении перемещается по
прямой BD,
то
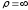 ,
тогда
,
тогда
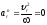
Модуль
относительного ускорения
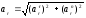
Для момента времени t=1 c :
AM=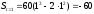
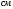 (знак минус показывает, что движение
направлено от точки А к точке В);
(знак минус показывает, что движение
направлено от точки А к точке В);
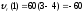
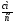
(вектор
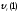 направлен кB);
направлен кB);
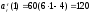
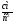 ( вектор
направлен
к точке D);
( вектор
направлен
к точке D);
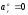
 (
(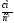 )
)
Строим чертеж с нанесением положения точки, векторов относительных скорости и ускорения в момент t = 1 c
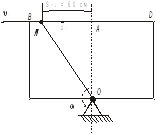
Рис.1.2
Переносное движение
Угловая
скорость переносного движения
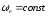 ,
следовательно, угловое переносное
ускорение
,
следовательно, угловое переносное
ускорение
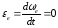
Переносная скорость точки M
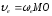
В момент времени t=1c
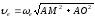
Переносное касательное ускорение
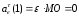
Переносное нормальное ускорение
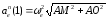
Кориолисово ускорение
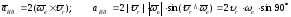
(вектор
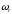 направлен вдоль оси вращения)
направлен вдоль оси вращения)
Вектор
 перпендикулярен плоскости, в которой
расположены векторы
перпендикулярен плоскости, в которой
расположены векторы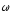 и
и
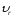 и направлен в ту сторону, чтобы с его
конца поворот вектора
и направлен в ту сторону, чтобы с его
конца поворот вектора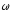 (первый сомножитель) до совмещения его
с вектором
(первый сомножитель) до совмещения его
с вектором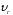 (второй
сомножитель)
по кратчайшему пути был виден происходящим
против хода стрелки часов.
(второй
сомножитель)
по кратчайшему пути был виден происходящим
против хода стрелки часов.
Абсолютное движение
Абсолютная скорость точки М
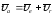
Сумму векторов найдем через проекции на оси координат X и У
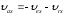
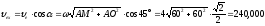 (
( )
)
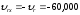
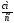
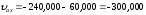
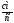


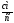
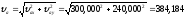
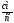
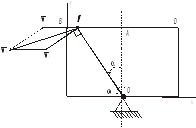
Рис.1.3
Абсолютное ускорение
Абсолютное ускорение точки М для нашего случая
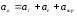
Сумму векторов найдем через их проекции на оси координат X и У
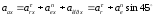
для момента времени t=1c
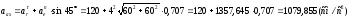
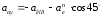
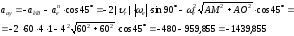
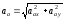 (см/с2)
(см/с2)
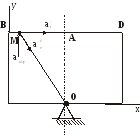
Рис.1.4

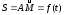
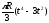
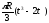
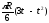
 R
R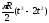

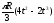
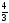 R
R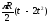
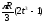
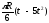
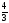 R
R