
- •Рязань 2009
- •Глава 1. Предел функции
- •1.1. Определение предела
- •1.2. Операции над пределами
- •1.3. Замечательные пределы
- •1.4. Примеры
- •1.5. Варианты заданий
- •1.6. Контрольные вопросы Глава 2. Производная и дифференциал
- •2.1 Понятие производной
- •2.2. Геометрический и физический смысл производной
- •2.3. Таблица производных
- •2.4. Основные правила дифференцирования
- •2.5. Производные высших порядков
- •2.6. Дифференциал функции
- •2.7. Геометрический смысл и свойства дифференциала
- •2.8. Дифференциалы высших порядков
- •2.9. Примеры
- •2.10. Варианты заданий
- •2.11. Контрольные вопросы
- •Глава 3. Исследование функций и построение графиков
- •3.1. Промежутки монотонности и знакопостоянства
- •3.2. Экстремумы функции
- •3.3. Выпуклость и вогнутость функции. Точка перегиба
- •3.4. Асимптоты
- •3.5.Общая схема исследования функции и построение графиков
- •3.6. Примеры
- •3.7. Варианты заданий
- •3.8. Контрольные вопросы
- •Глава 4. Функции нескольких переменных
- •4.1. Определение функции нескольких переменных
- •4.2. Частные производные
- •4.3. Полный дифференциал
- •4.5. Примеры
- •4.6. Варианты заданий
- •4.7. Контрольные вопросы Глава 5. Численное дифференцирование
- •5.1. Формулы для вычисления первой производной
- •5.2. Формулы второй производной
- •5.3. Примеры
- •5.4. Варианты заданий
- •5.5. Контрольные вопросы Глава 6 Основы интерполяции.
- •6.1. Постановка задачи
- •Интерполяционные формулы конечных разностей
- •6.3. Интерполяционные формулы центральных разностей
- •6.4. Интерполирование функции с не равноотстоящими узлами
- •6.5. Варианты заданий
- •6.6. Контрольные вопросы Глава 7. Неопределенный интеграл
- •7.1. Первообразная функция и неопределенный интеграл
- •7.2. Основные свойства неопределенного интеграла
- •7.3. Таблица простейших интегралов
- •7.4. Основные методы интегрирования
- •7.4.1. Непосредственное интегрирование
- •7.4.2. Метод подстановки (замена переменной)
- •7.4.3. Интегрирование по частям
- •7.5. Примеры
- •7.6. Варианты заданий
- •7.7. Контрольные вопросы
- •Глава 8. Определенный интеграл
- •8.1. Основные понятия и свойства определенного интеграла
- •Свойства определенного интеграла
- •8.2. Основные методы интегрирования
- •8.2.1. Формула Ньютона-Лейбница
- •8.2.2. Метод подстановки
- •8.2.3. Интегрирование по частям
- •8.3. Примеры
- •8.4. Варианты заданий
- •8.5. Биологические, физические и медицинские приложения определенного интеграла
- •8.5.1. Примеры задач прикладного характера.
- •8.5.2. Примеры решения задач.
- •8.5.3. Варианты заданий
- •Глава 9. Численное интегрирование
- •9.1. Формула прямоугольников
- •9.2. Формула трапеций
- •9.3. Метод средних
- •9.4. Формула Симпсона
- •9.5. Примеры
- •9.6. Варианты заданий
- •9.7. Контрольные вопросы
- •Глава 10. Дифференциальные уравнения
- •10.1. Основные определения
- •10.2. Уравнения с разделяющимися переменными
- •10.3. Однородные уравнения первого порядка
- •10.4. Линейные уравнения первого порядка
- •9.5. Примеры
- •I. Метод Лагранжа
- •II. Метод Бернулли
- •1) Метод вариации произвольной постоянной
- •2) Метод подстановки
- •10.6. Варианты заданий
- •10.7. Применение дифференциальных уравнений в биологии и медицине.
- •10.8. Варианты заданий
- •10.9. Контрольные вопросы
- •Глава 11. Численные методы решения дифференциальных уравнений
- •11.1. Метод Эйлера
- •10.2. Метод Рунге – Кутта
- •10.3. Примеры
- •11.4. Варианты заданий
- •11.4. Контрольные вопросы
- •Глава 12. Элементы теории вероятностей
- •12.1. Случайное событие
- •12.2. Комбинаторика
- •12.3. Вероятность случайного события
- •Закон сложения вероятностей
- •12.5. Варианты заданий
- •12.6. Условная вероятность, закон умножения вероятностей
- •12.7. Варианты заданий
- •12.8. Формулы полной вероятности и Байеса
- •12.9. Варианты заданий
- •11.10. Формулы Бернулли, Пуассона и Муавра-Лапласа
- •12.11. Варианты заданий
- •12.2. Случайные величины
- •12.2.1. Закон распределения случайной величины
- •12.2.2. Функция распределения случайных величин
- •12.2.3. Числовые характеристики дискретной случайной величины
- •12.2.4. Плотность вероятности непрерывных случайных величин
- •12.2.5. Нормальный закон распределения
- •12.3. Варианты заданий
- •Глава 13. Статистический анализ результатов исследований
- •13.1. Основные понятия математической статистики
- •13.1. Варианты заданий
- •13.2. Статистические оценки параметров распределения. Выборочные характеристики
- •13.2.1. Характеристики положения
- •13.2.2. Характеристики рассеяния вариант вокруг своего среднего
- •13.3. Варианты заданий
- •13.4. Оценка параметров генеральной совокупности по ее выборке
- •13.4.1. Точечная оценка параметров генеральной совокупности
- •13.5. Варианты заданий
- •13.6. Интервальная оценка параметров генеральной совокупности
- •13.7. Варианты заданий
- •1.8. Контрольные вопросы
- •Глава 14. Корреляционный и регрессионный анализ
- •14.1. Функциональная и корреляционная зависимости
- •14.2. Коэффициент линейной корреляции и его свойства
- •14.3. Проверка гипотезы о значимости выборочного коэффициента линейной корреляции
- •14.4. Выборочное уравнение линейной регрессии. Метод наименьших квадратов
- •14.5. Нелинейная регрессия
- •14.6. Варианты заданий
- •Приложение
- •Критические значения выборочного коэффициента корреляции
- •Критерий Колмогорова – Смирнова Точные и асимптотические границы для верхней грани модуля разности истинной и эмпирической функции распределения
- •Распределение Пирсона (х2– распределение)
- •Распределение Фишера – Снедекора (f-распределение)
- •Библиографический список
- •Содержание
- •Глава 13. Статистический анализ результатов исследований 160
- •Глава 14. Корреляционный и регрессионный анализ 180
Приложение
t-распределение (распределение Стьюдента)
P (t > t) = и P (t > t) =
Таблица 1
|
k |
Односторонняя критическая область () | |||||||
|
0,1 |
0,05 |
0,025 |
0,01 |
0,005 |
0,0025 |
0,001 |
0,0005 | |
|
Двусторонняя критическая область () | ||||||||
|
0,2 |
0,1 |
0,05 |
0,02 |
0,01 |
0,005 |
0,002 |
0,001 | |
|
1 2 3 4 5
6 7 8 9 10
11 12 13 14 15
16 17 18 19 20
21 22 23 24 25
26 27 28 29 30
40 60 120 |
3,08 1,89 1,64 1,53 1,48
1,44 1,41 1,40 1,38 1,37
1,36 1,36 1,35 1,34 1,34
1,34 1,33 1,33 1,33 1,33
1,32 1,32 1,32 1,32 1,32
1,32 1,31 1,31 1,31 1,31
1,30 1,30 1,29 1,28 |
6,31 2,92 2,35 2,13 2,02
1,94 1,89 1,86 1,83 1,81
1,80 1,78 1,77 1,76 1,75
1,75 1,74 1,73 1,73 1,72
1,72 1,72 1,71 1,71 1,71
1,71 1,70 1,70 1,70 1,70
1,68 1,67 1,66 1,64 |
12,71 4,30 3,18 2,78 2,57
2,45 2,36 2,31 2,26 2,23
2,20 2,18 2,16 2,14 2,13
2,12 2,11 2,10 2,09 2,09
2,8 2,07 2,07 2,06 2,06
2,06 2,05 2,05 2,05 2,04
2,02 2,00 1,98 1,96 |
31,82 6,96 4,54 3,75 3,36
3,14 3,00 2,90 2,82 2,76
2,72 2,68 2,65 2,62 2,60
2,58 2,57 2,55 2,54 2,53
2,52 2,51 2,50 2,49 2,49
2,48 2,47 2,47 2,46 2,46
2,42 2,39 2,36 2,33 |
63,66 9,92 5,84 4,60 4,03
3,71 3,50 3,36 3,25 3,17
3,11 3,05 3,01 2,98 2,95
2,92 2,90 2,88 2,86 2,85
2,83 2,82 2,81 2,80 2,79
2,78 2,77 2,76 2,76 2,75
2,70 2,66 2,62 2,58 |
127,32 14,09 7,45 5,60 4,77
4,32 4,03 3,83 3,69 3,58
3,50 3,43 3,37 3,33 3,29
3,25 3,22 3,20 3,17 3,15
3,14 3,12 3,10 3,09 3,08
3,07 3,06 3,05 3,04 3,03
2,97 2,91 2,85 2,81 |
318,30 22,33 10,21 7,17 5,89
5,21 4,79 4,50 4,30 4,14
4,02 3,93 3,85 3,79 3,73
3,69 3,65 3,61 3,58 3,55
3,53 3,51 3,48 3,47 3,45
3,44 3,42 3,41 3,40 3,39
3,31 3,23 3,16 3,09 |
636,61 31,60 12,92 8,61 6,87
5,96 5,41 5,04 4,78 4,59
4,44 4,32 4,22 4,14 4,07
4,02 3,97 3,92 3,88 3,85
3,82 3,79 3,77 3,75 3,73
3,71 3,69 3,67 3,66 3,65
3,55 3,46 3,37 3,29 |
Таблица значений функции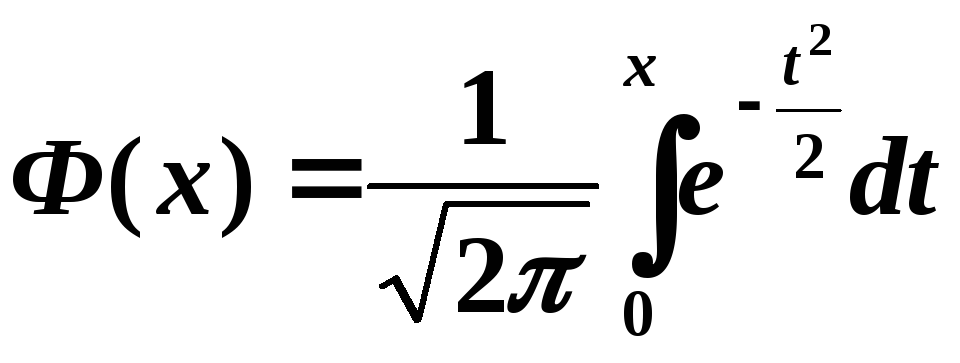
Таблица 2
|
x |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0,0 |
0,00000 |
00399 |
00798 |
01197 |
01595 |
01994 |
02392 |
02790 |
03188 |
03586 |
|
0,1 |
03983 |
04380 |
04776 |
05172 |
05567 |
05962 |
06356 |
06749 |
07142 |
07535 |
|
0,2 |
07926 |
08317 |
08706 |
09095 |
09483 |
09871 |
10257 |
10642 |
11026 |
11409 |
|
0,3 |
11791 |
12172 |
12552 |
12930 |
13307 |
13683 |
14058 |
14431 |
14803 |
15173 |
|
0,4 |
15542 |
15910 |
16276 |
16640 |
17003 |
17364 |
17724 |
18082 |
18439 |
18793 |
|
0,5 |
19146 |
19497 |
19847 |
20194 |
20540 |
20884 |
21226 |
21566 |
21904 |
22240 |
|
0,6 |
22575 |
22907 |
23237 |
23565 |
23891 |
24215 |
24537 |
24857 |
25175 |
25490 |
|
0,7 |
25804 |
26115 |
26424 |
26730 |
27035 |
27337 |
27637 |
27935 |
28230 |
28524 |
|
0,8 |
28814 |
29103 |
29389 |
29673 |
29955 |
30234 |
30511 |
30785 |
31057 |
31327 |
|
0,9 |
31594 |
31859 |
32121 |
32381 |
32639 |
32894 |
33147 |
33398 |
33646 |
33891 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1,0 |
34134 |
34375 |
34614 |
34850 |
35083 |
35314 |
35543 |
35769 |
35993 |
36214 |
|
1,1 |
36433 |
36650 |
36864 |
37076 |
37286 |
37493 |
37698 |
37900 |
38100 |
38298 |
|
1,2 |
38493 |
38686 |
38877 |
39065 |
39251 |
39435 |
39617 |
39796 |
39973 |
40147 |
|
1,3 |
40320 |
40490 |
40658 |
40824 |
40988 |
41149 |
41309 |
41466 |
41621 |
41774 |
|
1,4 |
41924 |
42073 |
42220 |
42364 |
42507 |
42647 |
42786 |
42922 |
43056 |
43189 |
|
1,5 |
43319 |
43448 |
43574 |
43699 |
43822 |
43943 |
44062 |
44179 |
44295 |
44408 |
|
1,6 |
44520 |
44630 |
44738 |
44845 |
44950 |
45053 |
45154 |
45254 |
45352 |
45449 |
|
1,7 |
45543 |
45637 |
45728 |
45818 |
45907 |
45994 |
46080 |
46164 |
46246 |
46327 |
|
1,8 |
46407 |
46485 |
46582 |
46638 |
46712 |
46784 |
46856 |
46926 |
46995 |
47062 |
|
1,9 |
47128 |
47193 |
47257 |
47320 |
47381 |
47441 |
47500 |
47558 |
47615 |
47670 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2,0 |
47725 |
47778 |
47831 |
47882 |
47932 |
47982 |
48030 |
48077 |
48124 |
48169 |
|
2,1 |
48214 |
48257 |
48300 |
48341 |
48382 |
48422 |
48461 |
48500 |
48537 |
48574 |
|
2,2 |
48610 |
48645 |
48679 |
48713 |
48745 |
48778 |
48809 |
48840 |
48870 |
48899 |
|
2,3 |
48928 |
48956 |
48983 |
49010 |
49036 |
49061 |
49086 |
49111 |
49134 |
49158 |
|
2,4 |
49180 |
49202 |
49224 |
49245 |
49266 |
49286 |
49305 |
49324 |
49343 |
49361 |
|
2,5 |
49379 |
49396 |
49413 |
49430 |
49446 |
49461 |
49477 |
49492 |
49506 |
49520 |
|
2,6 |
49534 |
49547 |
49560 |
49573 |
49585 |
49598 |
49609 |
49621 |
49632 |
49643 |
|
2,7 |
49653 |
49664 |
49674 |
49683 |
49693 |
49702 |
49711 |
49720 |
49728 |
49736 |
|
2,8 |
49744 |
49752 |
49760 |
49767 |
49774 |
49781 |
49788 |
49795 |
49801 |
49807 |
|
2,9 |
49813 |
49819 |
49825 |
49831 |
49836 |
49841 |
49846 |
49851 |
49856 |
49861 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3,0 |
0,49865 |
0,49865 |
3,1 |
49903 |
3,2 |
49931 |
3,3 |
49952 |
3,4 |
49986 |
|
3,5 |
49977 |
49977 |
3,6 |
49984 |
3,7 |
49989 |
3,8 |
49993 |
3,9 |
49995 |
|
4,0 |
499968 |
499968 |
- |
- |
- |
- |
- |
- |
- |
- |
