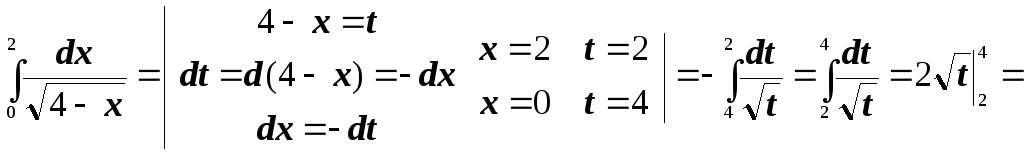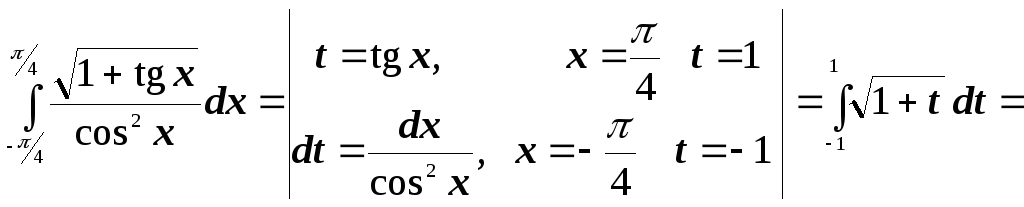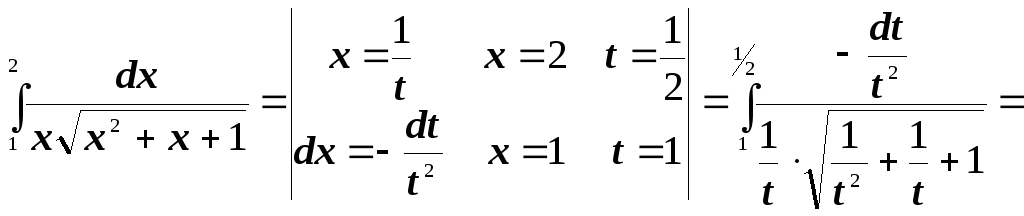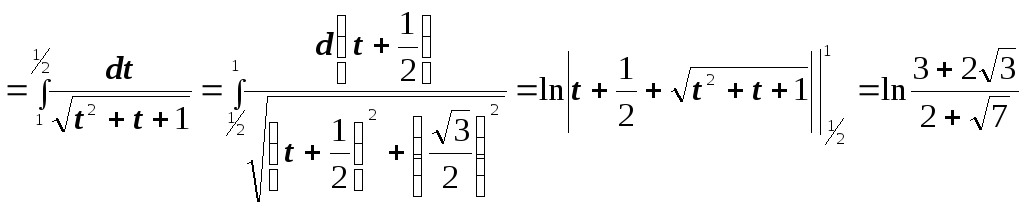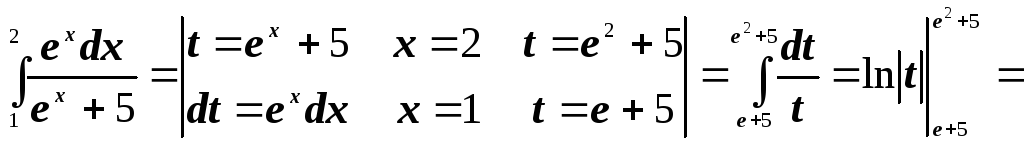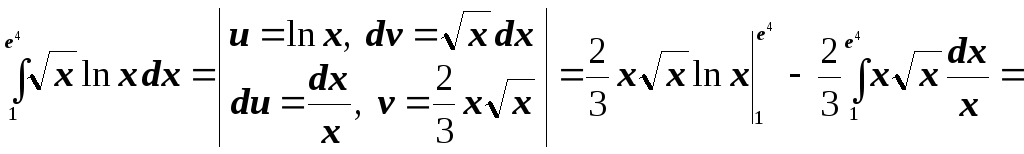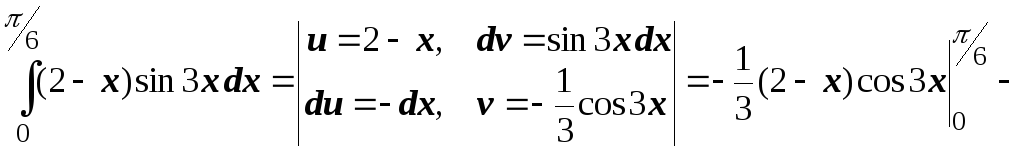- •Рязань 2009
- •Глава 1. Предел функции
- •1.1. Определение предела
- •1.2. Операции над пределами
- •1.3. Замечательные пределы
- •1.4. Примеры
- •1.5. Варианты заданий
- •1.6. Контрольные вопросы Глава 2. Производная и дифференциал
- •2.1 Понятие производной
- •2.2. Геометрический и физический смысл производной
- •2.3. Таблица производных
- •2.4. Основные правила дифференцирования
- •2.5. Производные высших порядков
- •2.6. Дифференциал функции
- •2.7. Геометрический смысл и свойства дифференциала
- •2.8. Дифференциалы высших порядков
- •2.9. Примеры
- •2.10. Варианты заданий
- •2.11. Контрольные вопросы
- •Глава 3. Исследование функций и построение графиков
- •3.1. Промежутки монотонности и знакопостоянства
- •3.2. Экстремумы функции
- •3.3. Выпуклость и вогнутость функции. Точка перегиба
- •3.4. Асимптоты
- •3.5.Общая схема исследования функции и построение графиков
- •3.6. Примеры
- •3.7. Варианты заданий
- •3.8. Контрольные вопросы
- •Глава 4. Функции нескольких переменных
- •4.1. Определение функции нескольких переменных
- •4.2. Частные производные
- •4.3. Полный дифференциал
- •4.5. Примеры
- •4.6. Варианты заданий
- •4.7. Контрольные вопросы Глава 5. Численное дифференцирование
- •5.1. Формулы для вычисления первой производной
- •5.2. Формулы второй производной
- •5.3. Примеры
- •5.4. Варианты заданий
- •5.5. Контрольные вопросы Глава 6 Основы интерполяции.
- •6.1. Постановка задачи
- •Интерполяционные формулы конечных разностей
- •6.3. Интерполяционные формулы центральных разностей
- •6.4. Интерполирование функции с не равноотстоящими узлами
- •6.5. Варианты заданий
- •6.6. Контрольные вопросы Глава 7. Неопределенный интеграл
- •7.1. Первообразная функция и неопределенный интеграл
- •7.2. Основные свойства неопределенного интеграла
- •7.3. Таблица простейших интегралов
- •7.4. Основные методы интегрирования
- •7.4.1. Непосредственное интегрирование
- •7.4.2. Метод подстановки (замена переменной)
- •7.4.3. Интегрирование по частям
- •7.5. Примеры
- •7.6. Варианты заданий
- •7.7. Контрольные вопросы
- •Глава 8. Определенный интеграл
- •8.1. Основные понятия и свойства определенного интеграла
- •Свойства определенного интеграла
- •8.2. Основные методы интегрирования
- •8.2.1. Формула Ньютона-Лейбница
- •8.2.2. Метод подстановки
- •8.2.3. Интегрирование по частям
- •8.3. Примеры
- •8.4. Варианты заданий
- •8.5. Биологические, физические и медицинские приложения определенного интеграла
- •8.5.1. Примеры задач прикладного характера.
- •8.5.2. Примеры решения задач.
- •8.5.3. Варианты заданий
- •Глава 9. Численное интегрирование
- •9.1. Формула прямоугольников
- •9.2. Формула трапеций
- •9.3. Метод средних
- •9.4. Формула Симпсона
- •9.5. Примеры
- •9.6. Варианты заданий
- •9.7. Контрольные вопросы
- •Глава 10. Дифференциальные уравнения
- •10.1. Основные определения
- •10.2. Уравнения с разделяющимися переменными
- •10.3. Однородные уравнения первого порядка
- •10.4. Линейные уравнения первого порядка
- •9.5. Примеры
- •I. Метод Лагранжа
- •II. Метод Бернулли
- •1) Метод вариации произвольной постоянной
- •2) Метод подстановки
- •10.6. Варианты заданий
- •10.7. Применение дифференциальных уравнений в биологии и медицине.
- •10.8. Варианты заданий
- •10.9. Контрольные вопросы
- •Глава 11. Численные методы решения дифференциальных уравнений
- •11.1. Метод Эйлера
- •10.2. Метод Рунге – Кутта
- •10.3. Примеры
- •11.4. Варианты заданий
- •11.4. Контрольные вопросы
- •Глава 12. Элементы теории вероятностей
- •12.1. Случайное событие
- •12.2. Комбинаторика
- •12.3. Вероятность случайного события
- •Закон сложения вероятностей
- •12.5. Варианты заданий
- •12.6. Условная вероятность, закон умножения вероятностей
- •12.7. Варианты заданий
- •12.8. Формулы полной вероятности и Байеса
- •12.9. Варианты заданий
- •11.10. Формулы Бернулли, Пуассона и Муавра-Лапласа
- •12.11. Варианты заданий
- •12.2. Случайные величины
- •12.2.1. Закон распределения случайной величины
- •12.2.2. Функция распределения случайных величин
- •12.2.3. Числовые характеристики дискретной случайной величины
- •12.2.4. Плотность вероятности непрерывных случайных величин
- •12.2.5. Нормальный закон распределения
- •12.3. Варианты заданий
- •Глава 13. Статистический анализ результатов исследований
- •13.1. Основные понятия математической статистики
- •13.1. Варианты заданий
- •13.2. Статистические оценки параметров распределения. Выборочные характеристики
- •13.2.1. Характеристики положения
- •13.2.2. Характеристики рассеяния вариант вокруг своего среднего
- •13.3. Варианты заданий
- •13.4. Оценка параметров генеральной совокупности по ее выборке
- •13.4.1. Точечная оценка параметров генеральной совокупности
- •13.5. Варианты заданий
- •13.6. Интервальная оценка параметров генеральной совокупности
- •13.7. Варианты заданий
- •1.8. Контрольные вопросы
- •Глава 14. Корреляционный и регрессионный анализ
- •14.1. Функциональная и корреляционная зависимости
- •14.2. Коэффициент линейной корреляции и его свойства
- •14.3. Проверка гипотезы о значимости выборочного коэффициента линейной корреляции
- •14.4. Выборочное уравнение линейной регрессии. Метод наименьших квадратов
- •14.5. Нелинейная регрессия
- •14.6. Варианты заданий
- •Приложение
- •Критические значения выборочного коэффициента корреляции
- •Критерий Колмогорова – Смирнова Точные и асимптотические границы для верхней грани модуля разности истинной и эмпирической функции распределения
- •Распределение Пирсона (х2– распределение)
- •Распределение Фишера – Снедекора (f-распределение)
- •Библиографический список
- •Содержание
- •Глава 13. Статистический анализ результатов исследований 160
- •Глава 14. Корреляционный и регрессионный анализ 180
8.3. Примеры
№1. Используя формулу Ньютона-Лейбница, найти интегралы:
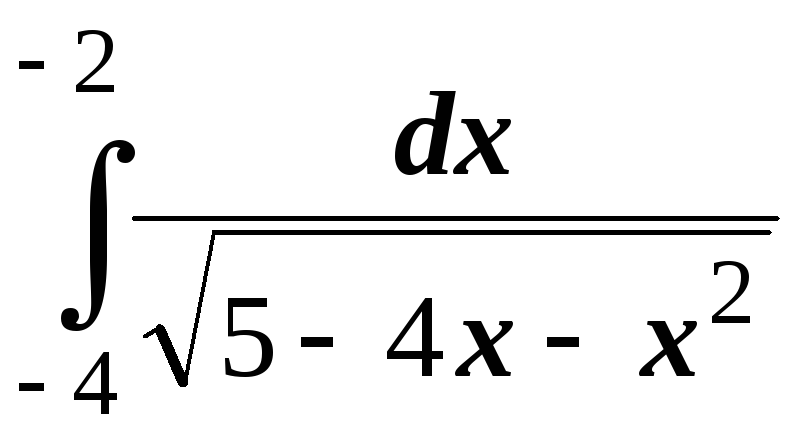 ;
; ;
;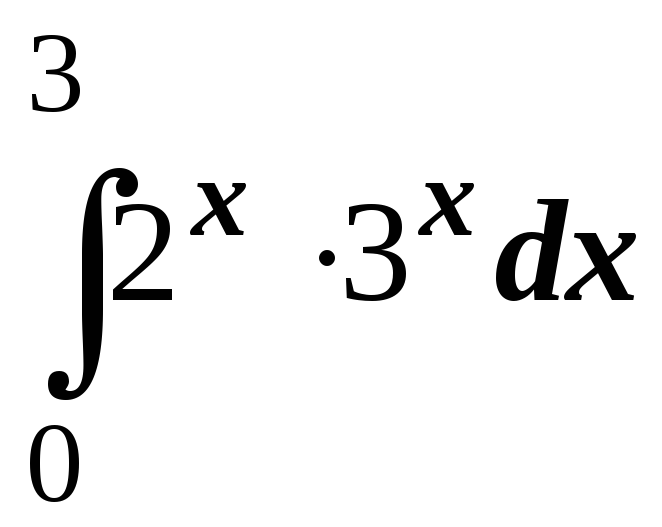 ;
;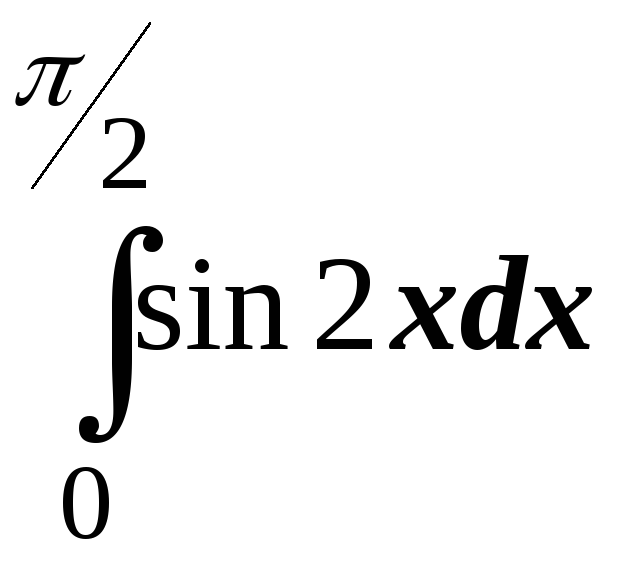 .
.
Решение.
Для нахождения первообразной проведем преобразования, чтобы получить табличный интеграл (в подкоренном выражении выделим полный квадрат):
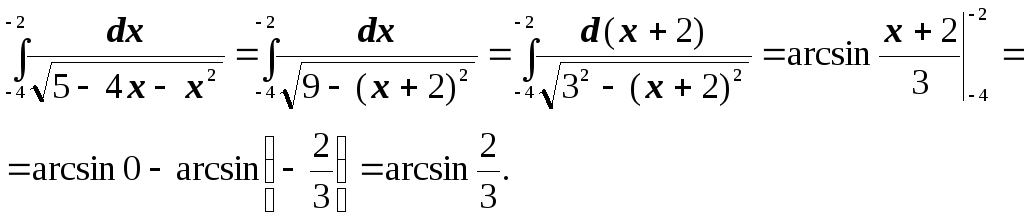
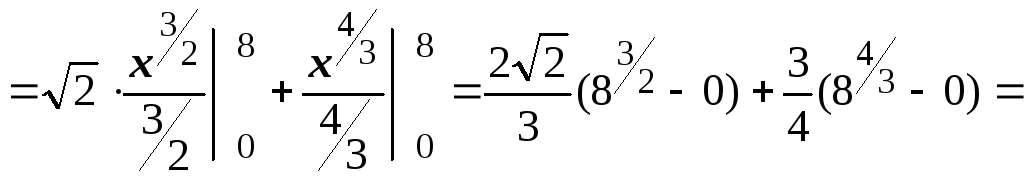
![]() .
.
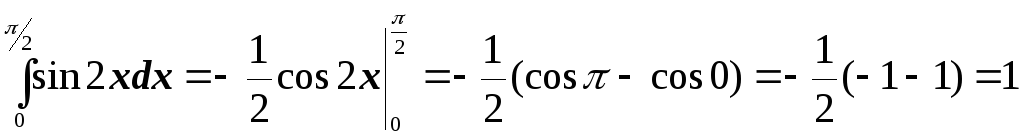 .
.
№2. Вычислить интегралы методом подстановки:
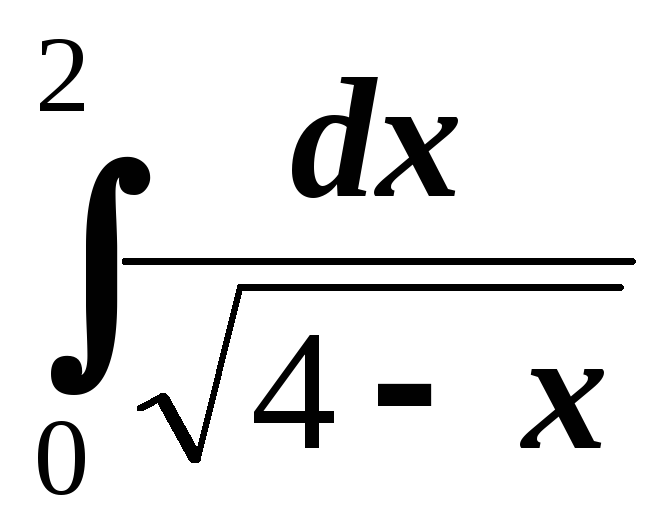 ;
;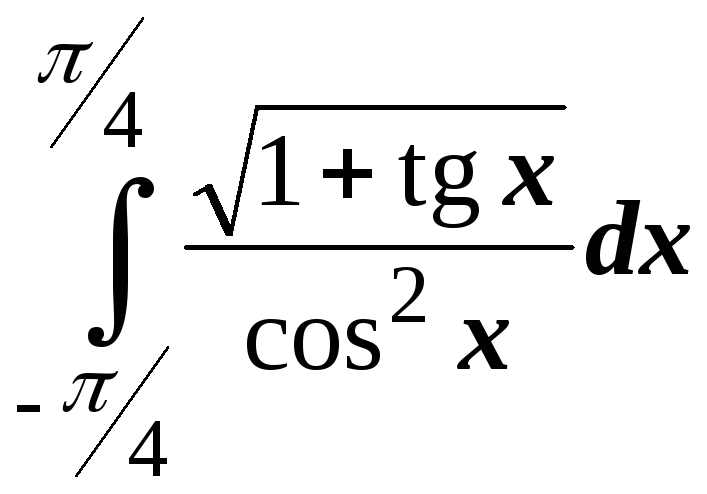 ;
;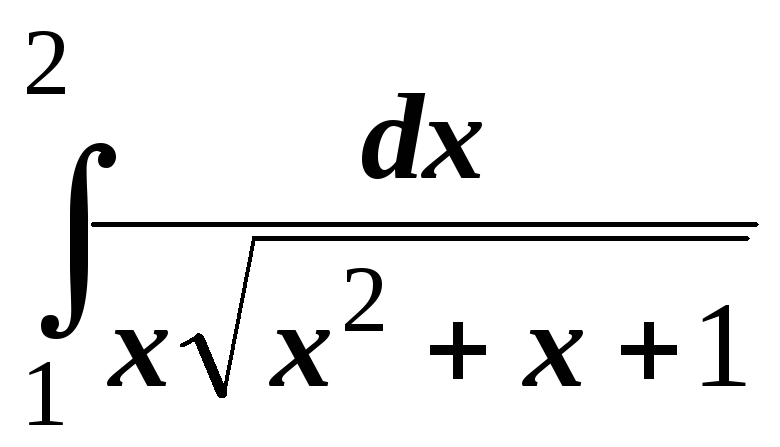 ;
;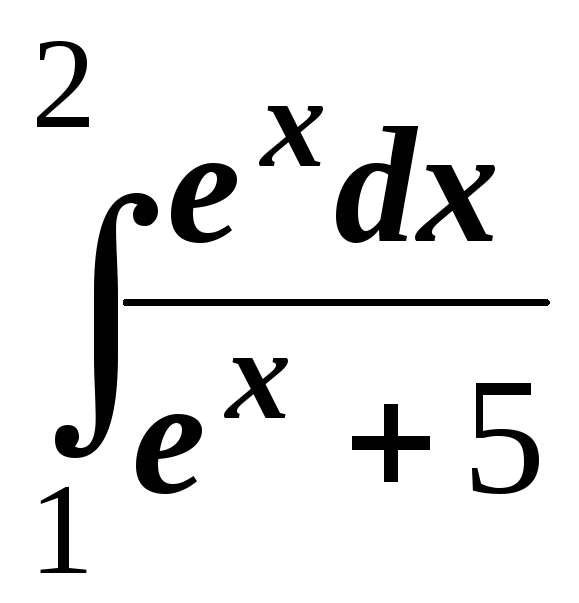 .
.
Решение.
![]()
![]() .
.
№3. Вычислить интегралы, применяя формулу интегрирования по частям:
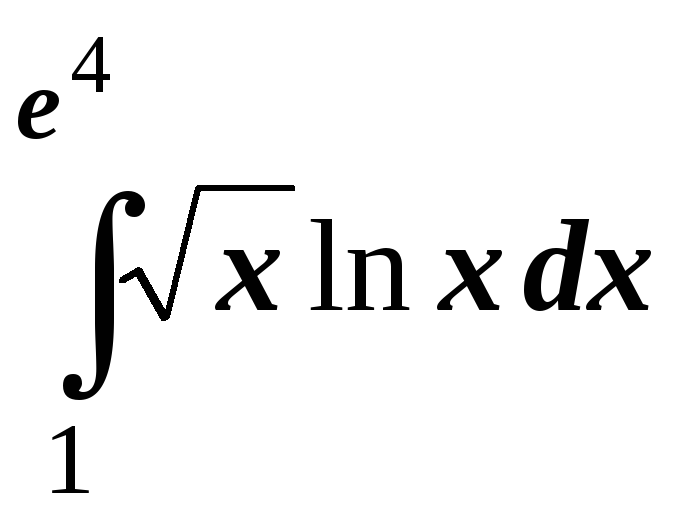 ;
;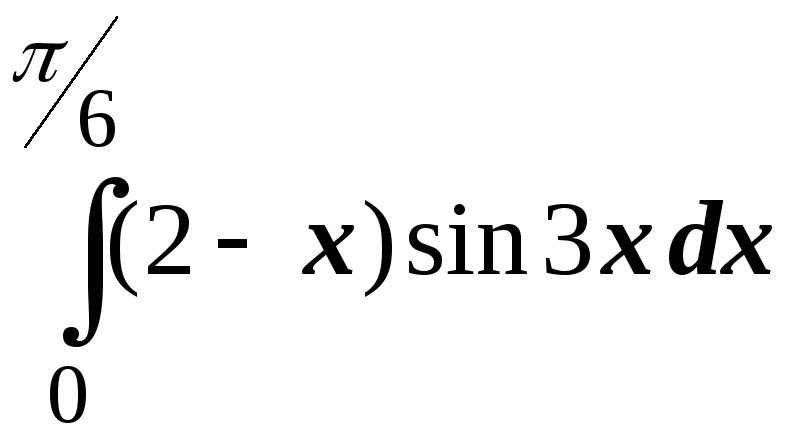 .
.
Решение.
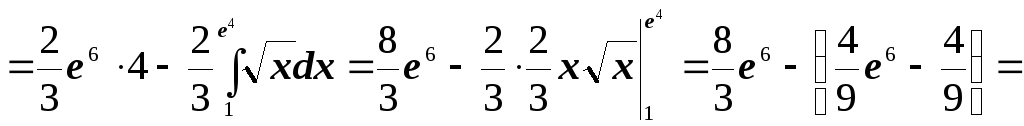
![]()
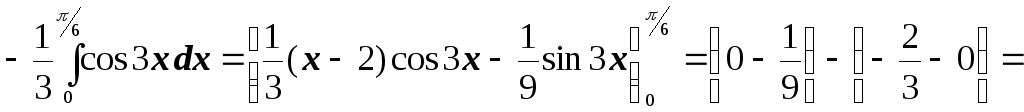
![]()
8.4. Варианты заданий
№8.1. Вычислить интегралы по формуле Ньютона-Лейбница:
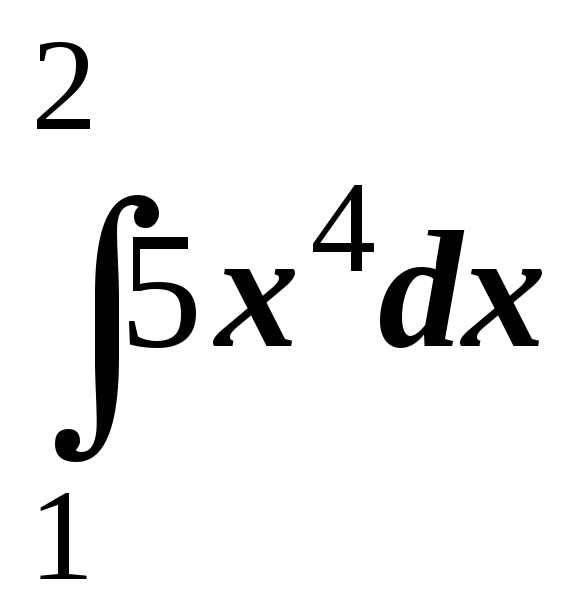 ;
;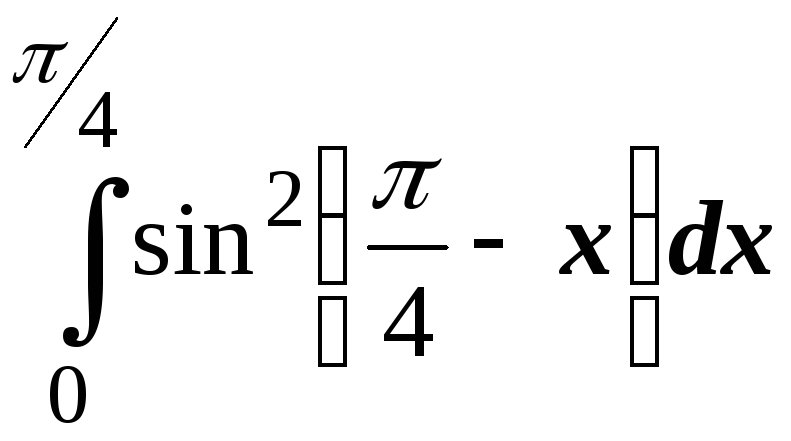 ;
;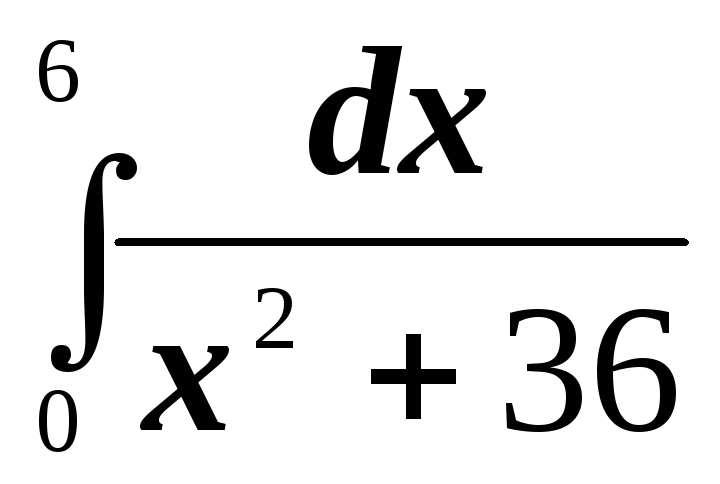 ;
;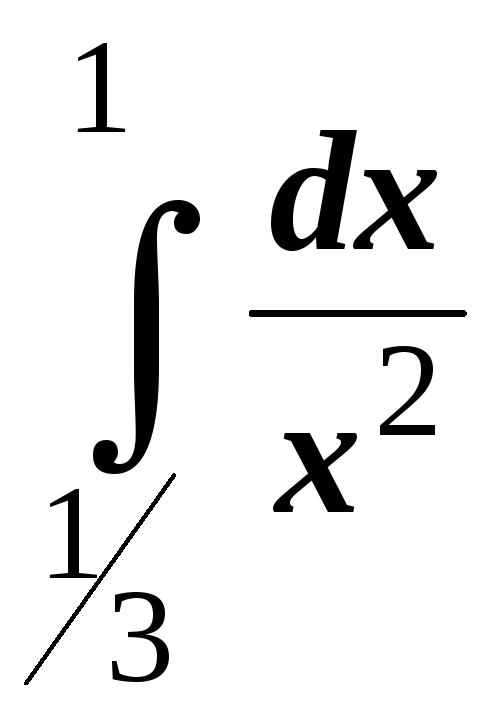 ;
;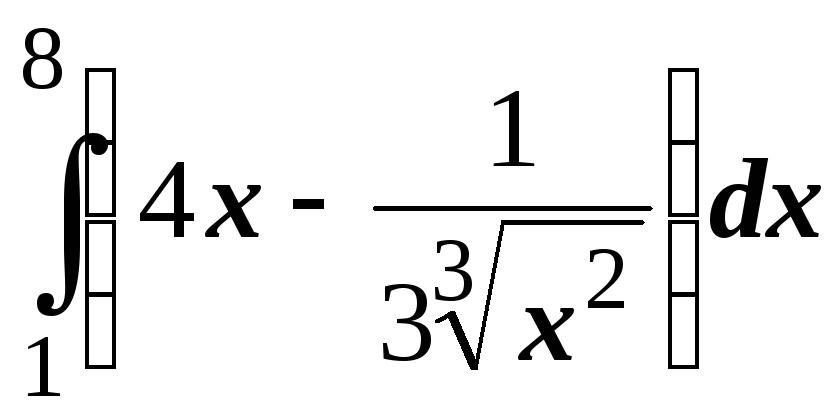 ;
;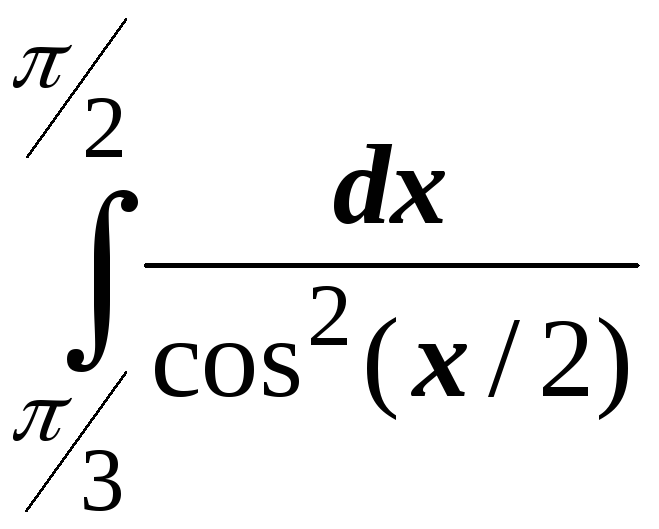 ;
;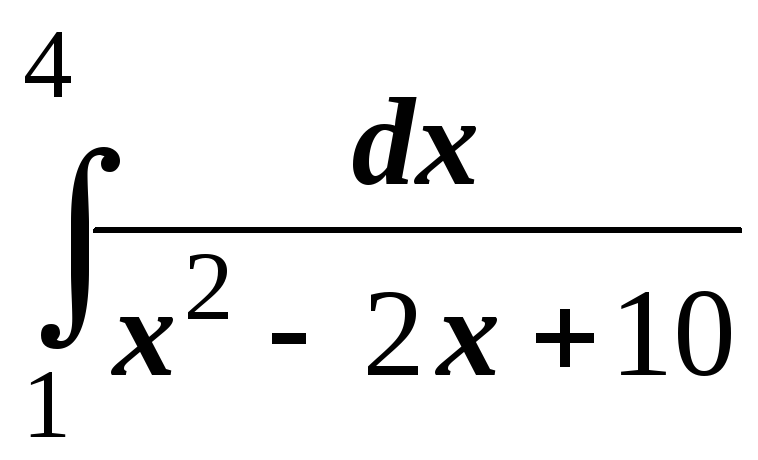 ;
;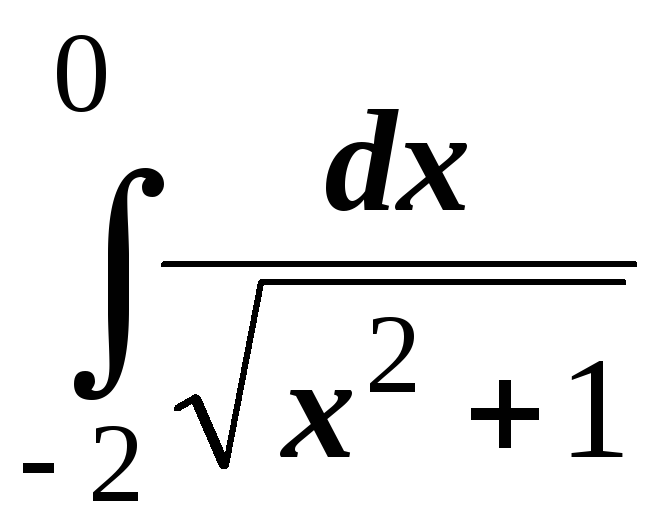 ;
;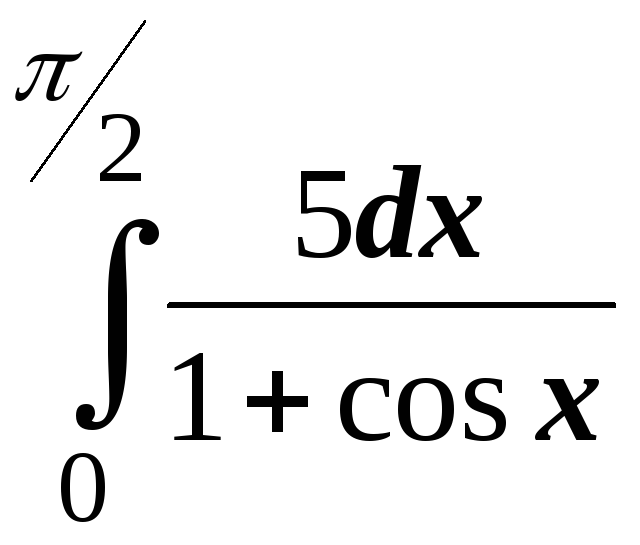 ;
;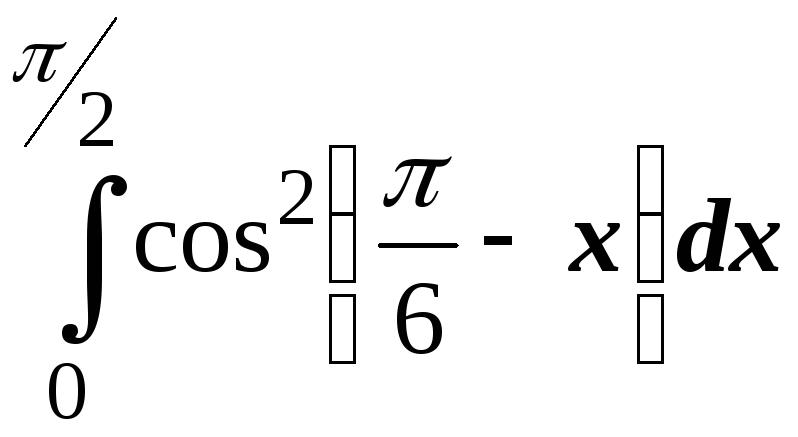 ;
;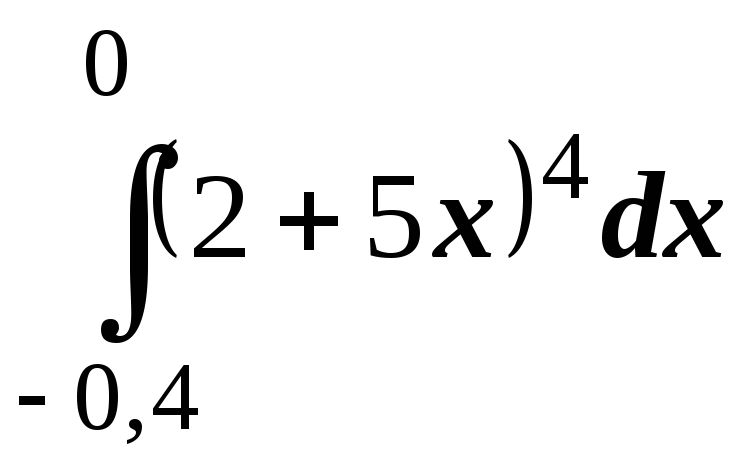 ;
;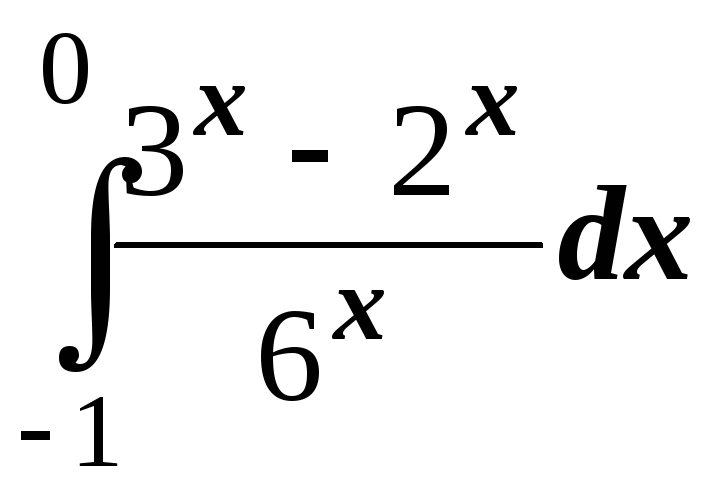 ;
;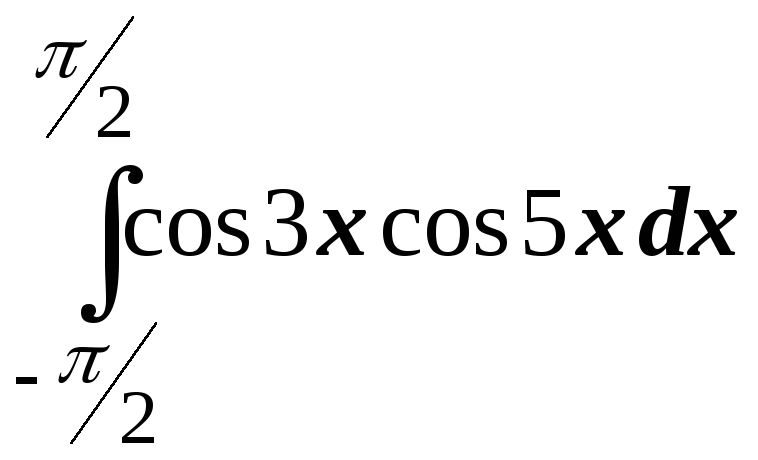 ;
;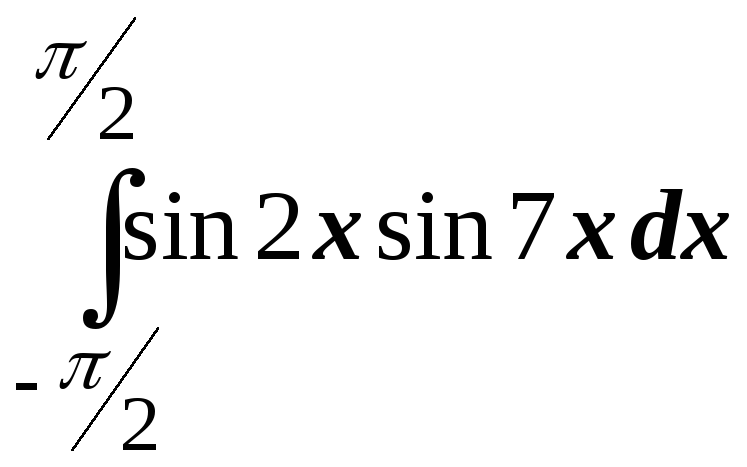 .
.
№8.2. Вычислить интегралы методом подстановки:
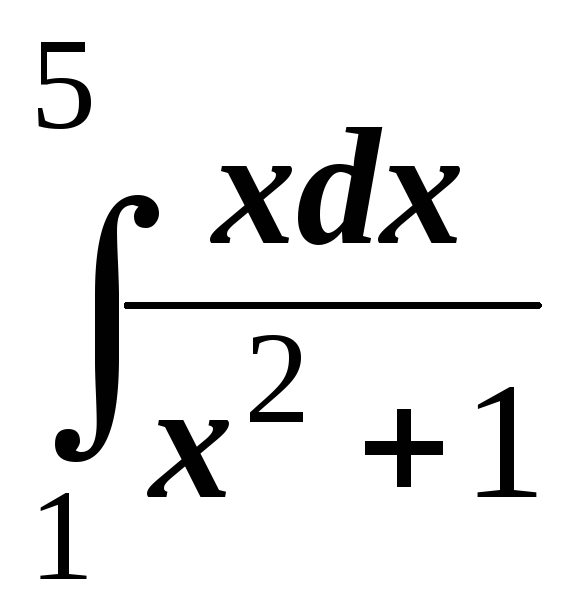 ;
;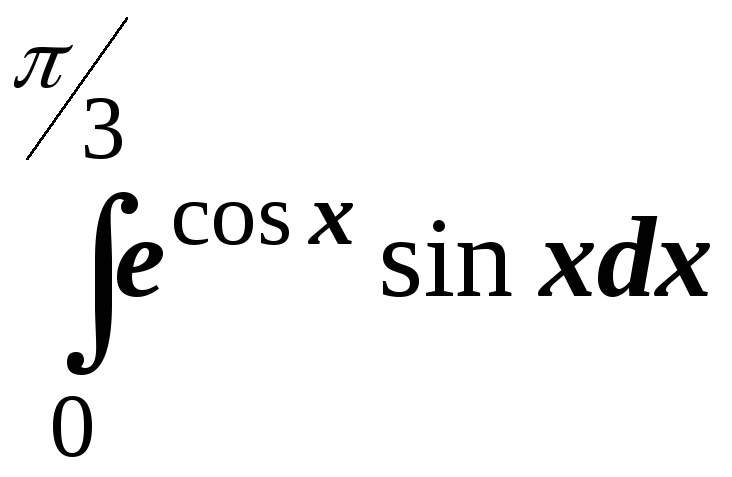 ;
;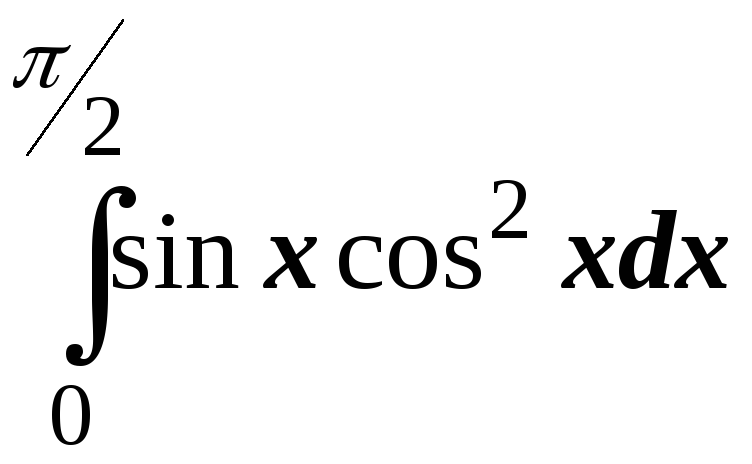 ;
;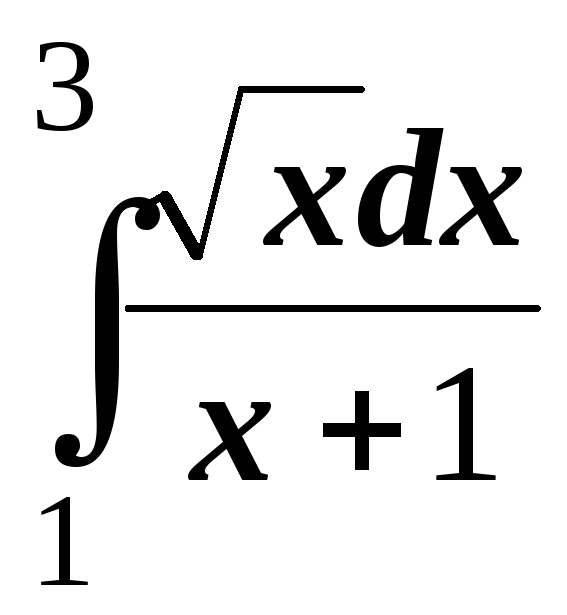 ;
; ;
;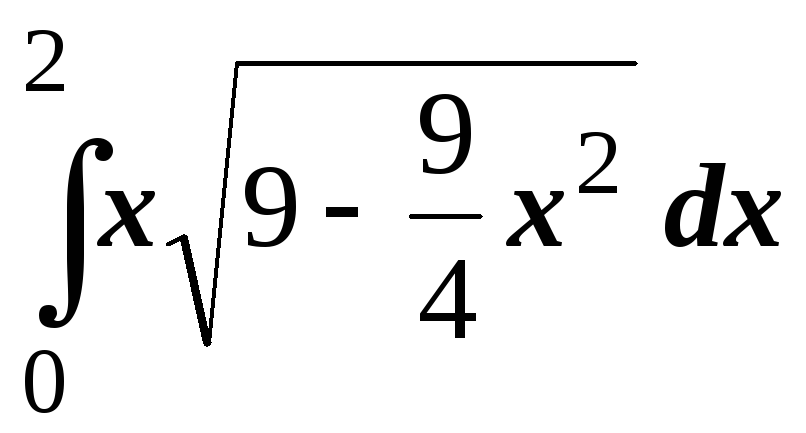 ;
;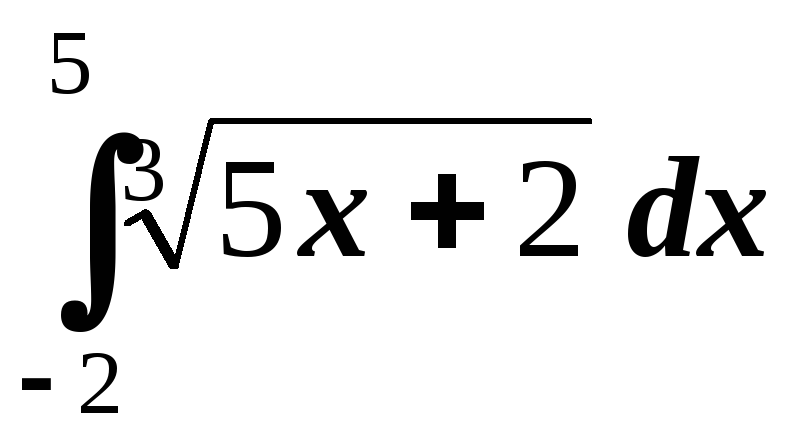 ;
;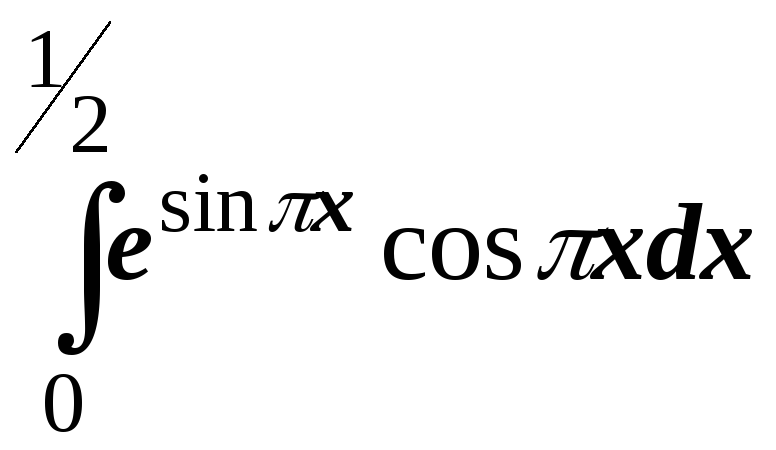 ;
;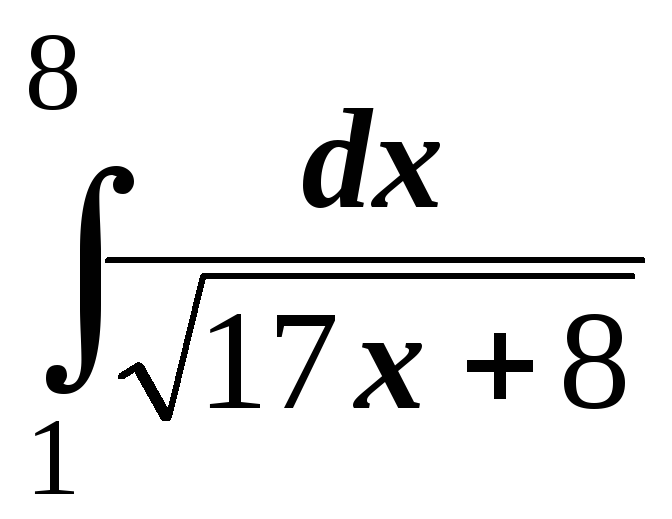 .
.
№8.3. Вычислить интегралы интегрированием по частям:
 ;
;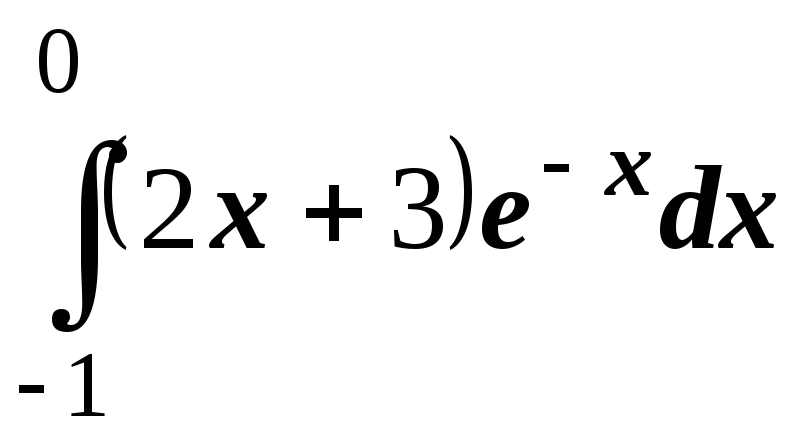 ;
;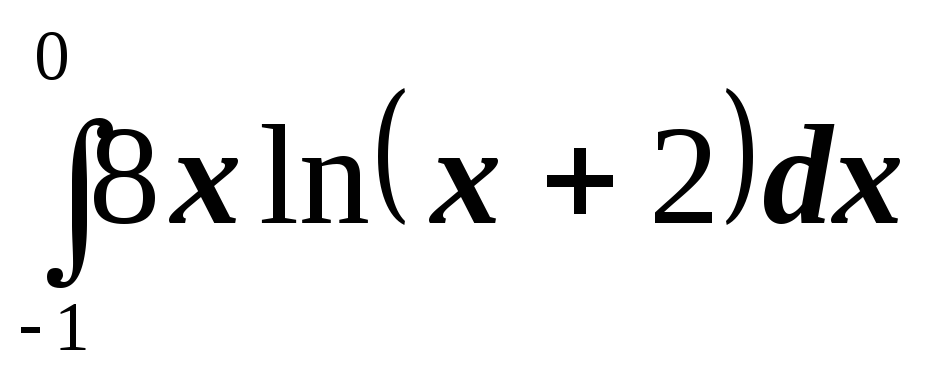 ;
;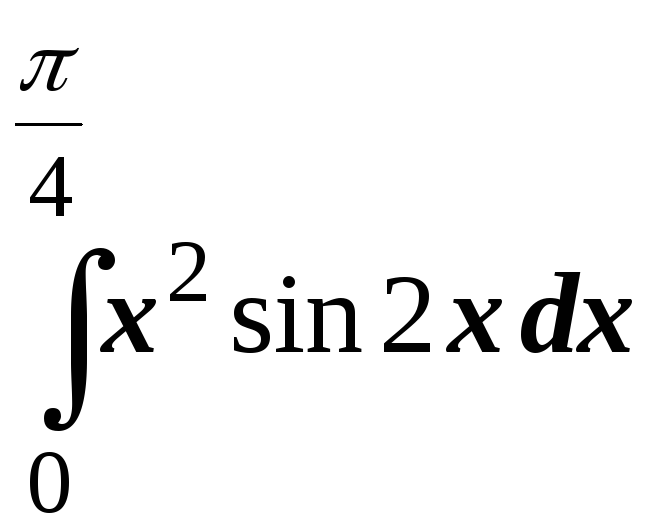 ;
;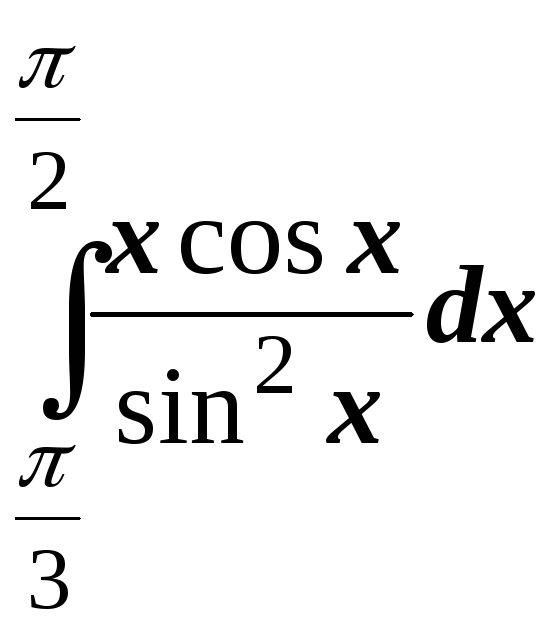 ;
;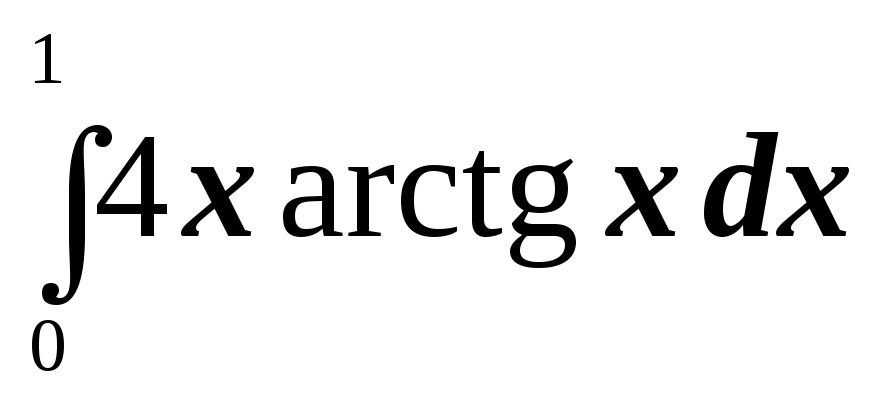 ;
;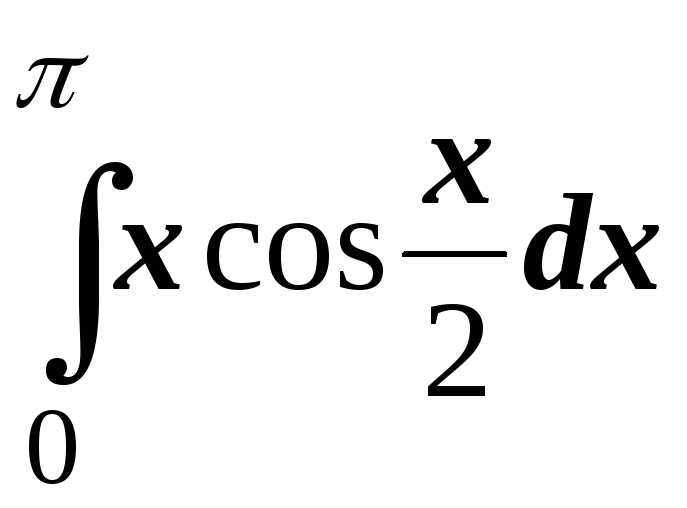 ;
;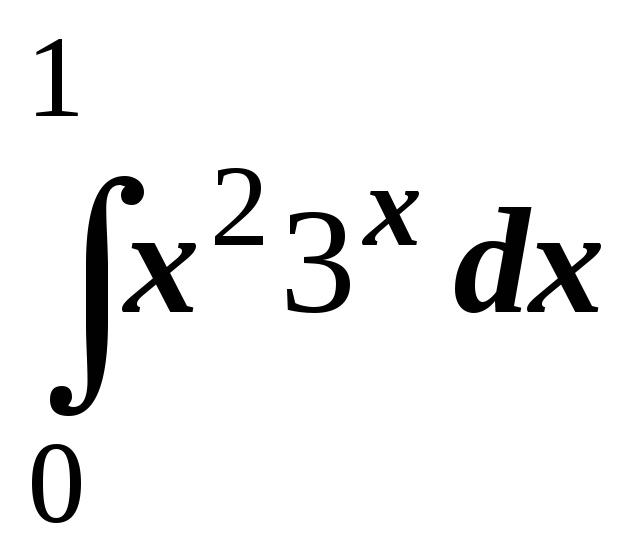 ;
;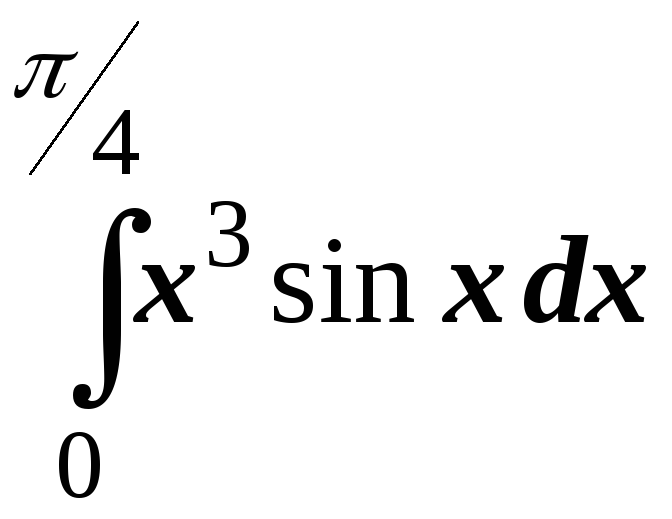 ;
;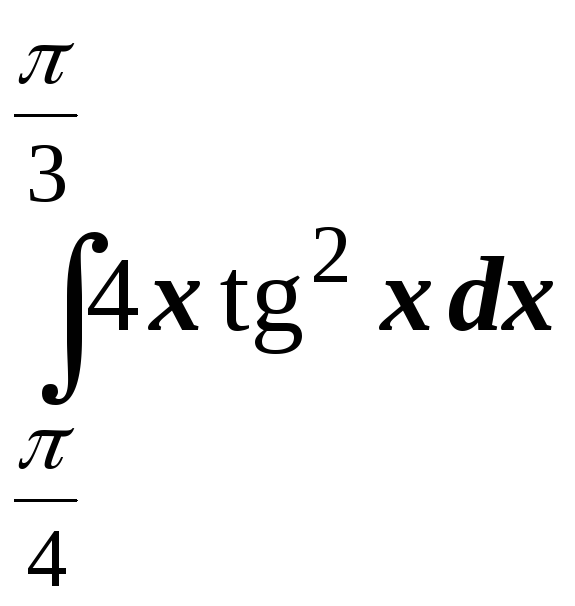 .
.
8.5. Биологические, физические и медицинские приложения определенного интеграла
8.5.1. Примеры задач прикладного характера.
Будем считать численность популяции, биомассу популяции и т.п. непрерывными функциями времени.
Численность популяции. Число особей в популяции (численность популяции) меняется со временем. Если условия существования популяции благоприятны, то рождаемость превышает смертность, и общее число особей популяции растет со временем. Назовем скоростью роста популяции прирост числа особей в единицу времени. Обозначим эту скорость V(t). В “старых”, установившихся популяциях, давно обитающих в данной местности, скорость роста мала и медленно стремятся к нулю. Однако если популяция молода, ее взаимоотношения с другими местными популяциями еще не установились, или существуют внешние причины, изменяющие эти взаимоотношения (например, сознательное вмешательство человека), то V(t) может значительно колебаться, уменьшаясь или увеличиваясь.
Если известна скорость роста популяции, то мы можем найти прирост численности за промежуток времени от t1 до t2. В самом деле, из определения V(t) следует, что она является производной от численности N(t) в момент t, и, следовательно, численность N(t) является первообразной для V(t). Отсюда
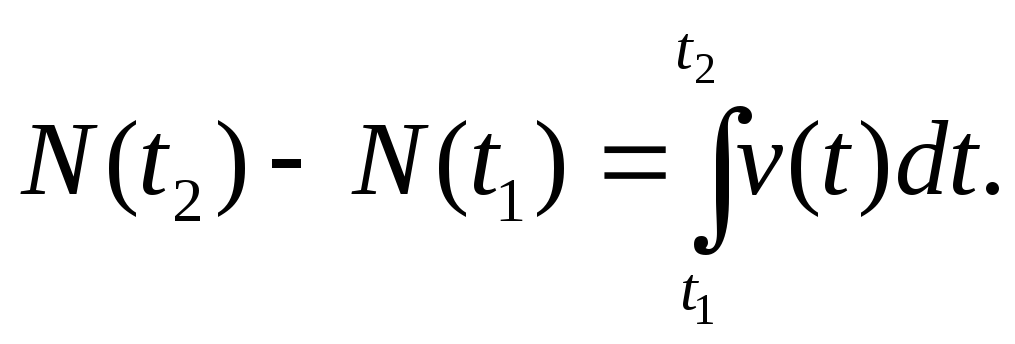 (8.1)
(8.1)
Так, известно, что в условиях неограниченных ресурсов питания скорость роста многих популяций экспоненциальна: V(t)=aert. Популяция в этом случае как бы “не стареет”. Такие условия можно создать, например, для микроорганизмов, пересаживая время от времени развившуюся культуру в новые емкости с питательной средой. В этом случае получим
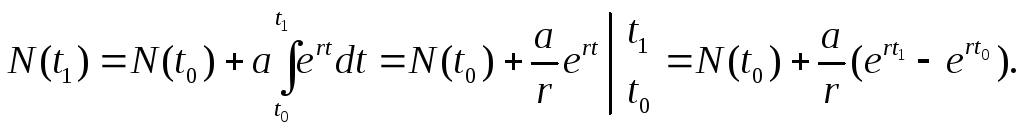 (8.2)
(8.2)
По формуле, подобной (8.2), подсчитывают, в частности, численность культивируемых плесневых грибков, выделяющих пенициллин.
Биомасса популяции. Рассмотрим популяцию, в которой вес особи заметно меняется в течение жизни, и подсчитаем общую биомассу популяции.
Пусть означает возраст в тех или иных единицах времени, а N() – число особей популяции, возраст которых равен . Пусть, наконец Р() – средний вес особи возраста , а М() – биомасса всех особей в возрасте от 0 до .
Заметим, что произведение N()P() равно биомассе всех особей возраста , и рассмотрим разность М(+)-М(). Очевидно, что эта разность, равная биомассе всех особей в возрасте от до +, удовлетворяет неравенствам
![]() (8.3)
(8.3)
где
N(![]() )P(
)P(![]() )
– наименьшее, аN(
)
– наименьшее, аN(![]() )P(
)P(![]() )
– наибольшее значения функцииN()P()
в промежутке [,+].
)
– наибольшее значения функцииN()P()
в промежутке [,+].
Поэтому можно записать, что
![]()
где Т – максимальный возраст особи в данной популяции. Так как М(0), очевидно, равна нулю, то окончательно получаем
![]()
Средняя длина полета. В некоторых исследованиях необходимо знать среднюю длину пробега, или среднюю длину пути при прохождении животным некоторого фиксированного участка. Мы приведем соответствующий расчет для птиц. Пусть участком будет круг радиуса R. Будем считать, что R не слишком велико, так что большинство птиц изучаемого вида пересекают этот круг по прямой.
Птица может под любым углом в любой точке пересечь окружность. В зависимости от этого длина ее пролета над кругом может быть равной любой величине от 0 до 2R. Нас интересует средняя длина пролета. Обозначим ее l.
Так как круг симметричен относительно любого своего диаметра, нам достаточно ограничится теми птицами, которые летят в каком-нибудь одном направлении (например, в направлении, параллельном оси Оу). Тогда средняя длина пролета – это просто среднее расстояние между дугами АСВ и АС1В. Иными словами, это среднее значение функции f1(x)-f2(x), где y=f1(x) – уравнение верхней дуги, а y=f2(x) – уравнение нижней дуги, т.е.
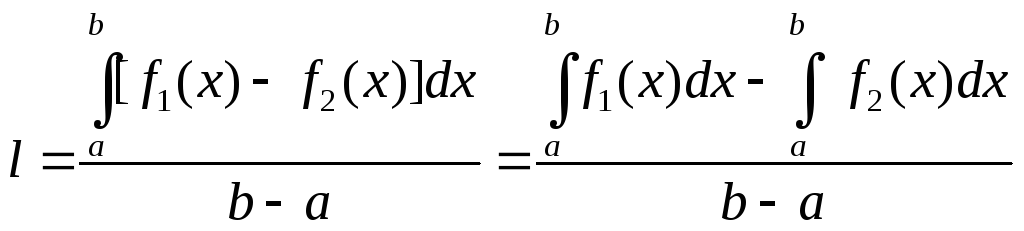 (8.4)
(8.4)
Т
x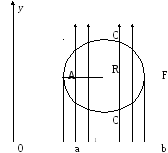
![]() равен
равен
п лощади
криволинейной трапецииaACBb,
а
лощади
криволинейной трапецииaACBb,
а
![]() равен площади трапецииaAC1Bb,
то их разность равна площади круга,
т.е. R2.
Разность b-a
равна, очевидно 2R.
Подставив это в (8.4), получим
равен площади трапецииaAC1Bb,
то их разность равна площади круга,
т.е. R2.
Разность b-a
равна, очевидно 2R.
Подставив это в (8.4), получим
Рис.8.1
14![]()