
- •Рязань 2009
- •Глава 1. Предел функции
- •1.1. Определение предела
- •1.2. Операции над пределами
- •1.3. Замечательные пределы
- •1.4. Примеры
- •1.5. Варианты заданий
- •1.6. Контрольные вопросы Глава 2. Производная и дифференциал
- •2.1 Понятие производной
- •2.2. Геометрический и физический смысл производной
- •2.3. Таблица производных
- •2.4. Основные правила дифференцирования
- •2.5. Производные высших порядков
- •2.6. Дифференциал функции
- •2.7. Геометрический смысл и свойства дифференциала
- •2.8. Дифференциалы высших порядков
- •2.9. Примеры
- •2.10. Варианты заданий
- •2.11. Контрольные вопросы
- •Глава 3. Исследование функций и построение графиков
- •3.1. Промежутки монотонности и знакопостоянства
- •3.2. Экстремумы функции
- •3.3. Выпуклость и вогнутость функции. Точка перегиба
- •3.4. Асимптоты
- •3.5.Общая схема исследования функции и построение графиков
- •3.6. Примеры
- •3.7. Варианты заданий
- •3.8. Контрольные вопросы
- •Глава 4. Функции нескольких переменных
- •4.1. Определение функции нескольких переменных
- •4.2. Частные производные
- •4.3. Полный дифференциал
- •4.5. Примеры
- •4.6. Варианты заданий
- •4.7. Контрольные вопросы Глава 5. Численное дифференцирование
- •5.1. Формулы для вычисления первой производной
- •5.2. Формулы второй производной
- •5.3. Примеры
- •5.4. Варианты заданий
- •5.5. Контрольные вопросы Глава 6 Основы интерполяции.
- •6.1. Постановка задачи
- •Интерполяционные формулы конечных разностей
- •6.3. Интерполяционные формулы центральных разностей
- •6.4. Интерполирование функции с не равноотстоящими узлами
- •6.5. Варианты заданий
- •6.6. Контрольные вопросы Глава 7. Неопределенный интеграл
- •7.1. Первообразная функция и неопределенный интеграл
- •7.2. Основные свойства неопределенного интеграла
- •7.3. Таблица простейших интегралов
- •7.4. Основные методы интегрирования
- •7.4.1. Непосредственное интегрирование
- •7.4.2. Метод подстановки (замена переменной)
- •7.4.3. Интегрирование по частям
- •7.5. Примеры
- •7.6. Варианты заданий
- •7.7. Контрольные вопросы
- •Глава 8. Определенный интеграл
- •8.1. Основные понятия и свойства определенного интеграла
- •Свойства определенного интеграла
- •8.2. Основные методы интегрирования
- •8.2.1. Формула Ньютона-Лейбница
- •8.2.2. Метод подстановки
- •8.2.3. Интегрирование по частям
- •8.3. Примеры
- •8.4. Варианты заданий
- •8.5. Биологические, физические и медицинские приложения определенного интеграла
- •8.5.1. Примеры задач прикладного характера.
- •8.5.2. Примеры решения задач.
- •8.5.3. Варианты заданий
- •Глава 9. Численное интегрирование
- •9.1. Формула прямоугольников
- •9.2. Формула трапеций
- •9.3. Метод средних
- •9.4. Формула Симпсона
- •9.5. Примеры
- •9.6. Варианты заданий
- •9.7. Контрольные вопросы
- •Глава 10. Дифференциальные уравнения
- •10.1. Основные определения
- •10.2. Уравнения с разделяющимися переменными
- •10.3. Однородные уравнения первого порядка
- •10.4. Линейные уравнения первого порядка
- •9.5. Примеры
- •I. Метод Лагранжа
- •II. Метод Бернулли
- •1) Метод вариации произвольной постоянной
- •2) Метод подстановки
- •10.6. Варианты заданий
- •10.7. Применение дифференциальных уравнений в биологии и медицине.
- •10.8. Варианты заданий
- •10.9. Контрольные вопросы
- •Глава 11. Численные методы решения дифференциальных уравнений
- •11.1. Метод Эйлера
- •10.2. Метод Рунге – Кутта
- •10.3. Примеры
- •11.4. Варианты заданий
- •11.4. Контрольные вопросы
- •Глава 12. Элементы теории вероятностей
- •12.1. Случайное событие
- •12.2. Комбинаторика
- •12.3. Вероятность случайного события
- •Закон сложения вероятностей
- •12.5. Варианты заданий
- •12.6. Условная вероятность, закон умножения вероятностей
- •12.7. Варианты заданий
- •12.8. Формулы полной вероятности и Байеса
- •12.9. Варианты заданий
- •11.10. Формулы Бернулли, Пуассона и Муавра-Лапласа
- •12.11. Варианты заданий
- •12.2. Случайные величины
- •12.2.1. Закон распределения случайной величины
- •12.2.2. Функция распределения случайных величин
- •12.2.3. Числовые характеристики дискретной случайной величины
- •12.2.4. Плотность вероятности непрерывных случайных величин
- •12.2.5. Нормальный закон распределения
- •12.3. Варианты заданий
- •Глава 13. Статистический анализ результатов исследований
- •13.1. Основные понятия математической статистики
- •13.1. Варианты заданий
- •13.2. Статистические оценки параметров распределения. Выборочные характеристики
- •13.2.1. Характеристики положения
- •13.2.2. Характеристики рассеяния вариант вокруг своего среднего
- •13.3. Варианты заданий
- •13.4. Оценка параметров генеральной совокупности по ее выборке
- •13.4.1. Точечная оценка параметров генеральной совокупности
- •13.5. Варианты заданий
- •13.6. Интервальная оценка параметров генеральной совокупности
- •13.7. Варианты заданий
- •1.8. Контрольные вопросы
- •Глава 14. Корреляционный и регрессионный анализ
- •14.1. Функциональная и корреляционная зависимости
- •14.2. Коэффициент линейной корреляции и его свойства
- •14.3. Проверка гипотезы о значимости выборочного коэффициента линейной корреляции
- •14.4. Выборочное уравнение линейной регрессии. Метод наименьших квадратов
- •14.5. Нелинейная регрессия
- •14.6. Варианты заданий
- •Приложение
- •Критические значения выборочного коэффициента корреляции
- •Критерий Колмогорова – Смирнова Точные и асимптотические границы для верхней грани модуля разности истинной и эмпирической функции распределения
- •Распределение Пирсона (х2– распределение)
- •Распределение Фишера – Снедекора (f-распределение)
- •Библиографический список
- •Содержание
- •Глава 13. Статистический анализ результатов исследований 160
- •Глава 14. Корреляционный и регрессионный анализ 180
5.4. Варианты заданий
№ 5.1. Получить таблицы значений следующих функций на интервале от 1 до 3 с шагом 0,2. Пользуясь безразностными формулами по 4 точкам, найти численные значения первой производной в этих точках, и сравнить полученные значения с аналитическими.
у=ех;
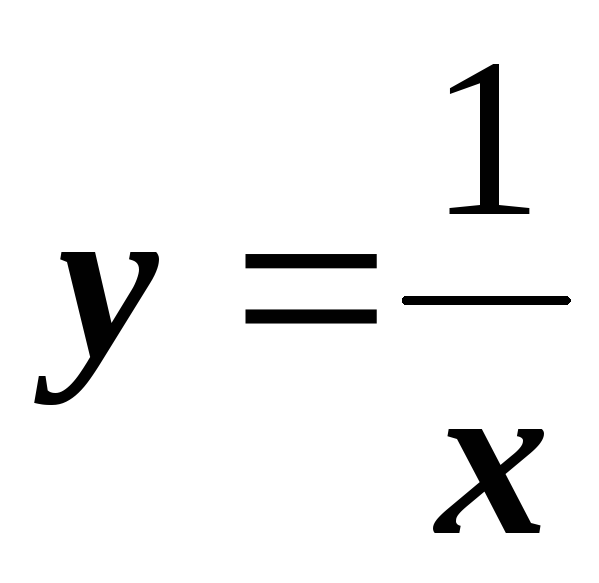 ;
;у=ln x;
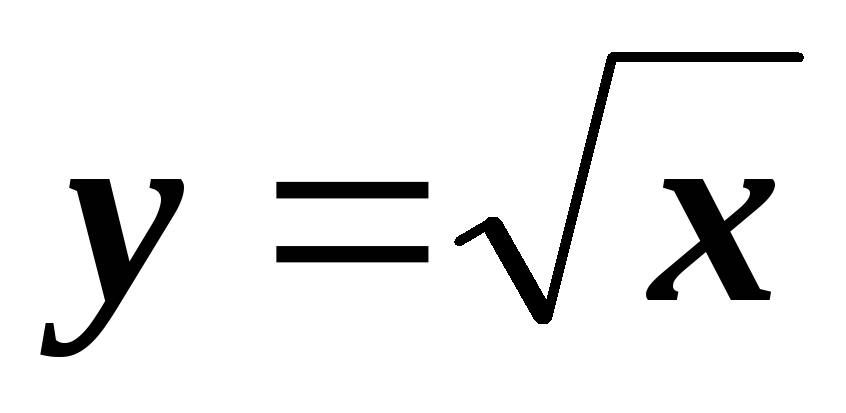 ;
;y=sin x;
y=e2x;
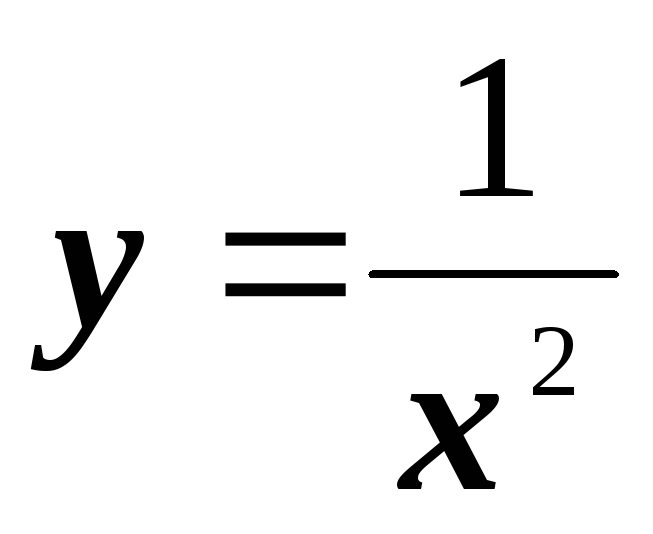 ;
;у=(х–1)2;
y=cos x;
y=ln x2;
№ 5.2. Получить таблицы значений следующих функций на интервале от 1 до 3 с шагом 0,2. Пользуясь безразностными формулами по 3 точкам, найти численные значения первой производной в этих точках, и сравнить полученные значения с аналитическими.
у=sin x;
y=cos x;
y=sin(x2);
y=sin2 x;
y=cos2 x;
y=sin(2x);
y=cos(2x);
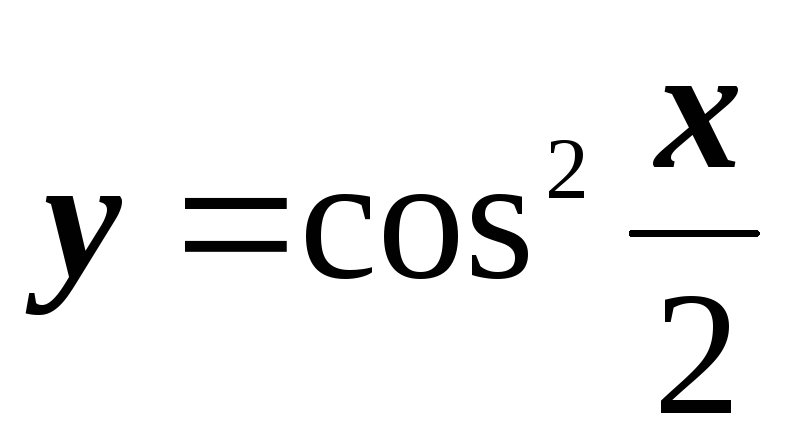 ;
;y=ln2 x;
y=ln3 x;
№ 5.3. Для перечисленных функций, пользуясь безразностными формулами по 4 точкам, найти вторые производные в точках от 1 до 3 с шагом 0,2 и сравнить полученные значения с аналитическими.
y=e2x;
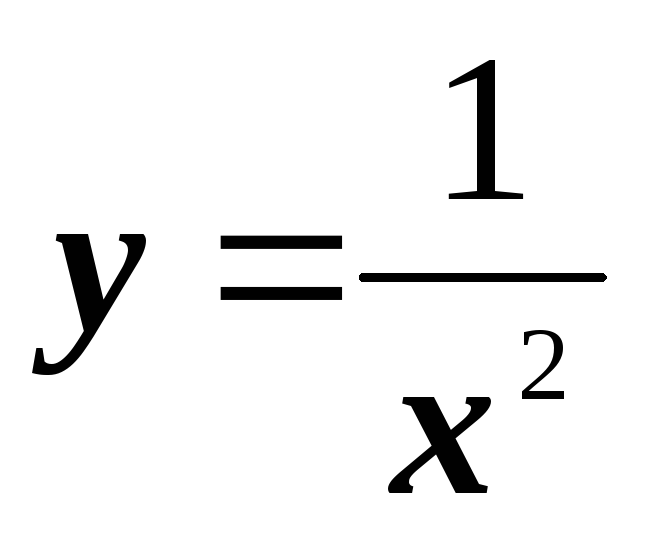 ;
;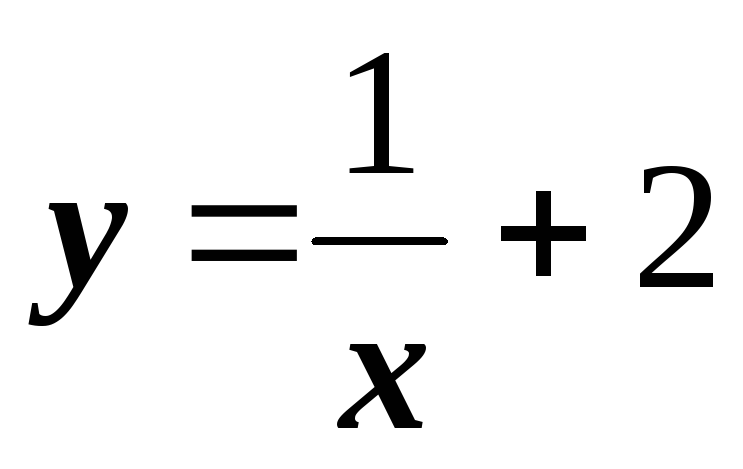 ;
;у=(х–1)2;
y=ln(x2);
y=
 ;
;y=sin2 x;
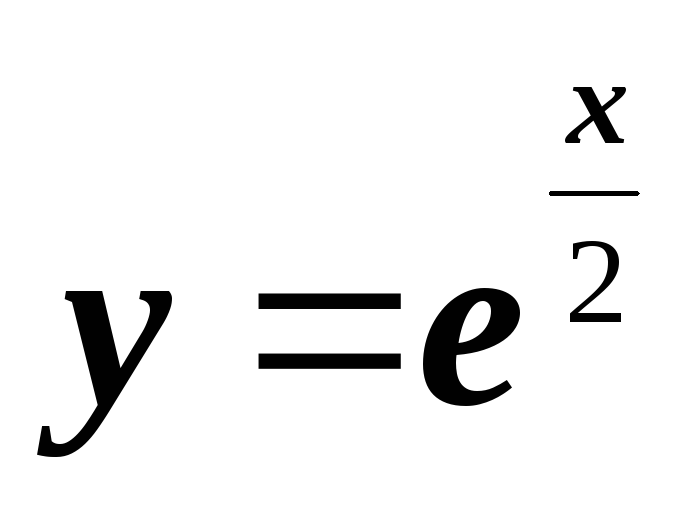 ;
;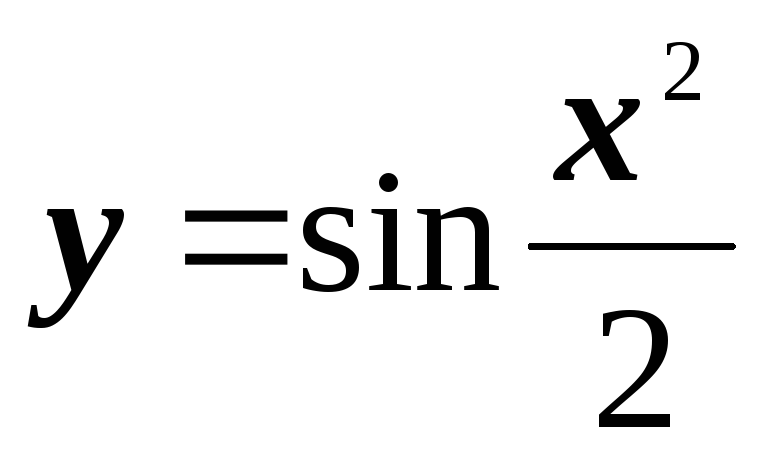 ;
;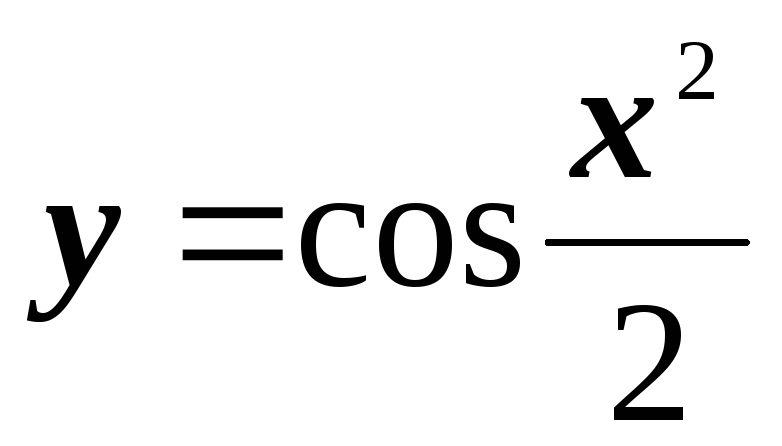 .
.
5.5. Контрольные вопросы Глава 6 Основы интерполяции.
6.1. Постановка задачи
Пусть некоторая функция f(x) задана таблично на интервале [a,b]
f(xn)=yn, f(x1)=y1, ... , f(xn)=yn (6.1) в n+1 точках x0, x1, x2, ... ,xn.
Под интерполяцией понимается нахождение по таблице значений функции её аналитического описания, позволяющего вычислять значение этой функции от аргумента отсутствующего в таблице, т.е. так называемое чтение "между" строк. Задача сводится к построению функции f(x) (интерполирующей функции), принадлежащей известному классу функций и принимающей в точках x0, x1, x2, ... , xn (узлах интерполяции) те же значения, что и функция
f(x0)=y0, f(x1)=y1, ... , f(xn)=yn,
а в остальных точках отрезка [a,b] приближённо представляющая функцию f(x) с какой-то степенью точности.
При этом допускают, что f(x) непрерывна на отрезке [a,b] и имеет на нём в каждой точке конечные производные любого порядка, а узлы интерполирования отличны друг от друга.
Через точки x0, x1, x2 , ... , xn можно провести бесчисленное множество кривых (рис. 6.1). Следовательно, задача отыскания функции f(x) по её значениям, поставленная таким образом, является неопределённой: можно построить бесчисленное множество функций принимающих при x0, x1, x2 , ... , xn, значение y0, y1, y2, ... , yn
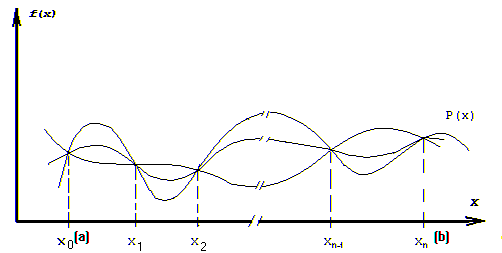
Рис. 6.1
Чтобы получить единственную f(x) наложим на неё дополнительные ограничения, а именно, в качестве f(x) используем полином P(x) степени на единицу меньше числа заданных значений n+1.
Интерполяционные формулы конечных разностей
Для функции f(x), заданной таблично, величина i=yi+1-yi называется первой нисходящей конечной разностью. Величина 2yi=yi+1-yi - второй конечной разностью, а, следовательно, для произвольного порядка будем иметь
nyi=n-1yi+1-n-1yi. (6.2)
Первая восходящая конечная разность определяется из
![]() ,
,
для разности второго порядка имеем формулу
![]()
и аналогично для произвольного порядка получаем
![]() . (6.3)
. (6.3)
Нисходящие разности употребляются в основном в начале таблицы, а восходящие разности в конце её.
Для функции f(x), заданной в равноотстоящих точках, для интерполирования вперёд используется формула Грегори-Ньютона в виде.
![]() (6.4)
(6.4)
где t=(x-x0)/h - число шагов необходимое для достижения точки x, исходя из точки x0; ky0 - нисходящая конечная разность k-го. Погрешность этой формулы, называемой первой интерполяционной формулой Ньютона, определяется из
![]() (6.5)
(6.5)
где x0x.
Полином выгодно использовать в окрестностях начального значения x0, когда t - мало по абсолютной величине.
Если в (6.4) положить n=1, то получим формулу линейного интерполирования
P1(x)=y0+ty0, (6.6)
при n=2 будем иметь формулу квадратичного интерполирования.
![]() .
(6.7)
.
(6.7)
За начальное значение x0 можно принять любое x. Тогда формула (6.4) содержит только те значения y(x), которые идут после этого начального значения.
Если дана неограниченная таблица значений y, то степень полинома n может быть любой и её выбирают из условия, чтобы ny была с заданной степенью точности постоянной.
Формула Грегори-Ньютона для интерполирования назад (вторая интерполяционная формула Ньютона) имеет вид
![]() (6.8)
(6.8)
где t=(x-xn)/h.
Погрешность формулы (6.8) определяют по
![]() ,
(6.9)
,
(6.9)
в
котором
![]() .
.
Формулу рекомендуется применять вблизи конца таблицы. Обе формулы можно использовать для экстраполяции y(x), если она на концах [a,b] изменяется плавно. Шаг экстраполяции берётся h/2.
