
ТеорМЕХ3куПМ
.pdf
41
координат являлись бы независимыми.. Пользуясь такой независимостью, можно принять равными нулю все вариации координат, кроме xj . Тогда в первой сумме останется только
одно слагаемое
(X j m j xj )xj 0
Так как xj |
0 , то должно быть равно нулю выражение в квадратной скобке, которое приводит |
||||||
к уравнению (уравнениям, так как в наших рассуждениях индекс |
j |
не фиксировалcя) |
|||||
|
|
|
mj xj |
X , |
j=1,2,…,3N |
|
|
|
|
|
|
j |
|
|
|
В общем же случае, |
не все x j 0 |
независимые, так как они связаны двумя системами |
|||||
равенств. () и (). Число независимых вариаций координат равно 3 N |
k r .Чтобы в этом случае |
||||||
найти независимые вариации координат можно поступить так. |
Принять например, первые |
||||||
k r вариаций координат |
зависимыми, |
и выразить их через |
|
остальные ( независимые) |
|||
координаты, |
разрешив |
k |
r уравнений связей относительно зависимых вариаций координат. |
||||
Полученные значения подставить в уравнение (), |
и пользуясь независимостью оставшихся |
||||||
вариаций координат получить соответствующие дифференциальные уравнения движения
системы, которые , |
очевидно, будут |
отличаться от уравнений |
() так |
как в них |
будут |
||||
присутствовать |
еще |
и производные |
f |
и коэффициенты a |
. |
Лагранж |
предложил |
более |
|
|
|||||||||
x |
|||||||||
|
|
|
|
|
|
|
|
||
изящный метод |
исключения зависимых вариаций координат, |
основанный на использовании |
|||||||
метода неопределенных множителей, |
|
известного студентам по разделу относительного |
|||||||
экстремума функции |
курсе математического анализа. |
|
|
|
|
||||
Займемся выводом уравнений Лагранжа 1-го рода. Имеем по принципу Даламбера-Лагранжа
|
3N |
|
|
|
|
|
|
|
|
(Xν |
|
mν xν )δxν |
0 |
|
|||
|
ν 1 |
|
|
|
|
|
|
|
Каждое из уравнений () умножаем |
на |
соответствующий множитель |
и суммируем |
|||||
полученные равенства по всем |
. Получаем.равенство |
|
||||||
|
k |
|
3N |
f χ |
|
|
|
|
|
|
|
|
|
|
|||
|
λ |
χ |
|
|
|
δx |
0 |
|
|
|
|
|
|
||||
|
|
|
|
xν |
ν |
|
|
|
|
χ 1 |
|
ν 1 |
|
|
|
||
Меняем порядок суммирования, что дает
3N k
 1
1  1
1
f
x
x 0
Аналогично, каждое из уравнений () умножаем на соответствующий множитель 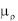 суммируем полученные равенства по всем
суммируем полученные равенства по всем  , и меняем порядок суммирования
, и меняем порядок суммирования
|
3N |
r |
|
|
|
|
|
|
|
|
a |
x |
0; |
|
1 |
|
1 |
|
|
|
Складываем равенства () , () и (). |
|
|
|
|
|
|
3N |
|
k |
|
f χ |
r |
|
|
|
|
|
|||
{X ν |
mν xν |
|
λχ |
|
|
μχ aρ ν } δxν 0 |
|
xν |
|
||||
ν 1 |
χ |
1 |
|
χ |
1 |
|
Выберем значения k+r множителей Лагранжа  и
и  таким образом, чтобы выражения в фигурных скобках при k+r зависимых вариациях координат обратились в ноль. Тогда в силу
таким образом, чтобы выражения в фигурных скобках при k+r зависимых вариациях координат обратились в ноль. Тогда в силу

42
независимости остальных 3N-k-r вариаций координат выражения в фигурных скобках также должны быть равны нулю, что приводит к системе уравнений Лагранжа 1 рода
|
|
|
|
|
|
f χ |
|
|
|
|
|
k |
|
|
|
|
r |
|
|
mν xν |
Хν |
|
λχ |
|
|
|
|
μρaρ ν |
ν 1,...,3N |
|
|
|
xν ρ 1 |
||||||
|
|
χ |
1 |
|
|
|
|
||
которые совместно с уравнениями связей |
|
|
|
|
|
|
|||
f χ (x1 ,...,x3N ,t) |
0,χ |
1,...,k |
|
|
|||||
3N |
|
|
|
|
|
|
|
|
|
aρ ν xν |
aρ , ρ |
|
|
1,2,...,r |
|
||||
λ 1 |
|
|
|
|
|
|
|
|
|
образуют замкнутую систему 3N |
k |
r |
уравнений для определения 3N k r неизвестных: |
||||||
x ν ( ν 1,...,3N), λχ ( χ |
1....,k ) |
и μρ |
( |
|
1,...,r ) . |
|
|||
Вэтих уравнениях:
Хν - внешние активные силы, действующие на систему,
λχ |
f χ |
- силы реакций соответствующих голономных связей, |
|
xν |
|||
|
|
μρ aρν - силы реакций соответствующих неголономных связей,
Достоинства и недостатки Уравнений Лагранжа 1 рода. Достоинства:
Описывается движение механической системы с любым количествтом материальных точек и связей,
Учитываются не только голономные, но и неголоно, мные связи. Можно определить величины реакций связей Можно определить движение каждой точки системы.
Недостатки Большое число уравнений, которые надо решать.
С увеличением количества связей увеличивается число уравнений, подлежащих решению.
Уравнения Лагранжа 2 рода.
Перечисленных выше недостатков лишены уравнения Лагранжа 2 рода. Обратим внимание на то, что с увеличением количества связей свободы движения для точек системы уменьшается. Уменьшается число степеней свободы, которое для одной материальной точки равно 3, для абсолютно твердого тел – 6, для абсолютно твердого тела с одной неподвижной точкой – 3. За число степеней свободы системы можно принять число независимых вариаций координат. Если на систему наложены только к геометрических (голономных) связей, то число степеней свободы для такой системы будет равно n= 3N-k. Столько же будет у такой системы независимых координат.
Обобщенные координаты.
Положение точек и абсолютно твердых тел в системе не обязательно определять в декартовой системе координат, особенно в случаях, когда на систему наложены геометрические связи. Бывает более удобным определять положение системы другими величинами. Например, для абсолютно твердого тела с неподвижной осью вращения , нами положение этой системы материальных точек определялось только одним параметром - углом
В общем случае обобщенные координаты вводятся как не зависимые между собой величины, являющиеся только функциями времени и полностью определяющие положение
43
системы в любой момент времени..Их число равно числу степеней свободы системы. Они обозначаются так
q1 ,q2 , ,...,qn
Координаты всех точек системы при этом должны быть только функциями этих координат и времени
xν xν (q1 ,q2 , ,...,qn ,t).ν 1,...,3N
Изохронные вариации этих координат равны
n |
xν |
|
|
xν |
q j |
||
q j |
|||
j 1 |
|
Подставляем эти вариации в принцип ДаламбераЛагранжа
3N |
n |
xν |
|
|
|
(X ν mν xν ) |
|
q j |
0 |
||
j 1 q j |
|||||
ν 1 |
|
|
|||
Это уравнение удобно переписать так
n 3N |
|
xν |
3N |
|
xν |
|
|
|
( m x |
X |
|
) q |
|
0 |
|||
|
|
|
||||||
j 1 ν 1 |
ν |
q j |
ν 1 |
νν q j |
j |
j |
||
|
|
|
|
|
|
|
|
|
В силу независимости вариаций обобщенных координат имеем равенства
3N |
|
|
xν |
|
mν x |
||||
q j |
||||
ν 1 |
|
|
||
Введем обозначения |
|
|
|
|
3N |
|
|
xν |
|
X |
|
|
||
νν |
q j |
|||
ν 1 |
|
|
||
Преобразуем теперь выражение
3N |
xν |
|
|
X ν ν |
0, j 1,2..,,n |
||
q j |
|||
ν 1 |
|
Qj - обобщенные силы.
|
xν |
. Можно записать |
|
||
x |
q j |
|
|
|
x |
|
xν |
|
|
dx |
|
|
xν |
|
|
|
d |
( x |
|
|
xν |
) x |
d |
|
xν |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
q j |
dt q j |
|
|
dt |
|
|
|
|
|
q j |
|
|
|
dt q j |
|
|
|
||||||||||||||||||||
Имеют место равенства Лагранжа, которые нетрудно проверить |
|||||||||||||||||||||||||||||||||||||||
|
|
|
xν |
|
|
|
|
xν |
|
d xν |
xν |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
q j |
|
|
|
|
q j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
dt q j |
q j |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Проверка справедливости равенств Лагранжа. Учтем, что xν |
|
dx |
|||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||
|
dt |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
dx |
n |
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||||||||||||
Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Дифференцирование |
|
|
|
|
|
|
|
dt |
i 1 |
qi |
|
|
t |
|
|
|
|
|
q j подтверждает справедливость |
||||||||||||||||||||
|
|
этих равенств |
|
|
по переменной |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
первого равенства Лагранжа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Дифференцированием этих равенств по переменной q j |
получаем равенство |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
n |
2 x |
q |
|
|
2 x |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
q j |
i 1 qi q j |
i |
|
|
t q j |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||

|
|
|
|
44 |
|
|
|
|
|
|
С другой стороны, полная производная по времени от функции |
xν |
имеет вид |
||||||||
|
||||||||||
|
|
|
|
|
|
|
|
|
q j |
|
|
d x |
n 2 x |
qi |
2 x |
|
|
||||
|
|
|
ν |
|
|
|
|
|
|
|
|
dt q j |
i 1 qi q j |
t q j |
|
|
|||||
|
|
|
|
|||||||
Так как правые части последних двух равенств совпадают, то должны совпадать и левые их части, чем и подтверждается справедливость второго равенства Лагранжа.
В силу равенств Лагранжа формула |
() преобразуется к виду |
|||||||||
x |
xν |
|
d |
|
( x |
xν |
) |
x |
xν |
|
|
|
|
|
|
|
|
||||
|
q j |
|
dt |
q j |
|
q j |
||||
которую удобно представить в такой форме |
|
|
|
|||||||
x |
x |
|
d |
|
x 2 |
|
|
x 2 |
||||
ν |
|
|
[ |
|
( |
|
)] |
|
( |
|
) |
|
q j |
|
dt |
q j |
2 |
q j |
2 |
||||||
Умножая полученные равенства на соответствующие величины масс точек mν и суммируя получаемые при этом соотношения по всем ν , получаем
3N |
x |
x |
|
d |
|
|
3N m x 2 |
|
|
3N |
m x 2 |
|
mν |
ν |
|
|
( |
|
|
ν |
) |
|
|
ν |
|
q j |
|
dt |
q j ν 1 |
2 |
q j ν 1 |
2 |
||||||
ν 1 |
|
|
|
|
||||||||
.Суммы, стоящие па правых частях равенств, равны кинетической энергии системы (по определению). Поэтому можно записать
|
|
|
3N |
|
|
|
|
|
xν |
|
|
d |
|
T |
|
T |
|
|
|
|
|
|
|||||||||||
|
|
|
ν 1 mν xν |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ν ( |
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
q j |
dt |
|
q j |
|
q j |
|
|
|
|
|
|
||||||||||||||||||
Уравнения () при этом принимают вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
d |
|
( |
|
T |
|
) |
|
T |
|
|
|
Qj , j |
1,2,...,n |
|
||||||||||||||||
|
|
|
dt ν |
|
q j |
q j |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Эти уравнения называются уравнениями Лагранжа. 2 |
рода |
|
|||||||||||||||||||||||||||||
|
|
В случае потенциальных сил, когда существует |
такую функцию обобщенных координат |
||||||||||||||||||||||||||||||
U(q |
1 ,q2 ,...,qn ),что |
|
|
|
|
|
|
Qj |
|
|
|
|
|
U |
, j |
|
1,2,...,n |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
j |
|
|
|
|
|
|
|
|
|
||||
то |
М1 |
|
|
|
|
|
|
такую |
|
функцию называют потенциалом силового |
|||||||||||||||||||||||
поля. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
прямой путь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Уравнения Лагранжа 2 рода при этом преобразуются |
||||||||||||||||||||||
к виду |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
окольный путь |
|
|
|
|
|
d |
( |
|
|
T |
) |
|
T |
|
|
U |
, j 1,2,...,n |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
М0 |
|
|
|
|
|
|
|
dt |
|
ν |
q j |
|
q j |
|
|
q |
j |
|
|||||||||||||
В |
|
|
|
|
|
|
этом случае удобно ввести в рассмотрение функцию |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
Рис. |
|
|
|
|
|
|
(функцию Лагранжа) |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
L |
|
|
T |
U |
|
|
|
|
|
|
|
|
|
|||||||||||
для |
|
|
|
|
|
|
которой справедливы уравнения |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
( |
|
|
L |
) |
|
L |
0 , j |
1,2,...,n |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
ν |
q j |
|
q j |
|
|
|
|
|
|
||||||||||
Вариационный интегральный принцип Гамильтона-Остроградского

45 |
|
Принцип Гамильтона-Остроградского |
(принцип стационарного действия)- |
общий интегральный вариационный принцип классической механики, установлен в середине 19 века У.Гамильтоном для голономных систем, на которые наложены только идеальные стационарные связи и обобщен М. В. Остроградским на нестационарные связи. Введено понятие действия по Гамильтону
S |
t1 L(q, q,t)dt |
|
t0 |
Принцип Гамильтона-Остроградского
Действие по Гамильтону имеет стационарное значение для действительных перемещений системы (по прямым пулям) из начального положения в другое по сравнению с близкими кинематически возможными движениями (по окольным п утям), для которых начальное и конечное положения системы и время движения одинаковы с таковыми для действительного движения.
В большинстве случаев истинное движение доставляет функционалу S наименьшее значение. Поэтому принцип Гамильтона-Остроградского часто называют принципом наименьшего действия. Математически принцип Гамильтона-Остроградского формулируется так: для истинного движения при сформулированных выше условиях необходимо и достаточно, чтобы
S 0 |
или |
t1 L( q,q,t )dt 0 |
|
|
t0 |
Это задача вариационного исчисления. Из теории вариационного исчисления следует, что для того , чтобы последнее условие выполнялось, необходимо и достаточно, чтобы функции q( t ) удовлетворяли уравнениям Эйлера
L |
|
d |
( |
L |
) 0 , j 1,2,...,n , |
|
|
|
|
||
q j |
|
dt |
|
q j |
|
и заданным начальным и конечным условиям.
Как видно, уравнения Эйлера совпадают с уравнениями Лагранжа 2 рода..
Важно отметить, что согласно |
принципа |
Гамильтона- |
|
|
Остроградского достаточно минимизировать функцию |
|
|||
Гамильтона (функционал), для чего не обязательно решать |
|
|||
уравнения |
Лагранжа 2 рода, |
а можно |
использовать |
|
численные методы минимизации функционалов. |
|
|
||
Движение абсолютно твердого тела с одной неподвижной |
|
|||
точкой. |
|
|
|
|
Так как тело абсолютно твердое, то с ним можно связать |
|
|||
подвижное пространство, а с пим –подвижную систему |
|
|||
координат: |
|
|
|
|
(ξ, η, ζ) – неподвижная система координат; |
|
|
||
(x, y, z) – подвижная система координат; С – центр масс тела. |
Рис. |
|||
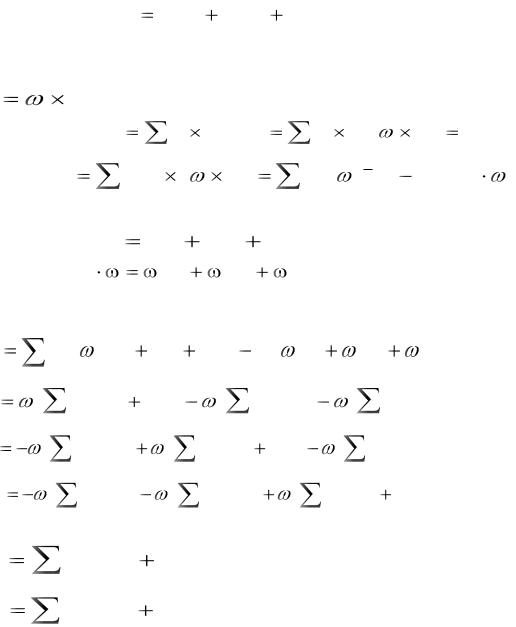
46
Для изучения движения тела можно использовать как на подвижные, так и на неподви жные
оси.
Вектор  (t) – мгновенная угловая скорость. Он выходит из начала координат. Его можно проецировать как на подвижные, так и на неподвижные оси.
(t) – мгновенная угловая скорость. Он выходит из начала координат. Его можно проецировать как на подвижные, так и на неподвижные оси.
Движение тела как систему материальных точек можно изучать, используя общие теоремы механики (теорема о движении центра масс, теорема о кинетическом моменте, теорема о кинетической энергии).
Кинетический момент абсолютно твердого тела с одной неподвижной точкой.
Принимаем неподвижную точку за начало подвижной системы координат Определим кинетический момент тела относительно неподвижной точки О. Будем его находить в проекциях на подвижные оси координат:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G xo |
G yo |
|
G zo |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
o |
|
|
|
|
x |
|
|
y |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пусть масса к-той материальной точки тела равна mk |
а радиус – вектор этой точки равен |
|
|
||||||||||||||||||||||||||||||||||||||||
rk , а |
|||||||||||||||||||||||||||||||||||||||||||
скорость этой точки равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
vk . Согласно формуле Эйлера имеем |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
vk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
rk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
Go |
|
|
|
|
|
|
(mk vk ) |
|
|
|
|
(mk |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
rk |
|
|
rk |
|
rk ) |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
mk |
|
( |
|
|
|
|
|
[mk |
|
|
(rk 2 ) mk |
|
|
|
|
|
)] , |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
rk |
|
rk ) |
|
|
|
rk (rk |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
x |
2 |
|
|
y 2 |
z |
2 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
k |
|
|
k |
k |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x xk |
y yk |
|
z zk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
rk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
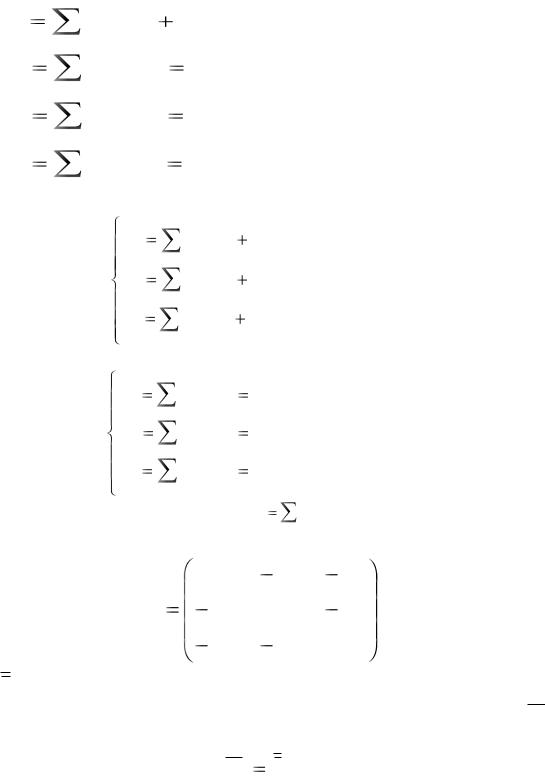
Gx - проекция вектора на ось Ox.
|
|
|
[m |
|
(x 2 |
y 2 |
z 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
G |
) |
|
( |
x |
|
|
y |
|
|
z |
|
)] |
||||||||||||||
|
|
r |
|
|
|
z |
k |
|||||||||||||||||||
|
|
O |
|
k |
|
k |
k |
|
k |
|
|
|
k |
x k |
|
y k |
|
|
|
|
||||||
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
x |
m (y 2 |
z 2 |
) |
y |
|
|
m x y |
|
z |
|
m x z |
k |
|
||||||||||||
|
|
x |
|
k |
|
k |
k |
|
|
|
|
|
k k k |
|
|
k k |
|
|
||||||||
|
|
|
|
k |
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
G |
y |
x |
m y x |
y |
|
m (x |
2 |
|
|
z 2 ) |
z |
|
m y z |
k |
|
|
|
|
||||||||
|
|
|
k k k |
|
k |
k |
|
|
|
|
k |
|
k k |
|
|
|
|
|||||||||
|
|
|
|
|
k |
|
|
|
k |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
G |
x |
m z x |
y |
m z |
y |
k |
z |
m (x |
2 |
y 2 |
) |
|
|
|
|||||||||||
|
|
|
z |
|
|
k k k |
k k |
|
k |
k |
k |
|
|
|
|
|
||||||||||
|
|
|
|
|
k |
|
|
|
k |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
Введем обозначения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
I |
xx |
|
m (y 2 |
z |
2 |
); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
k |
|
k |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
yy |
|
m (x 2 |
z |
2 |
); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
k |
|
k |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
k
47
I |
zz |
m (x 2 |
y 2 |
); |
|
|
|
|
|
||||
|
k k |
k |
|
|
|
|
|
|
|
||||
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
I xy |
mk xk yk |
I yx ; |
|
|
|
|
|
||||||
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
I xz |
mk xk zk |
I z x ; |
|
|
|
|
|
||||||
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
I yz |
mk yk zk |
I z y |
|
|
|
|
|
|
|
||||
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
xx |
m (y |
2 |
z |
2 |
) |
|
|
|||
|
|
|
k |
|
k |
|
k |
|
|
|
|||
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
I |
yy |
m (x |
2 |
z |
2 |
) |
|
|
|||
|
|
|
k |
|
k |
|
k |
|
- осевые моменты инерции |
||||
|
|
|
|
|
|
k |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
zz |
m (x |
|
2 |
y |
2 |
) |
|
|
||
|
|
|
k |
k |
|
k |
|
|
|
||||
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
I xy |
mk xk yk |
I yx |
|
|
|
||||||
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
I xz |
mk xk zk |
I zx |
= центробежные моменты инерции |
||||||||
|
|
|
|
|
|
k |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I yz |
mk yk zk |
I zy |
|
|
|
||||||
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
Эти величины наряду с массой тела |
M |
mk |
являются динамическими характеристиками |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
тела. Они образуют тензор инерции тела |
|
|
|
||||||||||
|
|
|
|
|
|
I xx |
|
|
I xy |
|
I xz |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
I xy |
|
I yy |
|
I yz |
|||||
|
|
|
|
|
|
I xz |
|
|
I yz |
|
I zz |
||
I - тензор инерции. Он определяет инерционные свойства тела.
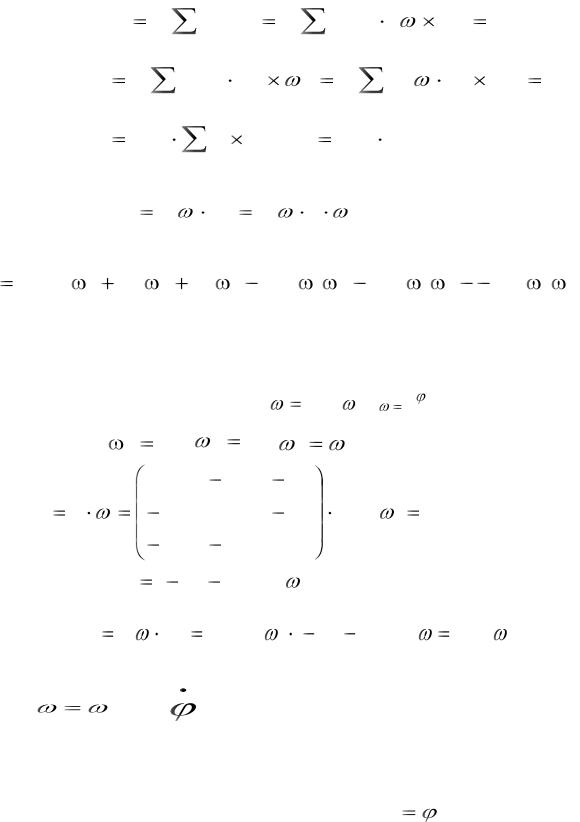
Формулы () свидетельствуют о том, что кинетический момент - вектор Go есть скалярное произведение тензора инерции тела на вектор угловой скорости:
Go I 

Кинетическая энергия абсолютно твердого тела с одной неподвижной точкой.
По определению кинетической энергии:
48
|
|
|
T |
1 |
|
|
|
m v |
2 |
|
|
|
1 |
|
|
|
|
m v |
|
( |
|
|
|
|
|
|
) |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
k |
|
|
|
r |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
k k |
|
|
|
|
2 |
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
k |
|
||||||||||||
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
mk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
mk |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
rk (vk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(rk |
vk ) |
||||||||||||||||||||||
|
|
|
2 |
|
|
k |
|
|
|
|
2 |
|
k |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
ω |
|
|
|
|
|
|
|
|
|
(m v |
|
|
) |
|
|
|
ω G |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
r |
k |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
k |
|
k |
|
|
|
|
|
2 |
|
|
|
|
|
o |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
T |
|
|
|
Go |
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Вычисления дают |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
2 |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
T |
|
( I xx x |
I yy |
|
y |
|
I zz z |
|
2I xy x |
|
|
|
y |
2I xz x z |
2I yz y z ) |
|||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Знание кинетической энергии тела позволяет составить уравнения движения твердого тела.
Вращение твердого тела вокруг неподвижной оси.
Ограничимся частным случаем, когда. у тела есть еще одна неподвижная точка,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
С осью вращения связываем ось О z. Тогда . |
(0,0, |
) |
, |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
dt |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
0 , |
y |
0 , |
|
z |
|
, |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
Ixx |
|
Ixy |
|
Ixz |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Go I |
|
|
|
|
|
|
Ixy |
I yy |
|
I yz |
(0,0, ) |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Ixz |
|
I yz |
Izz |
|
|
|
|
= |
|
|
|||
|
|
|
|
|
|
|
|
|
|
( Ixz , I yz , Izz ) |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
Т |
|
|
|
|
Go |
|
(0,0, |
) ( |
I xz , |
I yz , I zz ) |
|
|
I zz |
|||||||
|
|
|
|
2 |
|
2 |
2 |
|||||||||||||||||
(t ) 
Уравнение Лагранжа 2 рода для случая движения абсолютно твердого тела с двумя неподвижными точками.
Введем систему координат и обобщенную координату Q1 |
,которая определяет |
вращательную степень свободы. Оси ζ и z совпадают по построению. |
|

49
|
|
T |
|
|
1 |
I |
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||
|
2 |
z z |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Обобщенная координата одна qi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Уравнение Лагранжа 2 рода в рассматриваемом случае принимает вид: |
|
||||||||||||||||||||||||||||
|
|
d |
|
|
|
T |
|
|
|
|
|
|
|
|
T |
|
|
Q1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
dt |
|
|
q1 |
|
|
|
|
|
|
|
|
q1 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Обобщенная сила определяется коэффициентом, который стоит в выражении для |
|
|||||||||||||||||||||||||||
виртуальной работы, которая совершается на соответствующем возможном перемещении |
: |
||||||||||||||||||||||||||||
|
|
A |
M z |
|
|
|
|
|
Qi |
|
M z |
|
|
|
|
||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M z |
- сумма моментов относительно оси Oz всех сил, действующих на тело , |
|
|||||||||||||||||||||||||||
Q1 - обобщенная сила. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
T |
|
|
|
|
T |
0,i |
|
1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
qi |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
T |
|
|
|
|
|
|
T |
|
Izz |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
qi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
d |
( |
|
|
|
T |
) |
|
d |
(I |
|
) |
I |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
zz |
zz |
|
||||||||||||||||||
|
|
|
dt |
|
|
|
qi |
|
|
|
|
|
dt |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
то |
уравнение Лагранжа 2 рода для описания вращения движения тела вокруг неподвижной |
||||||||||||||||||||||||||||
оси имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
I zz |
|
M z |
|
|
|
|
|
|
|||||||||||||||
Если на тело не действуют силы, создающие момент относительно оси его вращения, или |
|
||||||||||||||||||||||||||||
моменты этих сил уравновешены, то M z |
0 . В этих случаях тело вращается по инерции, с |
|
|||||||||||||||||||||||||||
d
постоянной угловой скоростью const . Такое явление имеет место для планет и их dt
спутников.
Законы сохранения
1. Закон сохранения количества движения
|
n |
|
|
|
|
|
||||
Если |
|
F |
е 0 , то |
Q |
const , |
v const |
||||
|
|
k |
C |
|||||||
k1
2.Закон сохранения момента количества движения
n |
|
|
|
|
|
|
|
|
|
|
|
Если |
|
|
|
F |
е |
0 , то |
G const |
||||
r |
|||||||||||
|
|
k |
k |
|
|
O |
|||||
|
|
|
|
|
|
|
|
|
|
||
k |
1 |
|
|
|
|
|
|
|
|
|
|
3 Закон сохранения энергии
Интеграл энергии
Если внутренние и внешние силы потенциальные, то имеют место равенства
50
3 N |
Х е dх |
3 N |
U е |
|
dх |
|
dU е , |
3N |
Х i dх |
|
3 N |
U i |
dх |
|
dU i |
|
k |
хk , |
k |
|
k |
|
хk , |
k |
|||||||
|
k |
|
|
|
k |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
k 1 |
|
k 1 |
|
|
|
k 1 |
|
|
k 1 |
|
|
|
|||
Равенство () принимает вид |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
dT |
|
dU е U i ) |
|
|
|
|
|
|
|
|||
которое можно записать так
d(T U) 0
Следовательно, при движении механической системы в поле потенциальных сил, на нее действующих, выполняется закон сохранения полной механической энергии системы
T V const
Основная литература
1.Бухгольц Н.Н. Основной курс теоретической механики. М., т. 1 - 1965, 465 с., т. 11 -1966,
332 с.
2.2. Суслов Г.К. Теоретическая механика, М; Л. 1946, 655 с.
.
