
trubeckoy_c4
.pdf
Материал разработан преподавателем математики подготовительных курсов Учебного центра «Азъ» Трубецким Алексеем Петровичем
© Учебный центр «Азъ», 2012
Подготовка к С4
Треугольник, основные теоремы.
1.Две прямые пересекаются под углом 300 . От точки пересечения A на одной из прямых отложен
отрезок AB 1, на другой прямой отложен отрезок |
AC |
3 . Найти длину радиуса окружности, |
||||||||||||
|
|
|
Ответ: 1; |
|
|
|
|
|
|
|
|
C |
||
описанной около треугольника ABC . |
7 . |
|
|
|
||||||||||
|
|
|
|
|
||||||||||
I. Вариант. |
По теореме косинусов найдем |
|
|
|
|
|
|
A |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
BC AC2 |
AB2 2AC AB cos CAB 1. Радиус окружности |
|||||||||||||
|
|
|||||||||||||
найдем из теоремы синусов окружности R |
|
|
|
BC |
|
1. |
|
|
||||||
|
2sin 300 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
II. Вариант. |
Следует из чертежа. |
|
|
|
|
|
|
|
|
A |
B |
|||
|
|
|
|
|
|
|
|
C |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. На двух параллельных прямых, расстояние между которыми равно 12 , расположены вершины треугольника, боковые стороны которого равны 13. Найдите третью сторону треугольника.
Ответ: 10 ; 4 13 .
A
I. Вариант. |
Дано: AB AC 13 , AD 12 По теореме |
|
|
|
|||
|
|
|
|
|
|
|
|
Пифагора найдем DC |
AC2 AD2 |
5 . Сторона треугольника |
|
|
|||
BC 10 . |
|
|
|
|
|
|
|
|
|
|
|
B |
D C |
||
|
|
|
|
|
|||
A
II. Вариант. |
Пусть теперь треугольник расположен так, что |
|
|
|
|
|
B D |
C |
|||||
AB BC |
13. |
|||||
|
|
|
||||
3.В прямоугольном треугольнике ABC длины катет BC 4 равна AC 12 . На прямой AC взята
точка D так, что AD : DC 3 . Найдите sin ABD . |
Ответ: |
|
9 |
; |
|
9 |
. |
|
|
|
|
|
|
||||
|
5 |
10 |
|
130 |
|
|||
I. Вариант. По теореме Пифагора найдем AB 4
 10 . Найдем DC 3 , затем
10 . Найдем DC 3 , затем
DB 5 . Т.к. B , sin sin B cos cos B sin . Получаем
sin |
|
9 |
. |
|
|
|
|
||
5 |
10 |
|
||
Заметим, что можно было из треугольника ABD по теореме косинусов найти cos , затем sin .
A
D
C B
1

A
II. Вариант. Рассмотрите другой вариант положения точки D .
C B
D
4.Высоты треугольника ABC пересекаются в точке H . Известно, что CH AB . Найдите угол
ACB .
I. Вариант. |
Треугольники ABF и CHF равны, т.к. оба они |
прямоугольные, имеют по условию равные гипотенузы и |
|
угол FAB HCF как два острых угла со взаимно |
|
перпендикулярными сторонами. Следовательно, AF CF , и C |
|
треугольник AFC прямоугольный и равнобедренный, |
|
откуда ACB 450 . |
|
Рассмотрите вариант тупого угла C . Докажите равенство треугольников FAB и HCF , затем докажите, что FA CF .
Ответ: 450 ; 1350 .
A
E
H
B
F
A
E
B
F
C
H
5.В треугольнике ABC проведена прямая, параллельная AC и пересекающая стороны AB и BC в точках E и F соответственно. Прямая EF делит треугольник ABC на две фигуры, площади
которых относятся как 1: 3 . Найдите отношение длин отрезков AC и EF . |
|
Ответ: |
2 ; |
|
2 |
. |
||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
3 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
I. Вариант. |
Пусть SEBF : SAEFC 1:3 . Тогда |
|
|
|
|
|
B |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
SEBF : SABC 1: 4 . Треугольники ABC и EBF подобны, |
|
|
E |
|
|
M |
|
|
|
F |
||||||||||||||
причем коэффициент подобия k2 4 |
|
или k 2 . |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Следовательно, AC : EF 2 . |
|
|
|
|
A |
|
|
|
|
|
|
|
N |
|
|
C |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
II. Вариант. |
Рассмотрите случай SEBF : SAEFC 3:1. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
6. Площадь прямоугольного треугольника ABC C 900 равна 8 , длина катета |
BC равна 2 . |
|||||||||||||||||||||||
Прямая проходит через точку B и образует угол 450 с прямой BC . Найдите расстояние от точки |
||||||||||||||||||||||||
A до указанной прямой. |
|
Ответ: 3 |
|
|
; 5 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
I. Вариант. Из формулы площади следует, что AC 8 , по теореме |
A |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Пифагора найдем AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
68 . Найдем |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
sin sin 1350 |
sin1350 cos cos1350 sin , получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
||
|
5 |
2 |
. Затем AD AB sin 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
sin |
2 . |
|
|
C |
|
|
450 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
68 |
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2
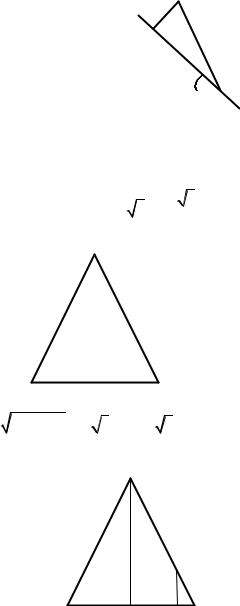
II. Вариант. Рассмотрите другой вариант положения точки прямой. |
|
|
|
|
|
|
|
D |
|
|
|
|
|
A |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
450 |
B |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|||||
7. В треугольнике ABC AB BC 13, а |
AC 10 . В треугольник вписан прямоугольник так, что две |
|||||||||||||||||||||||||
его вершины лежат на стороне AC , |
а две другие на сторонах AB и |
BC . Известно, что одна |
||||||||||||||||||||||||
сторона прямоугольника вдвое больше другой. Найдите диагональ прямоугольника. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
60 |
|
|
|
. |
|
|||
|
|
|
|
|
|
|
|
|
Ответ: 3,75 |
|
; |
5 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
5 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
17 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
I. Вариант. |
|
По теореме Пифагора найдем BD 12 . Из |
|
E |
|
|
B |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|||||||||||
треугольника BDC найдем tg C |
12 |
2,4 . Пусть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
MN x , |
тогда FN 2x , а NC 5 |
x |
. Из треугольника |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
A |
M |
D |
|
N |
|
|
|
C |
|
||||||||||||||||
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||
FCN следует, что FN CN tg C или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x2 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2x 5 |
|
2,4 . Получаем x 3,75 , Диагональ равна |
x |
5 3,75 |
5 . |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B
II.Вариант. Рассмотрите другой вариант расположения прямоугольника.
|
E |
|
F |
|
|
||
A |
|
M D N |
C |
3

Материал разработан преподавателем математики подготовительных курсов Учебного центра «Азъ» Трубецким Алексеем Петровичем
© Учебный центр «Азъ», 2012
Подготовка к С4
Окружность, основные теоремы.
1.Длина окружности равна 20 . Диаметр AB и хорда CD лежат на параллельных прямых.
Расстояние между указанными прямыми равно 
 19 . Найдите длину хорды BC . Ответ: 2
19 . Найдите длину хорды BC . Ответ: 2
 5 ; 2
5 ; 2
 95 .
95 .
I. Вариант. Длина окружности 20 2 R , откуда R 10 . Из
треугольника COK следует, что CK 
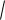 CO2 OK 2 9. Из треугольника COK находим cos OCK 0,9 . Далее
CO2 OK 2 9. Из треугольника COK находим cos OCK 0,9 . Далее
cos COA cos OCK 0,9 . По теореме косинусов находим
C |
K |
D |
A |
O |
B |
|
|
CA 2
 5 . Из прямоугольного треугольника ABC найдем
5 . Из прямоугольного треугольника ABC найдем
BC 2
 95 .
95 .
II.Вариант. Поменяйте местами точки C и D .
2.Площадь круга, ограниченного некоторой окружностью, равна 12 , AC – диаметр этой окружности, точка O – ее центр. Точка B лежит на окружности, причем площадь треугольника
AOB равна 3 . Найдите величину угла CAB . Ответ: 150 ; 750 .
|
|
|
|
|
B |
I. Вариант. |
Пусть AO R . Тогда R2 |
12 и R 12 . |
|
|
|
Треугольник AOB равнобедренный, его площадь |
|
|
|
||
|
|
A |
|
O |
C |
S 1 R2 sin , откуда sin 1 . При данном расположении |
|
|
|
||
2 |
2 |
1500 , откуда следует |
|
|
|
точки B угол тупой, следовательно, |
|
|
|
||
150 . |
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
O |
C |
II.Вариант. Рассмотрите вариант острого угла .
3.Площадь круга с центром в точке O равна 144 . Точки A и B расположены на расстоянии 12,5 и
26 соответственно от точки |
O . Длина хорды, лежащей на прямой AB равна 4 11 . Найдите |
площадь треугольника AOB . |
Ответ: 82,5 ; 157,5. |
I. Вариант. |
Длина R 12 . Из треугольника COK следует, что |
|
|
|
|
OK 10 . Из треугольника AOK находим AK 7,5 , а из |
|
O |
|
||
треугольника ABK находим BK 24 . Далее |
|
|
|
||
|
1 |
|
A |
D |
B |
SAOB |
|
AB OK 157,5 . |
C |
|
|
2 |
|
K |
|
||
|
|
|
|
|
|
|
|
|
|
|
1 |

II.Вариант. Рассмотрите случай, когда точки A и B лежат по одну сторону от хорды CD .
O
C D B K A
4. На окружности с радиусом R 3 последовательно поставлены точки K , M , |
N и P так, что |
||
дуги KM 400 и MN 1000 , а хорды KN и MP пересекаются под углом 700 . Найдите длину |
|||
наибольшей стороны четырехугольника KMNP . Ответ: 2 |
|
; 3 . |
|
3 |
|
||
|
|
K |
M |
I. Вариант. Сначала надо доказать, что наибольшей стороной является KP , для этого найдем величину дуги KP . Вписанный
угол KNM 200 , угол NOM 1100 , следовательно, угол
PNM 500 , а дуга PN 1000 . Дуга
KP 3600 1000 1000 400 1200 является наибольшей, следовательно хорда KP является также наибольшей. Треугольник
O
700
N
P
KNP вписан в
окружность и по теореме синусов KP 2R . Получаем KP 3 . sin KNP
K M
O 700
II.Вариант. Рассмотрите другой вариант расположения хорды
MP .
P
N
5. На стороне AB угла ABC 300 взята точка D такая, что AD 2 и |
BD 1. Найдите радиус |
|||
окружности, проходящей через точки A и D , и касающейся прямой BC . Ответ: 1; |
7 |
|||
|
|
E |
C |
|
|
|
|
||
I. Вариант. |
По теореме о касательной и секущей BE2 BA BD , |
B |
A |
|
откуда BE |
3 . По теореме косинусов найдем отрезки AE 3 |
|||
D |
|
|||
и DE 1. Треугольник ADE прямоугольный, следовательно, |
|
|
||
AD это диаметр и R 1. |
|
|
||
C
II.Вариант. Рассмотрите другой вариант расположения окружности относительно угла ABC .
B D
A
E
2

Материал разработан преподавателем математики подготовительных курсов Учебного центра «Азъ» Трубецким Алексеем Петровичем
© Учебный центр «Азъ», 2012
Подготовка к С4
Вписанные и описанные окружности
1.В треугольник ABC вписана окружность. Точка касания окружности стороны AС делит ее на
отрезки с длинами 6 и 4 . Периметр треугольника равен 24 . Найдите sin BAC . Ответ:0,6 ; 0,8 .
I. Вариант. Пусть CK CM 6 , AK AL 4 , а
BL BM x . Тогда 2 4 2 6 2x 24 и x 2 . Длины сторон треугольника таковы, что он является прямоугольным с
гипотенузой AC . Получаем sin BAC BC 0,8 .
AC
II. Вариант. Пусть CK CM 4 , AK AL 6 .
C
K
M
B A L
2. Треугольник |
ABC вписан в окружность радиуса 12 . Известно, что AB 6 и BC 4 . |
Найдите |
||||
AC . |
Ответ: |
35 |
|
|
15 |
. |
I. Вариант. |
Из теоремы синусов следует, что Пусть |
|
||
BC |
2R , |
откуда sin A 1 . Аналогично найдем |
C |
|
sin A |
|
6 |
|
|
|
|
|
||
sin C 1 . Очевидно, что A острый, BL BM x . Тогда |
|
|||
|
4 |
|
|
|
cos A 35 |
|
A |
||
|
B |
|||
. Угол C может быть и острым, и тупым. |
|
|||
|
6 |
|
|
|
Рассмотрим вариант острого угла, тогда cos C |
15 . Найдем |
|
||
|
|
|
4 |
|
sin sin Acos C cos Asin C , т.е. sin |
35 15 . По теореме синусов найдем |
|||
|
|
|
24 |
|
AC |
35 |
15 . |
|
|
1

II. Вариант. Пусть C тупой, тогда cos C 15 . 4
A |
B |
C
3.Угол между радиусом AO окружности, описанной около треугольника ABC и стороной AC
равен 450 . Найдите угол A треугольника ABC , если угол C равен 250 . |
Ответ: 1100 ; 200 . |
I. Вариант. |
Проведем радиус OC . Треугольник AOC |
B |
O |
|
равнобедренный, следовательно, O 900 , а B 450 . Получаем |
|
450 |
||
A 1800 |
250 450 1100 . |
A |
||
C |
||||
II. Вариант. |
Рассчитайте самостоятельно. |
O |
|
||
|
A |
450 |
|
C |
|
|
|
B |
4.Около треугольника ABC описана окружность с центром O , угол AOC 600 . В треугольник
ABC вписана окружность с центром M . Найдите угол AMC . |
Ответ: 1650 ; 1050 . |
C
I. Вариант. |
0 |
M лежит |
|
|
Пусть B острый, тогда B 30 . Точка |
|
|
||
на пересечении биссектрис, значит, 2 2 1800 300 |
1500 , |
O |
M |
|
откуда 750 . Далее AMC 1800 1050 |
. |
|
|
|
B |
A |
|||
|
|
|
|
|
C
II. Вариант. Пусть B тупой, тогда B 3600 600 1500 .
2
O
B
A
2

5.Прямая отсекает от сторон прямого угла отрезки с длинами 3 и 4 . Найдите радиус окружности,
касающейся этой прямой и сторон угла |
Ответ: 1; 6 . |
I. Вариант. Пусть CB 4 и AC 3 , тогда AB 5 . Обозначим BE BF x и AF AD y . Тогда x y 5 и x 4 y 3, т.к. CDOE квадрат. Находим x 2 , R x 4 6 .
D |
|
O |
|
|
|
A |
|
|
|
F |
|
C |
B |
E |
II.Вариант. Совсем простой, т.к. получается окружность, вписанная в египетский треугольник.
6. В треугольнике ABC AB BC 10, AC 12 . В треугольник вписана окружность. Касательная к этой окружности, параллельная высоте BD , пересекает стороны треугольника в точках F и E .
Найдите длину радиуса окружности, описанной около треугольника CFE . Ответ: 2,5, 0,5
 97
97
I. Вариант. Найдем BD 
 100 36 8 . Площадь
100 36 8 . Площадь
SABC 48, полупериметр |
p 16 .. Тогда r |
S |
3 и |
|
|||
|
|
p |
|
OD DF r 3. Тогда FC DC DF 3.
Треугольник DBC подобен треугольнику FEC с коэффициентом подобия k 2 . Следовательно, треугольник FEC – египетский, и длина искомого
радиуса R EC 2,5 . 2
II.Вариант. Рассчитайте второй вариант согласно чертежу.
|
B |
E |
|
|
|
|
O |
|
A |
D |
C |
|
F |
B
E
O
C
A
F D
7.Площадь квадрата ABCD равна 16 . Окружность проходит через вершину A и касается прямых
BC и CD . Найдите радиус этой окружности. |
Ответ: 4 |
2 |
|
2 |
1 ; 4 |
2 |
|
2 |
1 . |
I. Вариант. Сторона квадрата равна 4 . Диагональ AC 4
 2 . Пусть OF OE R . Тогда
2 . Пусть OF OE R . Тогда
AC AO OC R R
 2 . Отсюда
2 . Отсюда
|
4 |
2 |
|
|
|
|
|
|
|
R |
|
4 2 |
2 1 . |
||||||
|
|
1 |
|||||||
|
2 |
||||||||
B |
E |
|
C |
||
|
||
O |
F |
|
A |
D |
|
|
3

II. Вариант. |
Рассчитайте второй вариант согласно |
E |
B |
C |
чертежу. |
|
|
A |
D |
|
|
|
||
|
|
|
|
|
|
|
O |
|
F |
|
|
|
|
4
Материал разработан преподавателем математики подготовительных курсов Учебного центра «Азъ» Трубецким Алексеем Петровичем
© Учебный центр «Азъ», 2012
Подготовка к С4
Четырехугольники.
1. В параллелограмме ABCD AB 4 , |
BC 2 |
. Площадь параллелограмма равна 4 3 . Круг с |
||||
центром в точке A касается прямой BD . |
Найдите площадь части круга, расположенной |
|||||
внутри параллелограмма. |
|
Ответ: |
2 |
; |
4 |
. |
|
|
7 |
||||
|
|
3 |
|
|
||
I. Вариант. |
Площадь параллелограмма S AD AC sin A , откуда sin A |
3 |
. |
|
2
По чертежу A острый, следовательно, A 600 и cos A 0,5 . В треугольнике ABD по теореме
косинусов найдем BD 2 3 . Проведем в точку |
||||
касания радиус AK , который является высотой |
||||
треугольника ABD . Площадь SABD |
1 |
BD AK , |
||
|
|
|||
2 |
|
|||
откуда AK 2 . Площадь круга AK 2 |
4 . |
|||
Внутри параллелограмма находится |
1 |
|
часть круга. |
|
|
||||
6 |
|
|
||
II. Вариант. Рассчитайте вариант тупого A .
K
B C
A D
B C
K
A D
2. В параллелограмме ABCD биссектрисы при стороне AD делят сторону BC в точках M и N так, что BM : MN 1: 5 . Найдите длину стороны BC , если AB 3 . Ответ: 3,5 ; 21.
I. Вариант. |
Треугольник ABN равнобедренный, |
B |
M |
|
N |
C |
следовательно, BN 3 , и BM 0,5 . Треугольник |
|
|
|
|
|
|
DMC также равнобедренный и CM 3 . |
|
|
|
|
|
|
|
|
|
|
|
||
Получаем BC BM MC 3,5 . |
A |
|
|
D |
|
|
1
