
Графики
.pdf
не дифференцируема в точке минимума a = 0). Таким образом, точки локального экстремума функции f следует искать среди так называемых критических точек.
Определение 10. Пусть a внутренняя точка области определения D(f) функции f. Точка a называется критической точкой функции f, если либо f дифференцируема в точке a и f0(a) = 0, либо f не дифференцируема в точке a. Точки, в которых f0(a) = 0, называются стационарными точками функции f.
Теорема 4. Пусть a критическая точка функции f; f дифференцируема в некоторой ее окрестности (a ; a + ), кроме, возможно, самой точки a. Если производная f0(x) меняет знак при переходе через точку a, то есть на интервалах (a ; a) и (a; a + ) f0(x) имеет противоположные знаки, то a точка экстремума функции f. При этом, если
f0(x) > 0 на (a ; a) и f0(x) < 0 на (a; a + );
то a является точкой максимума функции f, а если
f0(x) < 0 на (a ; a) и f0(x) > 0 на (a; a + );
то a является точкой минимума функции. Если же f0(x) не меняет знак при переходе через a, то a не является точкой экстремума функции f.
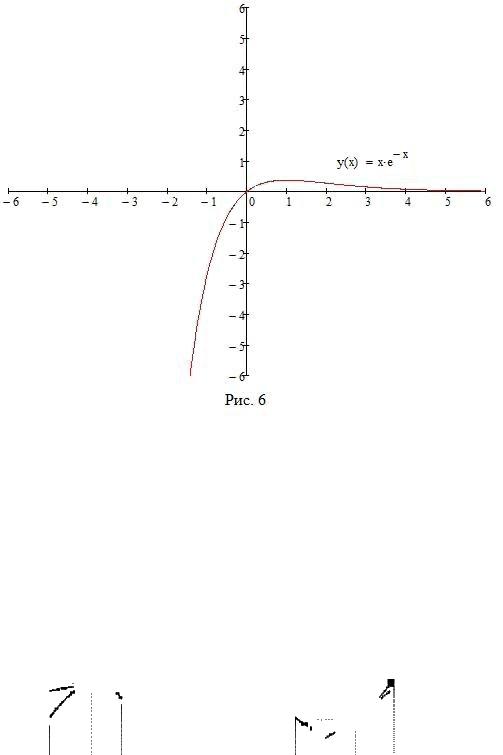
Пример 4. Исследовать на экстремумы, указать промежутки монотонности функции f(x) = xe x.
Решение. Функция f дифференцируема на R, поскольку x и e x дифференцируемы на R. Значит, множество критических точек совпадает с множеством стационарных. Найдем стационарные точки. Так как f0(x) = e x(1 x), x 2 R, то единственной стационарной точкой является a = 1. Определяем знаки f0 :
sgn f0(x) |
+ |
1r |
|
- |
f(x) |
|
Qs |
|
|
|
3 |
|
Q |
|
Следовательно, f возрастает на (1; 1]; убывает на [1; +1); a = 1 точка локального максимума функции f: Значение f(1) = e 1 = 1e экстремальное значение функции f (см. Рис. 6) : 

11
1.5 Направления выпуклости графика функции. Точки перегиба
Определение 11. Пусть функция f дифференцируема на интервале (a; b): Говорят, что на этом интервале график f функции f обращен выпуклостью вверх (соответственно, вниз), если он лежит на нем не выше (не ниже) касательных, проведенных к f в точках (x; f(x)), x 2 (a; b).
Виды графиков выпуклых вверх и выпуклых вниз функций приведены соответственно на Рис. 7 и 8.
|
|
y |
6 |
|
|
|
|
|
|
|
|
|
y |
6 |
|
|
|
|
|
|
|
|
|
|
||||
f(x) |
|
|
|
|
|
|
- |
|
|
|
|
|
f(x) |
|
|
|
|
|
|
|
- |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
a 0 |
|
x b |
x |
a 0 |
|
|
|
x b |
x |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
Рис. 7 |
|
|
|
|
|
|
Рис. 8 |
|
|
||||||||||||||||
Направления выпуклости определяются по второй производной функции f.
Теорема 5 (достаточное условие направления выпуклости). Пусть функция f дважды дифференцируема на интервале (a; b): Если f00(x) 0 (f00(x) 0)
12

на |
(a; b), то график f обращен выпуклостью вверх (соответственно вниз) |
на |
(a; b). |
Перейдем к точкам перегиба.
Определение 12. Пусть функция f определена в некоторой окрестности (a ; a + ) точки a, дифференцируема на (a ; a + ) n fag и непрерывна в точке a. Если на интервалах (a ; a) и (a; a + ) график f имеет разные направления выпуклости, то a называется точкой перегиба функции f. Точка (a; f(a)) называется точкой перегиба графика f .
Как известно, если a точка перегиба функции f и f дважды дифференцируема в точке a, то f00(a) = 0. Однако, функция может и не быть дважды
5
дифференцируемой в точке перегиба. Например, f(x) = x3 определена и дифференцируема на R, дважды дифференцируема на R n f0g, f00(x) = 109 x 13 , x 6= 0. Следовательно, на интервале (0; +1) ее график обращен выпуклостью вниз, а на интервале ( 1; 0) выпуклостью вверх. Значит, рассматриваемая функция имеет перегиб в точке a = 0.
Таким образом, к точкам возможного перегиба следует отнести те внутренние точки a 2 D(f); в которых f непрерывна и либо f дважды дифференцируема и f00(a) = 0; либо f не является дважды дифференцируемой в этой точке.
Достаточное условие перегиба формулируется следующим образом.
Теорема 6 (достаточное условие перегиба). Пусть a точка возможного перегиба функции f; f дважды дифференцируема в некоторой окрестности точки a, кроме, возможно, самой точки a. Если f00(x) по разные стороны от точки a имеет разные знаки, то a точка перегиба функции f. Если же знаки f00(x) слева и справа от точки a одинаковы, то a не является точкой перегиба функции f.
Пример 5. Исследовать на перегибы, указать направления выпуклости графика функции f(x) = x3:
Решение. Функция f(x) = x3 дважды дифференцируема на R и f00(x) = 6x при всех x 2 R: Следовательно, x = 0 единственная возможная точка перегиба функции f. Определяем знаки f00 на интервалах ( 1; 0) и (0; +1).
sgn f00(x) |
|
0r |
+ |
|
- |
||
f(x) |
|
13
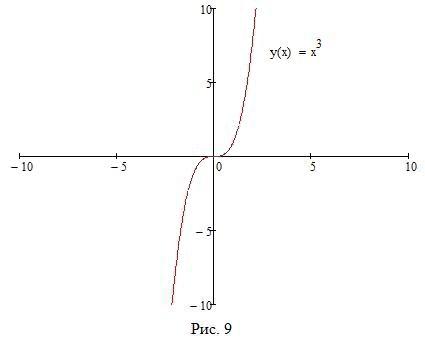
Значит, на (1; 0) график f обращен выпуклостью вверх, а на (0; +1) выпуклостью вниз, a = 0 точка перегиба функции f (см. Рис. 9). 
2 Задачи с решениями
Пример 6. Исследовать функцию f(x) = x 2arctg x и построить эскиз ее графика.
Решение. 1) Область определения D(f) = R (множество симметрично относительно 0). Так как
f( x) = x 2arctg ( x) = x + 2arctg x = f(x); x 2 R;
то функция f является нечетной. Понятно, что f не является периодической. Найдем точки пересечения f с осями координат. Если x = 0; то f(x) = 0:
Значит, f пересекает ось Oy в начале координат (0; 0). Точки пересечения с осью Ox определяются из уравнения f(x) = 0 , x 2arctg x = 0. Как будет видно из последующего, данное уравнение, кроме нулевого решения, имеет еще
идва ненулевых, которые можно найти лишь приближенно.
2)Функция f непрерывна на R как разность элементарных непрерывных функций x и 2arctg x. Из этого следует, что вертикальных асимптот у f нет
3)Проведем исследование на наличие наклонной асимптоты при x ! +1:
14

Так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
lim |
f(x) |
|
lim |
1 |
|
2arctg x |
|
= 1 =: k; |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||||||||
x!+1 |
|
|
x = x!+1 |
|
|
|
|
|
|
|
|
|
||||||||||
x + |
(f(x) |
|
kx) = |
x + |
|
(x |
|
2arctg x |
x) = |
x + |
( |
|||||||||||
lim |
|
lim |
|
|
|
lim |
|
2arctg x) = =: b; |
||||||||||||||
! 1 |
|
|
|
|
|
|
|
! 1 |
|
|
|
|
|
|
|
! 1 |
|
|
|
|||
то прямая y = x является наклонной асимптотой f |
при x ! +1. Анало- |
|||||||||||||||||||||
гично, поскольку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
lim |
|
f(x) |
= lim |
1 |
|
2arctg x |
= 1 =: k; |
|
|
|
|
|||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
||||||||||
x! 1 x |
|
x! 1 |
|
|
|
|
|
|
|
|
|
|
( 2arctg x) = =: b; |
|||||||||
xlim |
|
(f(x) kx) = xlim |
(x 2arctg x x) = xlim |
|
||||||||||||||||||
! 1 |
|
|
|
! 1 |
|
|
|
|
|
|
! 1 |
|
|
|||||||||
прямая y = x + является наклонной асимптотой f |
при x ! 1. |
|||||||||||||||||||||
4) Функция f дифференцируема на R, так что множество критических точек совпадает с множеством стационарных. Найдем стационарные точки. Имеем:
f0(x) = 1 |
|
2 |
= |
x2 1 |
; x |
2 R |
: |
|
1 + x2 |
1 + x2 |
|||||||
|
|
|
|
Значит, 1 стационарные точки функции f. Определяем знаки f0 на трех образовавшихся интервалах.
sgn f0(x) |
+ |
|
+ |
|
|
- |
|
f(x) |
-1r |
Qs1r |
|
|
3 |
Q |
3 |
Следовательно, f возрастает на (1; 1] и на [1; +1), убывает на [ 1; 1], x = 1 точка локального максимума функции f, x = 1 точка локального минимума функции f. Экстремальные значения функции f :
f( 1) = 1 + |
|
; |
f(1) = 1 |
|
: |
|
|
||||
2 |
2 |
5) Проведем исследование на направление выпуклости и перегиб. Функция
f дважды дифференцируема на R и |
|
|
|
|
f00(x) = |
4x |
|
|
; x 2 R: |
|
|
|||
(1 + x2)2 |
||||
sgn f00(x) |
|
0r |
+ |
|
|
- |
|||
f(x) |
|
|||
15
Решая уравнение f00(x) = 0, получим, что x = 0 точка возможного перегиба функции f: Определяем знаки f00:
Значит, на интервале ( 1; 0) график обращен выпуклостью вверх, а на (0; +1) выпуклостью вниз; x = 0 точка перегиба функции f.
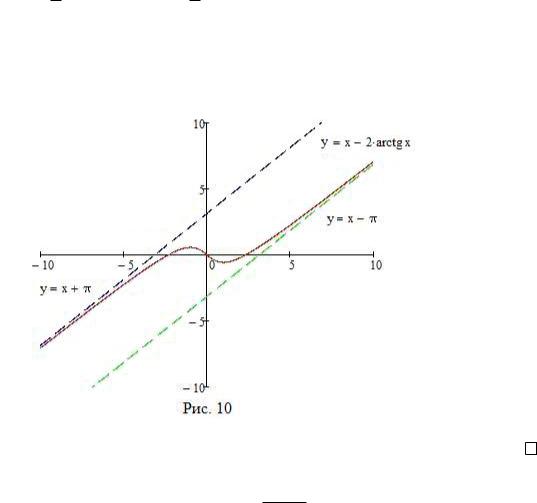
6) Переходим к построению эскиза f , который должен получиться симметричным относительно (0; 0): Наносим точки, через которые проходит график: (0; 0) точка пересечения с осью Oy; которая одновременно является точкой перегиба f , 1; 1 2 и 1; 1 + 2 точки локального минимума и максимума соответственно. Пунктиром строим наклонные асимптоты f . Далее, учитывая характер монотонности и направления выпуклости, рисуем графикf функции f (cм. Рис. 10).
x3
Пример 7. Исследовать функцию f(x) = x 1 и построить эскиз ее графика.
Решение. 1) Данная функция является дробно-рациональной. Ее область определения D(f) = R n f1g несимметрична относительно 0, так что f не может быть ни четной, ни нечетной. Функция f не является периодической. Так как f(x) = 0 , x = 0, то f пересекает оси координат в единственной точке (0; 0):
2) Функция f непрерывна на своей области определения Rnf1g. Точка a = 1 не принадлежит D(f), но является двусторонней предельной точкой D(f), по-
16
этому a = 1 точка разрыва функции f. Установим ее род. Так как
x 1 0 |
x 1 0 x |
x3 |
1 |
1 |
|
||
lim f(x) = |
lim |
|
|
|
= |
|
; |
! |
! |
|
|
|
|
||
то a = 1 точка разрыва 2-го рода. Одновременно из этого вытекает, что прямая x = 1 является двусторонней вертикальной асимптотой графика f .
3) Поскольку |
|
|
|
|
|
|
|
|
|
|
|
xlim |
f(x) |
= xlim |
|
x2 |
|
|
= xlim |
|
x |
= 1; |
|
|
|
|
|
|
|
|
|
||||
x |
|
x |
|
1 |
|
1 |
|||||
! 1 |
|
|
! 1 |
|
|
|
! 1 1 |
x |
|
||
наклонных асимптот f не имеет.
4) Функция f дифференцируема на D(f), следовательно, множество ее критических точек совпадает с множеством стационарных. Имеем:
f0(x) = |
3x2(x 1) x3 |
= |
x2(2x 3) |
; x |
1 : |
|
(x 1)2 |
(x 1)2 |
|||||
|
|
|
2 R n f g |
Значит, 0 и 32 стационарные точки функции f. Определяем знаки f0 на четырех образовавшихся интервалах.
|
|
|
sgn f0(x) |
|
|
|
|
|
|
2r |
+ |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
||||||||
|
|
|
f(x) |
|
sQ 0r sQ 1b |
sQ |
|
|
|
|
|
||||||||||
|
|
|
|
Q |
|
Q |
|
Q |
3 |
|
3 |
|
|
|
|
||||||
3 |
|
h |
3 |
3 |
|
|
27 |
|
|
|
3 |
i |
|||||||||
Следовательно, f возрастает на |
|
|
2 |
; +1 |
, убывает на (1; 1) и на |
1; |
2 |
; |
|||||||||||||
x = |
|
точка локального минимума, f |
|
|
= |
|
. |
|
|
|
|
|
|
||||||||
2 |
2 |
4 |
|
|
|
|
|
|
|||||||||||||
5) Функция f дважды дифференцируема на D(f) и при всех x 2 D(f) |
|
|
|
||||||||||||||||||
|
f00(x) = |
(6x2 6x)(x 1)2 (2x3 3x2) 2(x 1) |
= |
2x(x2 3x + 3) |
: |
|
|
||||||||||||||
|
|
|
(x 1)4 |
|
|
|
|
|
|
|
|
|
(x 1)3 |
|
|
|
|||||
|
|
|
sgn f00(x) |
|
|
|
+ |
|
|
|
+ |
|
|
|
|
|
|
|
|
||
|
|
|
f(x) |
|
|
|
|
0r |
|
1b |
|
|
- |
|
|
|
|
|
|
||
Решая уравнение f00(x) = 0, получим, что x = 0 точка возможного перегиба функции f. Заметим, что квадратный трехчлен x2 3x + 3 принимает только положительные значения. Определяем знаки f00: Значит, на интервалах
17
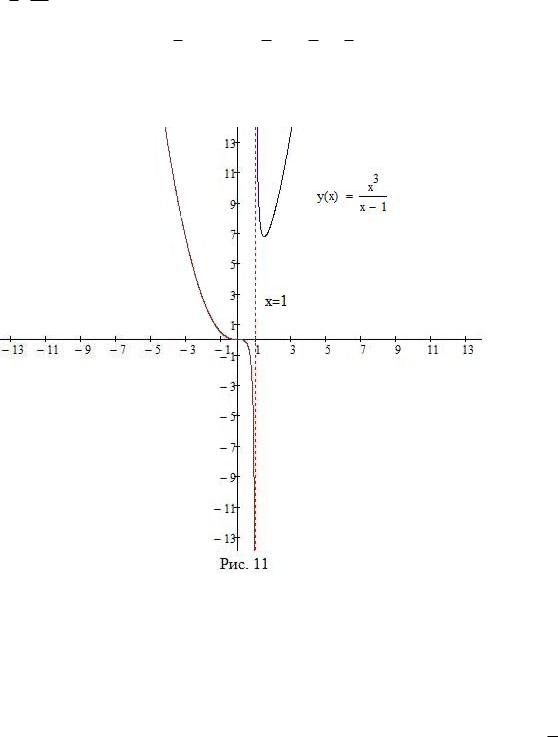
( 1; 0) и (1; +1) f обращен выпуклостью вниз, а на (0; 1) выпуклостью вверх; x = 0 точка перегиба функции f.
6) Переходим к построению эскиза f . Наносим точки, через которые проходит график: (0; 0) точка пересечения с осями координат и одновременно точка
перегиба, 32; 274 точка локального минимума. Возьмем для построения еще
вспомогательные точки: 2; 83 , 1; 12 , 12; 14 , (2; 8). Пунктиром строим вертикальную асимптоту x = 1. Далее, учитывая характер монотонности и направления выпуклости, рисуем график функции f (см. Рис. 11). 
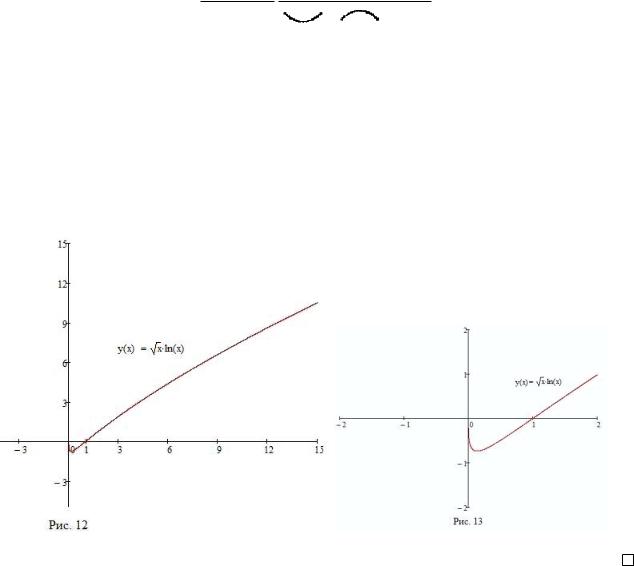
Пример 8. Исследовать функцию f(x) = |
p |
|
ln x и построить эскиз ее |
x |
|||
графика. |
|
|
|
Решение. 1) Область определения D(f) = (0; +1). Функция f не является ни четной, ни нечетной, ни периодической. Поскольку f(x) = 0 , x = 1, график
пересекает ось Ox в единственной точке (1; 0):
p
2) Функция f непрерывна на (0; +1); так как элементарные функции x и ln x непрерывны на (0; +1). Из этого следует, что f не имеет точек разрыва.
18

Точка 0 правосторонняя предельная точка D(f); так что f |
может иметь в |
|||||||||||||
ней вертикальную асимптоту. Используя правило Лопиталя, получим: |
||||||||||||||
|
lim p |
|
|
|
ln x |
|
|
1 |
|
|
2p |
|
|
|
|
|
ln x = |
lim |
= |
|
x |
|
|
|
|
||||
lim f(x) = |
x |
lim |
= lim |
x |
= 0: |
|||||||||
|
|
|||||||||||||
x!+0 |
x!+0 |
x!+0 x 21 |
x!+0 21x 23 |
x!+0 |
|
|
|
|||||||
Следовательно, прямая x = 0 не является вертикальной асимптотой f .
3) Проведем исследование на наличие наклонной асимптоты при x ! +1:
Так как |
|
f(x) |
|
|
|
ln x |
|
|
|
|
|
|
|||
|
lim |
|
lim |
= 0 =: k; |
|
|
|||||||||
|
x |
|
|
|
|
|
|
||||||||
x!+1 |
= x!+1 px |
|
|
|
|
|
|||||||||
x + |
|
|
|
|
x |
+ |
|
|
|
1 |
|
||||
|
lim (f(x) |
|
kx) = |
lim |
px ln x = + |
|
; |
||||||||
|
! 1 |
|
|
|
|
|
! 1 |
|
|
|
|
|
|||
то f не имеет наклонной асимптоты при x ! +1.
4) Функция f дифференцируема на (0; +1), так что множество критических точек совпадает с множеством стационарных. Найдем стационарные точ-
ки. Имеем, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f0 |
|
|
1 |
|
|
|
|
p |
|
|
1 |
|
ln x + 2 |
|
|
|
|
||||
x |
|
|
|
x |
|
x |
|
; x |
|
; |
: |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
( |
) = |
2px ln |
|
+ |
|
|
|
x |
= 2px |
|
2 |
(0 +1) |
|
|||||||
Решая уравнение f0(x) = 0; получим, что e12 стационарная точка функции f. Определяем знаки f0 на двух образовавшихся интервалах.
|
|
sgn f0(x) |
|
|
0b |
|
|
e2r |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
f(x) |
|
|
sQ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
Q |
|
|
1 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|||||||
Следовательно, f |
возрастает на |
|
|
; +1 |
|
|
, убывает на |
|
0; |
|
; x = |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
e2 |
|
|
e2 |
|
e2 |
||||||||||||||||||||
точка локального минимума |
функции f. Экстремальное значение функции f: |
|||||||||||||||||||||||||
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
||||||||
|
|
|
|
f |
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
= |
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
e2 |
e |
|
|
|
|
|
|
|
|
|
|
|||||||||||
5) Функция f дважды дифференцируема на (0; +1) и |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
x1 2p |
|
(ln x + 2) x 21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
f00(x) = |
x |
= |
|
ln x |
; |
x |
2 |
(0; + |
1 |
): |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
4x |
|
|
|
|
|
|
|
|
|
4x2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
Решая уравнение f00(x) = 0, получим, что x = 1 точка возможного перегиба функции f. Определяем знаки f00:
19
sgn f00(x) |
|
+ |
|
f(x) |
0b |
1r |
- |
Значит, на интервале (0; 1) график обращен выпуклостью вниз, а на (1; +1) выпуклостью вверх; x = 1 точка перегиба функции f.
6) Переходим к построению эскиза f . Наносим точки, через которые про-
ходит график: (1; 0) точка пересечения с осью Ox, |
|
1 |
2 |
точка ло- |
||
|
|
; |
|
|||
|
e2 |
e |
||||
кального минимума. Далее, учитывая характер |
монотонности и направления |
|||||
|
|
|
|
|
|
|
выпуклости, рисуем график f функции f (см. Рис. 12 и 13).
3 Построение параметрически заданных кривых
Напомним сначала основные сведения о параметрически заданных функциях.
Определение 13. Пусть T; X; Y некоторые множества в R: Если даны две функции x = x(t) : T ! X, y = y(t) : T ! Y; причем x(t) биективна, то можно определить суперпозицию y x 1, которая действует из X в Y и называется параметрически заданной функцией. Параметрически заданная функция обычно записывается в виде
y = y(x) : |
y = y(t) ; t 2 T: |
|
x = x(t) |
20
