Графики

При этом t параметр, T область изменения параметра, X = x (T ) область определения параметрически заданной функции.

Обычно рассматривается случай, когда T некоторый промежуток в R, x0(t) 6= 0 при всех t 2 T: Данное условие автоматически влечет, что либо x0(t) > 0 для любых t 2 T , либо x0(t) < 0 для любых t 2 T , так что функция x(t) будет строго монотонной на T и, значит, будет взаимно однозначно отображать T на образ X = x (T ). Множество X легко находится. Именно, если, например, T = ( ; ) и x(t) возрастает на ( ; ), то

0, t 2 T: Тогда, как известно, параметрически заданная функция y = y(x) дифференцируема на X и ее производная также является параметрически заданной функцией

8

< x = x(t)

y0(t) ; t 2 T: : y = x0(t)

Соответственно, промежутки возрастания и убывания рассматриваемой пара-

y0(t)

метрически заданной функции y = y(x) определяются знаком дроби x0(t).

Если x(t) и y(t) дважды дифференцируемы на промежутке T , то существует

Например, параметрическое уравнение окружности с центром (0; 0) радиуса R выглядит следующим образом:

21

Если ни одна из функций x(t); y(t) не является инъективной на T , то соотношения (1) не могут определять ни параметрически заданную функцию y = y(x), ни параметрически заданную функцию x = x(y). Однако, как правило, промежуток T можно разбить на конечное число промежутков монотонности функции x(t). Тогда на каждом из них (1) описывают свою параметрически заданную функцию y = y(x); которую называют ветвью рассматриваемой параметрически заданной кривой.

Для того чтобы построить параметрически заданную кривую, нужно сделать следующее:

1.Определить, являются ли функции x(t); y(t) четными или нечетными, сделать вывод о возможной симметрии кривой. Найти точки пересечения кривой с осями координат Oy и Ox, решив соответствующие уравнения x(t) = 0

и y(t) = 0.

2.Указать горизонтальные и вертикальные асимптоты кривой, а также найти наклонные асимптоты, если они есть.

3.Вычислить производные x0t и yt0; найти критические точки для x(t) и y(t), определить знаки x0t и yt0 на образовавшихся интервалах. Выделить ветви кривой.

4.Нанести на числовую ось все критические точки функций x(t) и y(t), разбив множество T на конечное число промежутков. Заполнить таблицу, внося в нее сведения о монотонности x(t) и y(t) на каждом из промежутков и делая вывод о поведении самой кривой при данных значениях t.

5.Вычислить вторую производную yxx00 , приравнять ее к 0 и найти значения параметра t, при которых на кривой возможны точки перегиба. На образовавшихся промежутках определить знаки yxx00 и сделать вывод о направлении выпуклости.

6.Выяснить, есть ли у кривой точки самопересечения. Для этого решить си-

стему

22

7. Построить эскиз параметрически заданной кривой.

Приведем некоторые пояснения по пунктам сформулированного алгоритма.

3.1 Симметрия

Пусть множество T симметрично относительно 0: Легко понять, что

если x(t) четная функция, а y(t) нечетная функция, то кривая бу-

дет симметрична относительно оси Ox, поскольку если при t0 > 0 кривой принадлежит точка (x0; y0), то при t0 получим точку (x0; y0);

если x(t) нечетная функция, а y(t) четная, то кривая симметрична относительно оси Oy;

если x(t) и y(t) нечетные функции, то кривая будет симметрична относительно начала координат.

3.2Асимптоты параметрически заданной кривой

Теорема 7. Пусть t0 2 R [ f 1g предельная точка T . Если одновременно выполняются равенства

то прямая x = a является вертикальной асимптотой рассматриваемой параметрически заданной кривой.

Теорема 8. Пусть t0 2 R [ f 1g предельная точка T . Если одновременно выполняются равенства

то прямая y = b является горизонтальной асимптотой рассматриваемой параметрически заданной кривой.

Наклонные асимптоты параметрически заданная кривая может иметь при тех значениях t0 2 R[ f 1g ; t0 предельная точка T , для которых одновременно

23

Из критерия наклонной асимптоты функции одной переменной легко вытекает следующая теорема.

Теорема 9. Пусть t0 значение параметра, при котором у кривой возможна наклонная асимптота. Для определенности пусть, например,

lim x(t) = lim y(t) = 1 :

t!t0+0 t!t0+0

Для того чтобы прямая y = kx + b, k 6= 0; была наклонной асимптотой рассматриваемой параметрически заданной кривой, необходимо и достаточно, чтобы

lim y(t) = k;

t!t0+0 x(t)

lim y(t)) kx(t) = b:

t!t0+0

3.3 Ветви параметрически заданной кривой

Количество ветвей кривой соответствует количеству промежутков монотонности функции x(t).

3.4Монотонность функций x(t); y(t) и поведение кривой

Вследующей таблице приведены четыре возможных варианта поведения кривой.

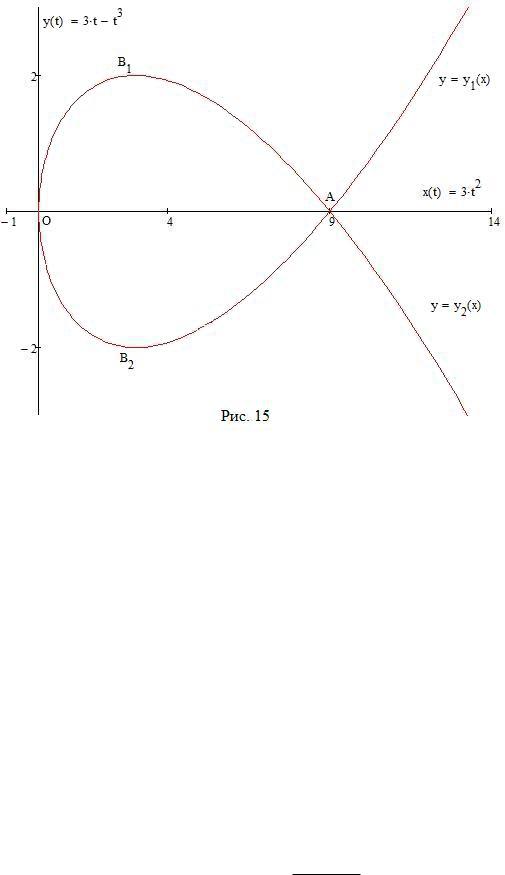
Пример 9. Построить параметрически заданную кривую

x = 3t2; y = 3t t3 :

Решение. 1) Естественной областью изменения параметра t является множество R. Так как x(t) четная функция, а y(t) нечетная функция, то кривая симметрична относительно оси Ox. Соответственно, достаточно построить часть кривой при t 2 [0; +1).

Найдем точки пересечения с осями координат.

24

С Oy : x(t) = 0 , t = 0: При t = 0 имеем точку O(0; 0):

С Ox : y(t) = 0 , 3t t3 = 0 , t = 0 p : t = 3

p

При t = 0 получаем ту же точку O(0; 0), а при t = 3 точку A(9; 0).

2) Бесконечные пределы функции x(t); y(t) имеют только при t ! 1 и

Это говорит о том, что вертикальных и горизонтальных асимптот у кривой нет. Выясним вопрос о наличии наклонных асимптот. Поскольку

3) Имеем, что x0(t) = 6t, y0(t) = 3 3t2 при всех t 2 R; так что x0(t) = 0 , t = 0;

y0(t) = 0 , t = 1:

На образовавшихся промежутках функции x0(t) и y0(t) имеют следующие знаки:

При t = 0 и t = 1 на кривой получаем точки O(0; 0) и B1;2(3; 2). У функции x(t) два промежутка монотонности, так что у кривой две ветви:

4) Заполним таблицу, чтобы понять поведение кривой на полученных промежутках изменения параметра.

25

Значит, yxx00 > 0 при t 2 (1; 0) и yxx00 < 0 при t 2 (0; +1). Таким образом, первая ветвь кривой обращена выпуклостью вниз, а вторая выпуклостью

A точка самопересечения кривой.

7) Переходим к построению эскиза параметрически заданной кривой. Наносим точки, через которые проходит график: O(0; 0), A(9; 0) B1;2(3; 2). Далее, учитывая характер монотонности и направление выпуклости, рисуем параметрически заданную кривую (см. Рис. 15).

Пример 10. Построить параметрически заданную кривую

Решение. 1) Естественной областью изменения параметра t является множество R n f1g. Функции x(t) и y(t) ни четные, ни нечетные.

Найдем точки пересечения с осями координат.

С Oy : x(t) = 0 , t = 0: При t = 0 имеем точку O(0; 0):

С Ox : y(t) = 0 , t = 0: При t = 0 получаем ту же точку O(0; 0):

26

2) Бесконечные пределы функции x(t); y(t) имеют только при t ! 1 и только одновременно:

Это говорит о том, что вертикальных и горизонтальных асимптот у кривой нет. Выясним вопрос о наличии наклонных асимптот. Поскольку

27

что

x0(t) = 0 , t = 0;

p y0(t) = 0 , t = 0; t = 3 2:

На образовавшихся промежутках знаки x0(t) и y0(t) следующие:

4) Заполним таблицу, чтобы понять поведение кривой на полученных промежутках изменения параметра.

28

Значит, yxx00 > 0 при t 2 ( 1; 1), yxx00 < 0 при t 2 ( 1; 0) и t 2 (0; +1). 6) Решая следующую систему

получим, что на кривой нет точек самопересечения.

7) Переходим к построению эскиза параметрически заданной кривой. От-

мечаем на плоскости точки, через которые проходит кривая: O(0; 0) точка p !

второй ветви кривой. Далее, учитывая характер монотонности и направления выпуклости, рисуем параметрически заданную кривую (см. Рис. 16).

29

4 Индивидуальные задания

Исследовать функции и построить эскизы их графиков:

30