Графики

МИНОБРНАУКИ РОССИИ

Федеральное государственное автономное образовательное учреждение высшего профессионального образования

¾ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ¿

Д.А. Абанина, А.В. Кузьминова

МЕТОДИЧЕСКИЕ УКАЗАНИЯ для студентов первого курса факультета математики, механики и

компьютерных наук

ИССЛЕДОВАНИЕ ФУНКЦИЙ И ПОСТРОЕНИЕ ГРАФИКОВ

Ростов-на-Дону 2012

Введение

Методические указания предназначены для практических занятий по теме ¾Исследование функций и построение графиков¿, входящей в курс математического анализа, и состоят из четырех параграфов. Первый параграф содержит алгоритм полного исследования функции, а также необходимые понятия и теоретические результаты по каждому пункту алгоритма. Во втором параграфе подробно разобраны стандартные примеры на исследование функций и построение графиков. Третий параграф посвящен специальному разделу построению параметрически заданных кривых. Наконец, в четвертом параграфе приведено 15 наборов индивидуальных заданий для самостоятельной работы студентов.

1Алгоритм исследования функции. Необходимые теоретические сведения

Для того чтобы провести исследование функции y = f(x), необходимо выполнить следующие действия:

1.Найти область определения D(f) функции f. Выяснить, является ли функция четной, нечетной, периодической. Найти точки пересечения графика f функции f с осями координат.

2.Исследовать функцию f на непрерывность. Найти точки разрыва и установить их род. Указать вертикальные асимптоты, если они есть.

3.Найти наклонные асимптоты, если они есть.

4.Вычислить f0; исследовать функцию на экстремум, указать промежутки монотонности.

5.Вычислить f00; исследовать функцию на перегиб, указать направления выпуклости графика f функции f.

6.Нарисовать эскиз f .

Напомним коротко основные понятия и факты по пунктам приведенного алгоритма.

3

1.1 Общие свойства функции

Определение 1. Пусть даны два непустых числовых множества X и Y . Говорят, что задана функция f, действующая из X в Y , если определен закон (правило) f, по которому каждому элементу x 2 X ставится в соответствие единственный (вполне определенный) элемент y 2 Y , который обозначается f(x). При этом множество X называется областью определения функции f и обозначается D(f), а множество Y называется областью действия функции f.

Если функция задана аналитически, то есть формулой y = f(x), то под D(f) понимается ее естественная область определения, то есть множество тех x 2 R, для которых все участвующие в правой части операции определены.

Все функции делятся на четные, нечетные и функции общего вида.

Определение 2. Функция y = f(x) называется чётной, если ее область определения D(f) симметрична относительно 0 и f( x) = f(x) при всех x 2 D(f):

График четной функции симметричен относительно оси Oy. К четным функциям относится, например, f(x) = x2 (см. Рис. 1).

Определение 3. Функция y = f(x) называется нечётной, если ее область определения D(f) симметрична относительно 0 и f( x) = f(x) при всех x 2 D(f).

График нечетной функции симметричен относительно начала координат (0; 0). Примером нечетной функции служит f(x) = x (см. Рис. 2).

Функции, которые не являются ни четными, ни нечетными, называются функ-

4

циями общего вида. К функциям общего вида относятся, например:

1

1. f(x) = x 1, поскольку ее область определения D(f) = R n f1g несимметрична относительно 0;

2. f(x) = x2 x; так как f( x) = x2 + x не совпадает тождественно ни с f(x), ни с f(x):

Определение 4. Пусть T заданное положительное число. Функция f называется T -периодической, если ее область определения D(f) вместе с каждой своей точкой x содержит также точки x T и если при всех x 2 D(f)

f(x T ) = f(x) :

Примером периодической функции служит f(x) = sin x; T = 2 .

1.2 Непрерывность, точки разрыва, вертикальные асимптоты

Перейдем к исследованию функции на непрерывность. Мы не будем приводить стандартное определение непрерывности функции в точке. Напомним лишь, что если a 2 D(f) является предельной точкой D(f), то f непрерывна

в точке a тогда и только тогда, когда существует lim f(x) = f(a): Соответ-

x!a

ственно, для непрерывности функции f в точке a справа (слева) необходимо и достаточно, чтобы

На практике вывод о непрерывности рассматриваемой функции f обычно делается на основании известных фактов о непрерывности элементарных функций и теорем о действиях с непрерывными функциями. Например, функция f(x) = sin x2 2x непрерывна на R; поскольку sin x2 непрерывна на R как

суперпозиция двух непрерывных элементарных функций sin x и x2, а функция x

2x непрерывна на R как линейная. Функция f(x) = x 1 непрерывна на своей

области определения D(f) = R n f1g как дробно-рациональная функция, то есть функция, представимая в виде отношения двух многочленов.

К точкам разрыва функции f относятся те точки из D(f); в которых f не является непрерывной, а также двусторонние предельные точки D(f), не принадлежащие D(f). Например, функция f(x) = sgn x имеет разрыв в точке a = 0; так как D(f) = R и 0 2 D(f); но f не является непрерывной в 0: Для

5

функции f(x) = x1 областью определения D(f) является множество Rnf0g, так что a = 0 двусторонняя предельная точка D(f); не принадлежащая D(f). Значит, 0 точка разрыва этой функции.

Все точки разрыва делятся на точки разрыва 1-го и 2-го рода.

Определение 5. Точка разрыва a функции f называется точкой разрыва 1-го рода, если односторонние пределы lim f(x) существуют и конечны. При этом

1) a называется точкой устранимого разрыва, если односторонние пределы

совпадают, то есть если существует конечный lim f(x);

x!a

2) a называется точкой неустранимого разрыва, если lim f(x) 6= lim f(x).

Точка a называется точкой разрыва 2-го рода, если хотя бы один из односторонних пределов бесконечен или не существует.

Соответственно, для того чтобы определить род точки разрыва a, необходимо найти односторонние пределы lim f(x).

Данные вопросы неразрывно связаны также с исследованием на наличие у графика вертикальных асимптот. Напомним следующее определение.

Определение 6. Пусть a 2 R правосторонняя (левосторонняя) предельная точка D(f). Если lim f(x) = 1 (соответственно, lim f(x) = 1),

то прямая x = a называется правосторонней (левосторонней) вертикальной асимптотой графика функции f.

Из определения вытекает, что вертикальные асимптоты график f может иметь либо в точке разрыва 2-го рода функции f, либо в односторонней предельной точке области определения. Проиллюстрируем оба возможных случая примерами.

Пример 1. Найти вертикальные асимптоты графика функции

x

f(x) = x 1 :

x

Решение. Для функции f(x) = x 1 область определения D(f) = R n f1g.

Функция f непрерывна на R n f1g. Точка a = 1 не принадлежит D(f), но является двусторонней предельной точкой D(f). Значит, a = 1 точка разрыва

то a = 1 точка разрыва 2-го рода. Одновременно из этого вытекает, что прямая x = 1 двусторонняя вертикальная асимптота f (см. Рис. 3).

6

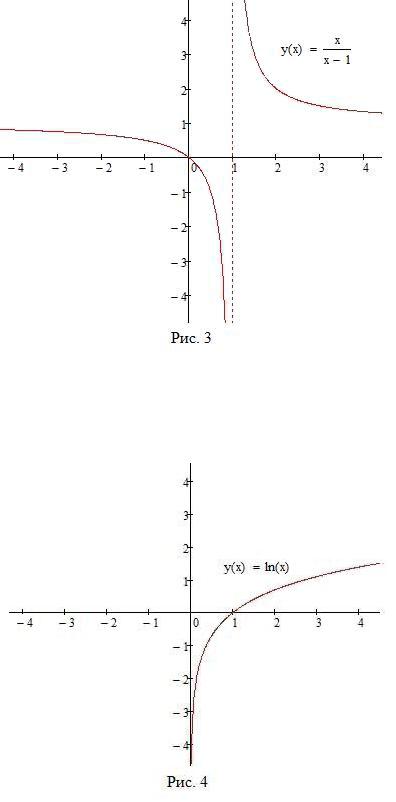
Пример 2. Найти вертикальные асимптоты графика функции f(x) = ln x.

Решение. Функция f(x) = ln x определена и непрерывна на (0; +1). Поскольку

lim f(x) = 1, то прямая x = 0 правосторонняя вертикальная асимптота

x!+0

7

f (см. Рис. 4).

1.3 Наклонные асимптоты

Определение 7. Пусть функция f определена в некоторой окрестности +1 (соответственно, 1). Прямая y = kx+b называется наклонной асимп-

Исследование на наличие наклонных асимптот проводится чаще всего с помощью следующего критерия.

Теорема 1 (критерий наклонной асимптоты). Пусть функция f определена в окрестности +1. Для того чтобы прямая y = kx + b была наклонной асимптотой f при x ! +1, необходимо и достаточно, чтобы существова-

Аналогично формулируется критерий наклонной асимптоты при x ! 1.

Пример 3. Найти наклонные асимптоты графика функции

f(x) = x2 3x 2 : x + 1

Решение. Область определения D(f) = R n f1g. Проведем сначала исследование на наличие наклонной асимптоты при x ! +1. Так как

8

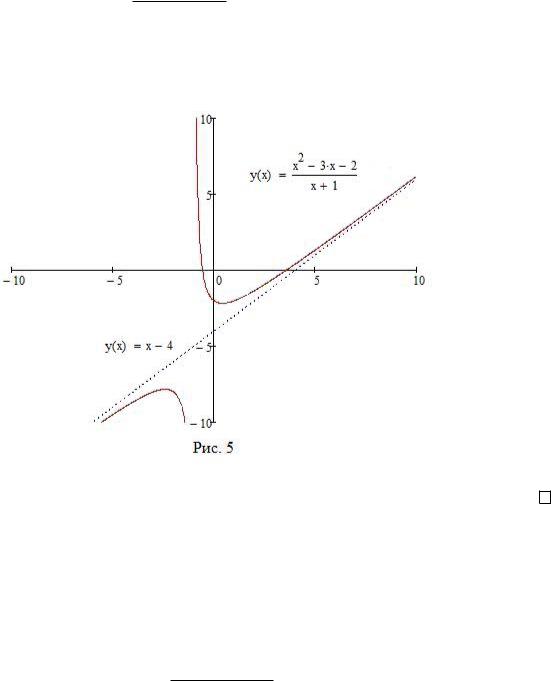
то прямая y = x 4 является наклонной асимптотой графика f функции f при x ! +1.

Легко видеть, что при x ! 1 никаких изменений не будет, то есть эта же прямая будет наклонной асимптотой при x ! 1 (см. Рис. 5).

Заметим, что в данном примере можно было легко найти наклонную асимптоту и с помощью определения. Именно, разделим числитель рассматриваемой неправильной дробно-рациональной функции на ее знаменатель:

f при x ! 1.

1.4 Производная, экстремумы, промежутки монотонности

Определение 8. Пусть функция y = f(x) определена в некоторой окрестности точки x0 и пусть x произвольная точка этой окрестности, отличная от x0. Если разностное отношение

f(x) f(x0)

x x0

9

имеет предел при x ! x0, то этот предел называется производной функции f в точке x0 и обозначается f0(x0) :

Дифференцируемость функции f в точке x0 означает наличие конечной производной f0(x0). На практике производные функций находятся в соответствии с таблицей производных элементарных функций и теоремами об операциях с дифференцируемыми функциями.

Промежутки монотонности заданной функции f, а также точки ее локального экстремума определяются, как известно, по поведению производной f0: Приведем сначала критерии монотонности функции на интервале.

Теорема 2 (критерий нестрогой монотонности). Пусть функция f дифференцируема на интервале (a; b). Для того чтобы f не убывала (не возраста-

ла) на (a; b), необходимо и достаточно, чтобы f0(x) 0 (соответственно, f0(x) 0) при всех x 2 (a; b).

Теорема 3 (критерий строгой монотонности). Если f дифференцируема на

(a; b), то f строго возрастает (строго убывает) на (a; b) тогда и только тогда, когда f0(x) 0 (f0(x) 0) при всех x 2 (a; b) и f0(x) не равна тожде-

ственному 0 ни на одном интервале ( ; ) (a; b):

Как известно, если функция f непрерывна на полусегменте или сегменте, дифференцируема внутри него, а для производной f0 во всех внутренних точках выполняются условия теоремы 2 или 3, то из этого можно сделать вывод о соответствующем характере монотонности f не рассматриваемом промежутке.

Перейдем к исследованию на локальный экстремум.

Определение 9. Точка a называется точкой локального максимума (минимума) функции f, если найдется окрестность (a ; a + ) точки a, для всех точек которой выполняется неравенство f(x) f(a) (соответственно, f(x) f(a)).

Точки локальных минимумов и локальных максимумов называются точками локальных экстремумов функции f. Значения функции f в этих точках называются экстремальными значениями.

В соответствии с теоремой Ферма, если a точка локального экстремума функции f и f дифференцируема в точке a, то f0(a) = 0. Однако, функция может и не быть дифференцируемой в точке экстремума (например, f(x) = jxj

10