

501(07) |
№ 4756 |
Р851 |
|
КАФЕДРА КОНСТРУИРОВАНИЯ ЭЛЕКТРОННЫХ СРЕДСТВ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное
автономное образовательное учреждение высшего профессионального образования «Южый федеральный университет» ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ В Г. ТАГАНРОГЕ
РУКОВОДСТВО К ЛАБОРАТОРНЫМ РАБОТАМ
по курсу
МЕТОДЫ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Для направлений:
211000 – конструирование и технология электронных средств,
210100 – электроника и наноэлектроника,
222900 – нанотехнологии и микросистемная техника.
ФЭП
Таганрог 2011
УДК 501(076.5)
Составители: И.В. Куликова, С.Н. Нелина, Е.А. Рындин
Руководство к лабораторным работам по курсу «Методы математической физики».-Таганрог: Изд-во ТТИ ЮФУ, 2011. – 52 с.
Цикл лабораторных работ по освоению студентами метода конечных разностей на основе пакета Matlab или Oktave подготовлен сотрудниками кафедры «Конструирования электронных средств» по дисциплине «Методы математической физики».
В работе приведены примеры для выполнения каждой лабораторной работы, с необходимыми комментариями и пояснениями, программы по численному решению дифференциальных уравнений в частных производных с использованием внутреннего языка Matlab. Приводятся варианты индивидуальных заданий и описание основных функций языка Matlab, используемых при написании программ.
Ил. 13 Библиогр.: 5 назв.
Рецензент К.А. Иванов, канд физ.-мат. наук, начальник отдела РОЦ НИЦ ТТИ ЮФУ
Введение
Многие задачи в инженерном анализе сводятся к решению краевых задач математической физики, с которыми в настоящее время приходится сталкиваться исследователям и инженерам. В большинстве случаев они не поддаются аналитическому решению, и единственная возможность их теоретического анализа — получение численного решения [1, 2].
Прогресс в разработке численных методов позволил существенно расширить круг решаемых задач. Задачи, решенные численными методами, используются практически во всех областях техники. Особенно велика их роль в таких областях, как нано- и микросистемная техника, нано- и микроэлектроника, где численные решения прочно вошли в практику.
Поскольку физические процессы лежат в основе функционирования всей техники и оказывают всеобъемлющее воздействие на человеческую жизнь, мы должны иметь возможность эффективно ими управлять. Эта возможность является следствием понимания физических процессов и их количественного описания. Эти знания позволяют конструктору выбирать из нескольких возможных конструкций оптимальную с безопасными и эффективными режимами работы.
В руководстве не рассматриваются уравнения математической физики, особенности задания граничных и начальных условий, методы дискретизации дифференциальных уравнений в частных производных. Вывод уравнений можно найти в соответствующих учебниках и методических пособиях [1 – 3]. В руководстве к лабораторным работам представлены основные этапы решения задач математической физики методом конечных разностей. Рассмотренный метод решения представлен в примерах для системы MATLAB с подробными комментариями, рекомендациями и описанием, от постановки задачи до кода программы и результатов решения поставленной задачи. В конце пособия представлены варианты заданий.
Разработанные лабораторные работы и задания к ним с подробным
3
описанием примеров и справочной информацией позволят студентам изучить математический аппарат, используемый для решения уравнений математической физики, внутренний язык MATLAB [3 - 5], и, в дальнейшем, самостоятельно разрабатывать программные продукты на основе метода конечных разностей. Приведенные примеры и задания соответствуют целям подготовки специалистов по направлениям «Конструирование и технология электронных средств», «Электроника и наноэлектроника», «Нанотехнологии и микросистемная техника».
4
Руководство к выполнению лабораторной работы № 1 «Решение одномерного стационарного уравнения теплопроводности»
Рассмотрим в качестве примера стационарную задачу нахождения температуры внутри стены здания. Так же в стене отсутствуют внутренние источники тепла и температура на границах не меняется во времени. Будем считать данную задачу одномерной, поскольку нас интересует как изменяется температура по толщине стены. Со стороны помещения
температура стены будет Tr , со стороны улицы Tenv . Распределение температуры будет описываться уравнением теплопроводности, которое в векторной форме имеет вид [2]:
ρ(x, y, z)C(x, y, z) |
∂T |
−div(k(x, y, z) grad (T ))= |
f (x, y, z), |
(1) |
|
∂t |
|||||
|
|
|
|
где ρ(x, y, z) - плотность; C(x, y, z) - удельная теплоемкость; k(x, y, z) -
коэффициент теплопроводности; f (x, y, z) - плотность источника тепла; T –
температура; t – время; x, y, z – координаты.
Для изотропной среды и одномерной стационарной задачи с учетом граничных условий в декартовой системе координат система уравнений будет иметь вид:
|
|
|
|
|
T (0)=T |
; |
|
||
|
|
0 |
|
|
T (L)=Tenv ; |
(2) |
|||
|
∂2T (x) |
= − f (x); |
|
|
k |
∂x |
2 |
|
|
|
|
|
|
|
где L – толщина стены.
В конечно-разностном виде система уравнений (2), на равномерной сетке на отрезке [0, L]с шагом ∆x будет следующей:
5
|
|
|
|
Ti =T0 , i =1; |
|
||
|
|
|
(3) |
Ti =Tenv , i = I; |
|||
|
Ti +1 −2Ti +Ti −1 |
|
|
k |
|
|
= − fi , i = 2KI −1; |
∆x |
2 |
||
|
|
|
|
где I – количество точек по длине.
Система уравнений (3) представляет собой систему линейных алгебраических уравнений (СЛАУ), матрица коэффициентов которой, например для 6 точек, будет иметь вид:
|
1 |
|
|
0 |
|
|
|
0 |
|
|
|
0 |
|
|
|
0 |
|
|
0 |
|
|
|
|
k |
− |
2k |
|
|
k |
|
|
0 |
|
|
|
0 |
|
|
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
∆x2 |
∆x2 |
∆x2 |
|
|
|
|
|
|
|
|||||||||||||
|
0 |
|
|
k |
|
− |
2k |
|
|
k |
|
|
|
0 |
|
|
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
∆x2 |
∆x2 |
|
∆x2 |
|
|
|
|
|
|||||||||||||
A = |
|
|
|
|
|
|
|
k |
|
|
|
|
|
, |
||||||||
|
0 |
|
|
0 |
|
|
|
k |
− |
2k |
|
|
|
|
0 |
|
|
|||||
|
|
|
|
|
∆x2 |
|
∆x2 |
|
∆x2 |
|
|
|
|
|||||||||
|
0 |
|
|
0 |
|
|
|
0 |
|
|
|
k |
− |
2k |
|
k |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
∆x2 |
∆x |
2 |
|
∆x2 |
|
|||||||||||
|
0 |
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
1 |
|
|
||||
вектор-столбец свободных членов B будет следующим:
T0− f2− f3 B = − f3 ,− f4− f5
Tenv
а вектор-столбец переменных T
T1
T2
T = T3 .
T4
T5
T6
(4)
(5)
(6)
6
В данной задаче нет источников тепла, поэтому fi = 0 .
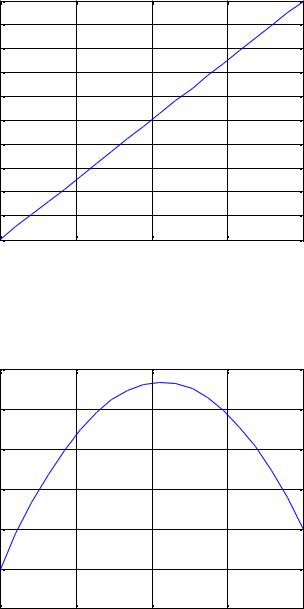
Ниже приведен один из вариантов кода программы, позволяющей решить СЛАУ (3) и вывести результаты решения, которые приведены на рисунке 1.
close all clear all
% Решение уравнения теплопроводности
k=120; |
% удельная теплоемкость Si (Вт/м/К) |
|
f=0; |
% плотность мощности |
источника тепла Вт/м^3 |
L=20e-2; |
% толщина стенки (м) |
х=0 |
Tenv=300; |
% температура (К)при |
|
T0=310; |
%температура (К) при |
х=L |
% Создание |
геометрии |
|
N=20; |
% число точек по толщине; |
|
dx=L/(I-1); |
|
|
X=0:dx:L; |
|
|
%Решение СЛАУ a=zeros(I,I); b=zeros(1,I); for i=2:I-1
a(i,i) =-k*2/dx^2; a(i,i+1)=k/dx^2; a(i,i-1)=k/dx^2; b(i) =f;
end
%граничные условия i=1;
a(i,i) = 1; b(i) = Tenv; i=I;
a(i,i) = 1; b(i) = T0; T=b/a'; plot(X,T) grid on xlabel('m') ylabel('K')
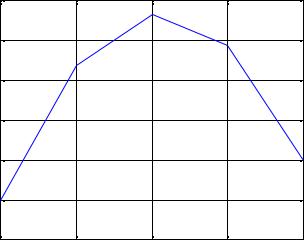
На рисунках 2-4 приведено распределение температуры при наличии внутренних источников тепла и граничных условиях, приведенных выше, для различного числа точек I = 30 – рисунок 2, I = 5 – рисунок 3 и I = 3 – рисунок
4.
7
310 |
|
|
|
|
309 |
|
|
|
|
308 |
|
|
|
|
307 |
|
|
|
|
306 |
|
|
|
|
K 305 |
|
|
|
|
304 |
|
|
|
|
303 |
|
|
|
|
302 |
|
|
|
|
301 |
|
|
|
|
3000 |
0.05 |
0.1 |
0.15 |
0.2 |
|
|
m |
|
|
|
|
Рисунок 1 |
|
|
|
350 |
|
|
|
|
|
340 |
|
|
|
|
|
330 |
|
|
|
|
K |
320 |
|
|
|
|
|
310 |
|
|
|
|
|
300 |
|
|
|
|
|
2900 |
0.05 |
0.1 |
0.15 |
0.2 |
|
|
|
m |
|
|
Рисунок 2. Распределение температуры при наличии источников тепла, I = 30.
8
|
350 |
|
|
|
|
|
340 |
|
|
|
|
|
330 |
|
|
|
|
K |
320 |
|
|
|
|
|
310 |
|
|
|
|
|
300 |
|
|
|
|
|
2900 |
0.05 |
0.1 |
0.15 |
0.2 |
|
|
|
m |
|
|
Рисунок 3. Распределение температуры при наличии источников тепла, I = 5
9

Руководство к выполнению лабораторной работы № 2 «Решение двумерного стационарного уравнения теплопроводности»
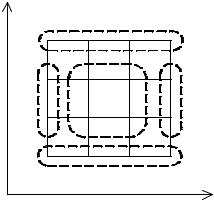
Рассмотрим в качестве примера задачу нахождения распределения температуры в балке с поперечным сечением, показанным на рисунке 5. На границах балки зададим граничные условия 1 рода – температуру Tenv .
Данная задача будет двумерной и стационарной, поскольку нас интересует, как изменяется температура по сечению балки.
y
Ly |
|
|
J |
Tenv |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Tenv |
f |
|
Tenv |
|
|
|
|
|
|
|
|
|
||
0 |
|
|
1 |
|
Tenv |
|
|
|
|
|
|
|
|
||||
|
|
1 |
I |
i |
||||
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
Lx |
x |
|||
Рисунок 5 - Двумерная модель
Для изотропной среды и двумерной стационарной задачи с учетом граничных условий в декартовой системе координат система уравнений будет иметь вид:
T (0, y)=Tenv ; |
|
|
|
||
T (Lx, y)=T |
; |
|
|
||
|
|
env |
|
|
|
T (x, 0)=Tenv ; |
|
|
(7) |
||
T (x, Ly)=T |
; |
|
|||
|
∂2T (x, y) |
env |
|
∂2T (x, y) |
|
|
+ k |
= − f (x, y); |
|||
k |
∂x2 |
∂y2 |
|||
|
|
|
|
||
где Lx, Ly – габариты поперечного сечения балки.
10
В конечно-разностном виде система уравнений (7), на равномерной
сетке с шагом ∆x и ∆y будет следующей:
1 грань: Ti, j =Tenv , i = 2KI −1, |
j =1; |
||||
|
|
|
|
|
|
2 грань: Ti, j =Tenv , i =1, j =1KJ; |
|||||
|
|
|
|
j = J; |
|
3 грань: Ti, j =Tenv , i = 2KI −1, |
|||||
|
|
|
|
|
|
4 грань: Ti, j =Tenv , i = I, j =1KJ; |
|||||
k Ti +1, |
j −2Ti, j +Ti −1, j +k Ti, j +1 −2Ti, j +Ti, j −1 |
||||
|
|
∆x2 |
|
|
∆y2 |
|
|||||
(8)
= −fi, j , i = 2KI −1, j = 2KJ −1;
где I, J – количество точек по координатам x и y, соответственно. Количество точек соответствует количеству уравнений. Для
наглядности, на рисунке 6 показано каким точкам какие уравнения соответствуют в системе уравнений (8).
y, j |
3 |
2 |
4 |
|
1 |
x, i
Рисунок 6.
Стоит обратить внимание, что вектор-столбец неизвестных T должен имеет размерность 1× IJ , а в системе уравнений (8) его размерность I × J . Прежде чем выписывать коэффициенты матрицы A необходимо перенумеровать точки. Введем новый индекс n, который будет изменятся от 1 до N = IJ , а выражения для пересчета точек с различными индексами будут иметь следующий вид:
11
|
|
|
|
|
|
|
i, j |
|
|
|
n = i +(j −1)I |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
i +1, j n′ = n +1 = i +1 +(j −1)I |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
i −1, j |
n′ = n −1 = i −1 +(j −1)I , |
|
|
|
|
|
(9) |
||||||||||||
|
|
|
|
|
|
|
i, j +1 n′ = n + I = i + jI |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
i, j −1 n′ = n − I = i +(j −2)I |
|
|
|
|
|
|
|||||||||||||
Система уравнений (8) представляет собой СЛАУ, матрица |
||||||||||||||||||||||||||
коэффициентов которой, например для 4 ×4 точек, будет иметь вид: |
|
|
||||||||||||||||||||||||
1 |
0 |
0 |
0 |
|
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
||||||||
|
|
1 |
0 |
0 |
|
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
|
|
||||||
0 |
|
|
|
0 |
||||||||||||||||||||||
|
|
0 |
1 |
0 |
|
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
|
|
||||||
0 |
|
|
|
0 |
||||||||||||||||||||||
0 |
0 |
0 |
1 |
|
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
||||||||
0 |
0 |
0 |
0 |
|
1 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
||||||||
|
|
ay |
0 |
0 |
|
ax aii |
ax |
0 |
0 |
ay |
|
0 |
0 |
0 |
0 |
0 |
|
|
||||||||
0 |
|
|
0 |
|||||||||||||||||||||||
0 |
0 |
ay |
0 |
|
0 |
|
ax |
aii |
|
ax |
0 |
0 |
|
ay |
0 |
0 |
0 |
0 |
0 |
|||||||
|
|
0 |
0 |
0 |
|
0 |
|
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
|
|
||||||
0 |
|
|
|
0 |
||||||||||||||||||||||
A = |
0 |
0 |
0 |
0 |
|
0 |
|
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
||||||
|
|
|
|
|
||||||||||||||||||||||
|
0 |
0 |
0 |
|
0 |
|
ay |
0 |
0 |
ax |
aii |
|
ax |
0 |
0 |
ay |
0 |
|
||||||||
0 |
|
|
|
0 |
||||||||||||||||||||||
|
|
0 |
0 |
0 |
|
0 |
|
0 |
ay |
0 |
0 |
ax |
|
aii |
ax |
0 |
0 |
ay |
|
|
||||||
0 |
|
|
|
0 |
||||||||||||||||||||||
|
|
0 |
0 |
0 |
|
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
|
|
||||||
0 |
|
|
|
0 |
||||||||||||||||||||||
0 |
0 |
0 |
0 |
|
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
||||||||
0 |
0 |
0 |
0 |
|
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
0 |
||||||||
|
|
0 |
0 |
0 |
|
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
|
, (10) |
||||||
0 |
|
|
|
0 |
||||||||||||||||||||||
|
|
0 |
0 |
0 |
|
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
|
|
||||||
0 |
|
|
|
1 |
||||||||||||||||||||||
|
|
|
|
2k |
|
2k |
|
|
|
|
k |
|
, ay = |
|
k |
|
|
|
|
|
|
|
|
|||
где aii |
= − |
+ |
|
, |
ax = |
|
|
|
|
, |
|
|
|
|
|
|
||||||||||
|
|
|
|
∆x |
2 |
|
|
∆y |
2 |
|
|
|
|
∆x |
2 |
|
|
∆y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
вектор-столбец свободных членов B будет следующим: |
|
|
|
|||||||||||||||||||||||
|
|
|
|
[Tenv |
|
Tenv |
|
|
Tenv |
|
Tenv |
Tenv |
|
− f |
− f |
Tenv |
|
|
|
|||||||
|
|
|
B =T |
|
|
− f |
|
|
− f |
T |
|
T |
|
T |
|
T |
|
T |
]. |
|
|
(11) |
||||
|
|
|
|
env |
|
|
|
|
|
|
|
env |
|
env |
|
env |
env |
env |
|
|
|
|
||||
В данной задаче есть источник тепла (например, при протекании электрического тока), плотность мощности которого равномерно распределенный по площади поперечного сечения балки.
Ниже приведен один из вариантов кода программы, позволяющей
12
решить данную СЛАУ и вывести результаты решения, которые представлены
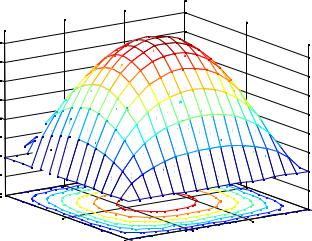
на рисунке 7.
close all |
|
|
clear all |
|
уравнения теплопроводности |
% Решение |
|
|
k=120; |
% |
% удельная теплоемкость Si (Вт/м/К) |
f=1e6; |
плотность мощности источника тепла Вт/м^3 |
|
Lx=20e-2; |
|
|
Ly=30e-2; |
|
% температура (К) |
Tenv=300; |
|
|
% Создание |
геометрии |
|
I=15; |
|
% число точек по x; |
J=17; |
|
% число точек по y; |
dx=Lx/(I-1); dy=Ly/(J-1); X=0:dx:Lx; Y=0:dy:Ly;
%Решение СЛАУ
N=I*J;
a=zeros(N,N);
b=zeros(1,N); for i=2:I-1
for j=2:J-1 n=i+(j-1)*I;
a(n,n) =-k*2/dx^2-k*2/dy^2; a(n,n+1)=k/dx^2; a(n,n-1)=k/dx^2; a(n,n+I)=k/dy^2; a(n,n-I)=k/dy^2;
b(n) =-f;
end
end
%граничные условия
for j=1:J i=1;
n=i+(j-1)*I; a(n,n) = 1; b(n) = Tenv; i=I; n=i+(j-1)*I; a(n,n) = 1; b(n) = Tenv;
end
for i=2:I-1 j=1; n=i+(j-1)*I; a(n,n) = 1;
b(n) = Tenv; j=J; n=i+(j-1)*I; a(n,n) = 1;
13
b(n) = Tenv;
end
TT=b/a';
T=zeros(I,J); for i=1:I
for j=1:J T(i,j)=TT(i+(j-1)*I);
end
end
meshc(Y,X,T) grid on xlabel('y, m') ylabel('x, m') zlabel('K')
axis([min(Y) max(Y) min(X) max(X) (min(min(T))-10) max(max(T))])
K
330
325
320
315
310
305 

 300
300 

 295
295 


290 
0.2
0.1 |
0.3 |
0.2 |
|
0 |
0.1 |
0 |
|
x, m |
y, m |
|
Рисунок 7 – Распределение температуры балке с поперечным квадратным сечением и источником тепла
14
Руководство к выполнению лабораторной работы № 3 «Решение трехмерного стационарного уравнения теплопроводности»
Рассмотрим в качестве примера трехмерную задачу нахождения распределения температуры в балке с поперечном квадратным сечением. На рисунке 8 представлена нумерация стенок балки и направление координатных осей. На границах 1, 2, 3 зададим граничные условия 1 рода – температуру Tenv , на границах 4, 5, 6 граничные условия 2 рода – адиабатическую стенку ( qΩ = 0 ).
3
2
6
5
y |
1 |
|
z |
|
|
|
4 |
|
|
|
|
|
|
x |
Рисунок 8 – Модель балки с поперечным квадратным сечением
На 4, 5, 6 границах задан тепловой поток, который по закону Фурье можно представить в следующем виде:
q = −k |
∂T |
, |
(12) |
|
∂n |
||||
|
|
|
где n – нормаль к поверхности.
Для изотропной среды и трехмерной стационарной задачи с
граничными условиями, учитывая нормали в декартовой системе координат, 15
система уравнений будет иметь вид:
1 грань: T (x, y, 0)=Tenv ; |
|
|
|
|
|
|
|
||||||
2 |
грань: T (x, y, Lz)=T |
; |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
env |
|
|
|
|
|
|
|
|
грань: T (x, Ly, z)=Tenv ; |
|
|
|
|
|
|
||||||
3 |
|
|
|
|
|
|
|||||||
|
|
|
|
(x, 0, z) |
= 0; |
|
|
|
|
|
|
|
|
4 грань: ∂T |
|
|
|
|
|
|
|
||||||
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
грань: ∂T |
(Lx, y, z)= 0; |
|
|
|
(13) |
|||||||
5 |
|
|
|
||||||||||
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
∂T |
|
|
|
|
|
|
|
|
|
|
|
грань: |
(0, y, z) |
|
|
|
|
|
|
|
|
|
||
6 |
|
∂x |
= 0; |
|
|
|
|
|
|
|
|||
∂2T (x, y, z) |
+ ∂2T (x, y, z) |
+ |
∂2T (x, y, z) |
= − |
f (x, y, z) |
; |
|||||||
|
2 |
|
|||||||||||
|
∂x |
2 |
|
∂y |
2 |
|
|
∂z |
|
k |
|||
|
|
|
|
|
|
|
|
||||||
где Lx, Ly, Lz – габариты балки.
В конечно-разностном виде система уравнений (13), на равномерной сетке с шагом по соответствующим осям координат ∆x , ∆y , ∆z будет следующей:
Ti, j,n =Tenv , |
i =1KI , |
|
j =1KJ , |
n =1 |
|||||||
Ti, j,n =Tenv , |
i =1KI , |
|
j =1KJ , |
n = N |
|||||||
Ti, j,n =Tenv , |
i = 2KI −1, |
j = J |
n = 2KN −1; |
||||||||
Ti, j +1,n −Ti, j,n |
= 0; i = 2KI −1, |
j =1 |
n = 2KN −1; |
||||||||
|
|
∆y |
|||||||||
|
|
|
|
|
|
|
|
|
|
||
Ti, j,n −Ti −1, j,n |
= 0; i = I , |
|
j =1KJ , n = 2KN −1; |
||||||||
|
|
∆x |
|
||||||||
|
|
|
|
|
|
|
|
|
|
||
Ti +1, j,n −Ti, j,n |
= 0; i =1, |
|
j =1KJ , n = 2KN −1; |
||||||||
|
|
∆x |
|
||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
Ti −1, j,n −2Ti, j,n +Ti +1, j,n |
+ |
Ti, j −1,n −2Ti, j,n +Ti, j +1,n |
+ |
||||||
|
|
|
|
∆x2 |
|
|
∆y2 |
|
|
||
|
+ |
Ti, j,n −1 −2Ti, j,n +Ti, j,n +1 |
|
= − |
fi, j,n |
, |
(14) |
||||
|
|
|
|||||||||
|
|
|
|
∆z2 |
|
k |
|
|
|||
i = 2KI −1, j = 2KJ −1, n = 2KN −1;
где I, J, К – количество точек по координатам x, y, z соответственно.
Стоит обратить внимание, что вектор-столбец переменных T должен имеет размерность 1×IJN , а в системе уравнений (14) размерность матрицы
16
неизвестных I × J × N . Прежде чем выписывать коэффициенты матрицы A необходимо перенумеровать точки. Введем новый индекс l, который будет изменятся от 1 до L = NIJ , а выражения для пересчета индексов будут иметь следующий вид:
i, j, n |
l = i +(j −1)I +(n −1)IJ |
|
|
i +1, j, n |
l′ = l +1 = i +1 +(j −1)I +(n −1)IJ |
|
|
i −1, j, n |
l′ = l −1 = i −1 +(j −1)I +(n −1)IJ |
|
|
i, j +1, n |
l′ = l + I = i + jI +(n −1)IJ |
, |
(15) |
i, j −1, n |
l′ = l − I = i +(j −2)I +(n −1)IJ |
|
|
i, j, n +1 |
l′ = l + IJ = i +(j −2)I + nIJ |
|
|
i, j, n −1 |
l′ = l − IJ = i +(j −2)I +(n −2)IJ |
|
|
Система уравнений (14) представляет собой СЛАУ, матрица коэффициентов А и вектор столбец B которой, будут иметь вид:
i = 2KI −1, j = 2KJ −1, n = 2KN −1; |
|
||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2 |
|
+ |
|
|
2 + |
|
2 |
|
|
|
|
|
|
|
||||||
A(l, l)= − |
∆x |
|
|
∆y |
∆z |
|
, |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
A(l, l +1)= |
|
|
|
1 |
|
|
, |
A(l, l −1)= |
1 |
|
, |
|
|
|
|
||||||||||
|
∆x2 |
|
∆x2 |
|
|
|
(16) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
A(l, l + I )= |
|
|
1 |
|
|
, A(l, l − I )= |
1 |
|
, |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
∆y2 |
∆y2 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
A(l, l + IJ )= |
|
|
1 |
|
, A(l, l − IJ )= |
|
1 |
|
, |
|
|||||||||||||||
|
∆z2 |
∆z2 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
B(l, l)= − |
fi, j,n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A(l,l )=1, B(l )=Tenv : |
|
|
|
|
|
|
|
|
|
|
i =1KI , |
|
|
|
|
|
j =1KJ , |
n =1; |
|||||||
A(l,l )=1, B(l )=Tenv : |
|
|
|
|
|
|
|
|
|
|
i =1KI , |
|
|
|
|
|
j =1KJ , |
n = N; |
|||||||
A(l,l )=1, B(l )=Tenv : |
|
|
|
|
|
|
|
|
|
|
i = 2KI −1, |
|
|
j = J , |
n = 2KN −1; |
||||||||||
A(l,l )= −1, A(l,l + I )=1, B(l )= 0 : i = 2KI −1, |
|
|
j =1, |
n = 2KN −1; |
|||||||||||||||||||||
A(l,l )= −1, A(l,l −1)=1, B(l )= 0 : i = I , |
|
|
|
|
|
|
|
j =1KJ , n = 2KN −1; |
|||||||||||||||||
A(l,l )= −1, A(l,l +1)=1, B(l )= 0 : i =1, |
|
|
|
|
|
|
|
j =1KJ , n = 2KN −1; |
|||||||||||||||||
Ниже приведен один |
|
из |
|
вариантов |
|
кода |
|
программы, позволяющей |
|||||||||||||||||
решить данную СЛАУ и вывести результаты решения.
17
close all |
|
clear all |
уравнения теплопроводности |
% Решение |
|
k=120; |
% коэффициент теплопроводности Si (Вт/м/К) |
f=-1e5; |
% плотность источника тепла Вт/м^3 |
Lx=20e-2; |
|
Ly=30e-2; |
|
Lz=50e-2;
Tenv=300; % температура (К)
% Создание |
сетки |
I=15; |
% число точек по x; |
J=17; |
% число точек по y; |
S=17; |
% число точек по t; |
dx=Lx/(I-1); |
|
dy=Ly/(J-1); |
|
dz=Lz/(S-1); |
|
X=0:dx:Lx; |
|
Y=0:dy:Ly; |
|
Z=0:dz:Lz;
%Заполнение коэффициентов матрицы А и В
N=I*J*S;
a=zeros(N,N);
b=zeros(1,N); for s=2:S-1
for i=2:I-1
for j=2:J-1 n=i+(j-1)*I+(s-1)*I*J;
a(n,n) =k*2/dx^2+k*2/dy^2+k*2/dz^2; a(n,n+1)=-k/dx^2;
a(n,n-1)=-k/dx^2; a(n,n+I)=-k/dy^2; a(n,n-I)=-k/dy^2; a(n,n-I*J)=-k/dz^2; a(n,n+I*J)=-k/dz^2; b(n)= -f;
end
end
end
% граничные условия for i=1:I
for j=1:J s=1;
n=i+(j-1)*I+(s-1)*I*J; a(n,n) = 1;
b(n) = Tenv; s=S;
n=i+(j-1)*I+(s-1)*I*J; a(n,n) = 1;
b(n) = Tenv;
end
end
for i=2:I-1 for s=2:S-1
18
j=J; n=i+(j-1)*I+(s-1)*I*J; a(n,n) = 1;
b(n) = Tenv; j=1;
n=i+(j-1)*I+(s-1)*I*J; a(n,n) = -1;
a(n,n+I) = 1;
end
end
for s=2:S-1 for j=1:J
i=1; n=i+(j-1)*I+(s-1)*I*J; a(n,n) = -1;
a(n,n+1) = 1; i=I;
n=i+(j-1)*I+(s-1)*I*J; a(n,n) = -1;
a(n,n-1) = 1;
end
end
% Решение СЛАУ
TT=b/a';
T=zeros(I,J,S); for s=1:S
for i=1:I
for j=1:J T(i,j,s)=TT(i+(j-1)*I+(s-1)*I*J);
end
end
end
%Вывод графиков по слоям по оси Z for s=1:S
figure mesh(Y,X,T(:,:,s)) grid on xlabel('y, m') ylabel('x, m') zlabel('T, K')
axis([min(Y) max(Y) min(X) max(X) (min(min(min(T)))) max(max(max(T)))])
pause (0.1)
end
%Вывод 3D графика
figure
slice(Y, X, Z, T, [Y(fix(3*J/4))], [X(fix(3*I/4))], [Z(fix(S/2))], length(X))
grid on colorbar xlabel('y, m') ylabel('x, m') zlabel('z, m') title('T, K')
19
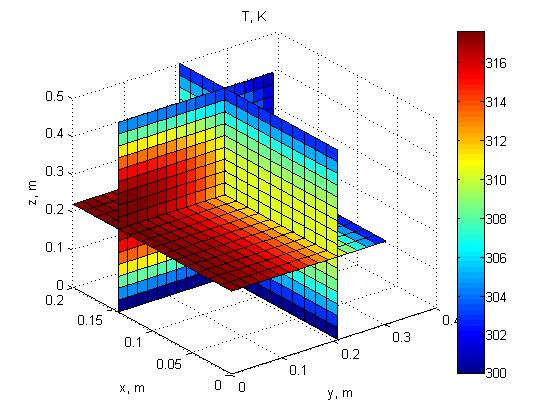
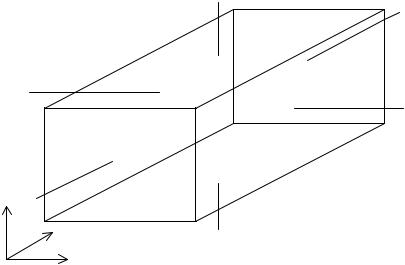
Рисунок 10 – Распределение температуры в трехмерной структуре
20
Руководство к выполнению лабораторной работы № 4 «Решение двумерного нестационарного уравнения теплопроводности»
Рассмотрим в качестве примера задачу нахождения распределения температуры в однородной балке с прямоугольным поперечным сечением при нагреве (стационарный случай рассмотрен во 2 лабораторной работе). На границах сечения балки зададим граничные условия 1 рода – температуру Tenv . Данная задача будет двумерной и нестационарной.
Для однородной среды, двумерной и нестационарной задачи с учетом граничных и начальных условий в декартовой системе координат система уравнений будет иметь вид:
T (x, y, 0)=Tenv ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
T (0, y. t ) |
=T |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
env |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T (Lx, y, t )=Tenv ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
T (x, 0, t ) |
=T |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(17) |
|||||
|
|
|
|
|
|
env |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
T (x, Ly, t )=T |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
∂T (x, y, t ) |
env |
|
∂2T (x, y, t ) |
|
∂ |
2T (x, y, t ) |
|
|
|||||||||||||||
|
|
|
|
(x, y). |
||||||||||||||||||||
cρ |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
+ |
|
|
|
2 |
|
|
||||
|
|
|
∂t |
|
|
−k |
|
|
∂x |
|
∂y |
|
= f |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
В конечно-разностном виде система уравнений (17), на равномерной |
||||||||||||||||||||||||
сетке с шагом ∆x , ∆y и ∆t для будет следующей: |
|
|
|
|||||||||||||||||||||
|
T |
|
|
=T |
|
, i =1KI , j =1KJ |
, n =1; |
|
|
|
||||||||||||||
|
|
i, j,n |
|
env |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Ti, j,n |
=Tenv , i =1, |
j =1KJ , n = 2KN; |
|
|
|||||||||||||||||||
|
T |
|
|
=T |
|
, i = I , j =1KJ , n = 2KN; |
|
|
||||||||||||||||
|
|
i, j,n |
|
env |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Ti, j,n |
=Tenv , i = 2KI −1, |
j =1, n = 2KN; |
|
||||||||||||||||||||
|
T |
|
|
=T |
|
, i = 2KI −1, j = J |
, n = 2KN; |
|
||||||||||||||||
|
|
i, j,n |
|
env |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(18) |
|||
|
|
|
|
T |
|
−T |
|
|
|
T |
|
|
|
− |
2T |
|
|
+T |
|
|||||
|
|
|
|
i, j,n |
|
|
i, j,n −1 |
i +1, j,n |
|
i, j,n |
i −1, j,n |
|
||||||||||||
|
cρ |
|
|
|
|
|
|
|
|
−k |
|
|
|
|
|
|
|
|
|
+ |
||||
|
|
|
∆t |
|
|
|
|
|
|
|
|
|
∆x |
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Ti, j +1,n −2Ti, j,n |
+Ti, j −1,n |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= − fi, j,n , |
|
|
|
|||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
∆y |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i = 2KI −1, j = 2KJ −1, n = 2KN; |
|
|
|
||||||||||||||||||||
21
где I, J, N– количество точек по координатам x, y и времени, соответственно. Стоит обратить внимание, что вектор-столбец переменных T должен имеет размерность 1×IJN , а в системе уравнений (17) размерность матрицы неизвестных I × J × N . Прежде чем выписывать коэффициенты матрицы A необходимо перенумеровать точки. Введем новый индекс l, который будет изменятся от 1 до L = NIJ , а выражения для пересчета индексов будут иметь
следующий вид:
i, j, n |
l = i +(j −1)I +(n −1)IJ |
|
|
||
i +1, j, n |
l′ = l +1 = i +1 +(j −1)I +(n −1)IJ |
|
|
||
i −1, j, n |
l |
′ |
= l −1 = i −1 +(j −1)I +(n −1)IJ |
, |
(19) |
|
|||||
i, j +1, n |
l′ = l + I = i + jI +(n −1)IJ |
|
|
||
i, j −1, n |
l′ = l − I = i +(j −2)I +(n −1)IJ |
|
|
||
i, j, n −1 |
l′ = l − IJ = i +(j −2)I +(n −2)IJ |
|
|
||
Система уравнений (18) представляет собой СЛАУ, коэффициентов А и вектор столбец B которой, будут иметь вид:
i = 2KI −1, j = 2KJ −1, n = 2KN ,
A(l, l )= |
cρ |
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
2 + |
|
2 |
|
|
|
|
|
|
|||||||
∆t |
−k |
∆x |
∆y |
, |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
A(l, l +1)= |
|
k |
|
, A(l, l −1)= |
|
k |
|
, |
|
|
|||||||||
∆x2 |
∆x2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
A(l, l + I )= |
|
k |
, A(l, l − I )= |
k |
|
, |
|
||||||||||||
|
∆y2 |
∆y2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
A(l, l − IJ )= − |
cρ |
, |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
∆t |
|
|
|
|
|
|
|
|
|
|
|
|||
B(l, l )= fi, j,n ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
A(l, l )=1, B(l )=Tenv : |
|
i =1KI , |
|
|
|
j =1KJ , |
n =1 |
||||||||||||
A(l, l )=1, B(l )=Tenv : |
|
i =1 |
|
|
|
|
|
j =1KJ , |
n = 2KN; |
||||||||||
A(l, l )=1, B(l )=Tenv : |
|
i = I |
|
|
|
|
|
j =1KJ , |
n = 2KN; |
||||||||||
A(l, l )=1, B(l )=Tenv : |
|
i = 2KI −1, |
|
|
j =1 |
|
|
n = 2KN; |
|||||||||||
A(l, l )=1, B(l )=Tenv : |
|
i = 2KI −1, |
|
|
j = J |
|
n = 2KN. |
||||||||||||
матрица
(19)
Ниже приведен один из вариантов кода программы, позволяющий
22
решить СЛАУ (19) и вывести результаты решения, которые приведены на рисунке 12 и 13.
close all |
|
clear all |
уравнения теплопроводности |
% Решение |
|
k=120; |
% коэффициент теплопроводности Si (Вт/м/К) |
ro=2330; |
% плотность (кг/м^3) |
c=800; |
% удельная теплоемкость Дж/(кг*К) |
f=-1e6; |
% плотность источника тепла Вт/м^3 |
Lx=20e-2; |
|
Ly=30e-2; |
|
Lt=300; |
% температура (К) |
Tenv=300; |
|
% Создание |
геометрии |
I=11; |
% число точек по x; |
J=12; |
% число точек по y; |
S=17; |
% число точек по t; |
dx=Lx/(I-1); dy=Ly/(J-1); dt=Lt/(S-1); X=0:dx:Lx; Y=0:dy:Ly; time=0:dt:Lt;
%Заполнение матриц коэффициентов
N=I*J*S;
a=zeros(N,N);
b=zeros(1,N);
%Начальные условия
s=1;
for i=1:I for j=1:J
n=i+(j-1)*I+(s-1)*I*J; a(n,n)=1;
b(n)=Tenv;
end
end
for s=2:S
for i=2:I-1
for j=2:J-1 n=i+(j-1)*I+(s-1)*I*J;
a(n,n) =ro*c/dt+k*2/dx^2+k*2/dy^2; a(n,n+1)=-k/dx^2;
a(n,n-1)=-k/dx^2; a(n,n+I)=-k/dy^2; a(n,n-I)=-k/dy^2; a(n,n-I*J)=-ro*c/dt; b(n) =-f;
end
end
% граничные условия for j=1:J
i=1;
23
n=i+(j-1)*I+(s-1)*I*J; a(n,n) = 1;
b(n) = Tenv; i=I;
n=i+(j-1)*I+(s-1)*I*J; a(n,n) = 1;
b(n) = Tenv;
end
for i=2:I-1 j=1;
n=i+(j-1)*I+(s-1)*I*J; a(n,n) = 1;
b(n) = Tenv; j=J;
n=i+(j-1)*I+(s-1)*I*J; a(n,n) = 1;
b(n) = Tenv;
end
end
% Решение СЛАУ
TT=b/a';
T=zeros(I,J,S);
Ttime=zeros(1,S); for s=1:S
for i=1:I
for j=1:J T(i,j,s)=TT(i+(j-1)*I+(s-1)*I*J);
end
end
end
for s=1:S figure
meshc(Y,X,T(:,:,s)) grid on
xlabel('y, m') ylabel('x, m') zlabel('T, K')
axis([min(Y) max(Y) min(X) max(X) (min(min(min(T)))-10) max(max(max(T)))])
pause (0.1) M(s)=getframe;
end figure
movie(M,5,3) for s=1:S
Ttime(s)=T(ceil(I/2),ceil(J/2),s);
end figure
plot(time,Ttime) grid on xlabel('t, c') ylabel('T, K')
24
T, K
330
320
310
300 





290
0.2
0.15 |
0.3 |
0.1 |
0.2 |
0.050.1
x, m |
0 0 |
y, m |
|
|
T, K
330
320
310 







 300
300 










290 0.2
0.15 |
0.3 |
0.1 |
0.2 |
0.050.1
x, m |
0 0 |
y, m |
|
|
а) |
б) |
T, K
330
320
310
300 

290 







 0.2
0.2 



0.15 |
|
0.3 |
0.1 |
|
0.2 |
0.05 |
|
0.1 |
x, m |
0 0 |
y, m |
|
|
в)
Рисунок 12. Распределение температуры в различные моменты времени. а – в начальный момент времени, б – через 40 секунд, в – через 200 секунд.
|
335 |
|
|
|
|
|
|
|
330 |
|
|
|
|
|
|
|
325 |
|
|
|
|
|
|
|
320 |
|
|
|
|
|
|
K |
315 |
|
|
|
|
|
|
T, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
310 |
|
|
|
|
|
|
|
305 |
|
|
|
|
|
|
|
300 |
|
|
|
|
|
|
|
2950 |
50 |
100 |
150 |
200 |
250 |
300 |
|
|
|
|
t, c |
|
|
|
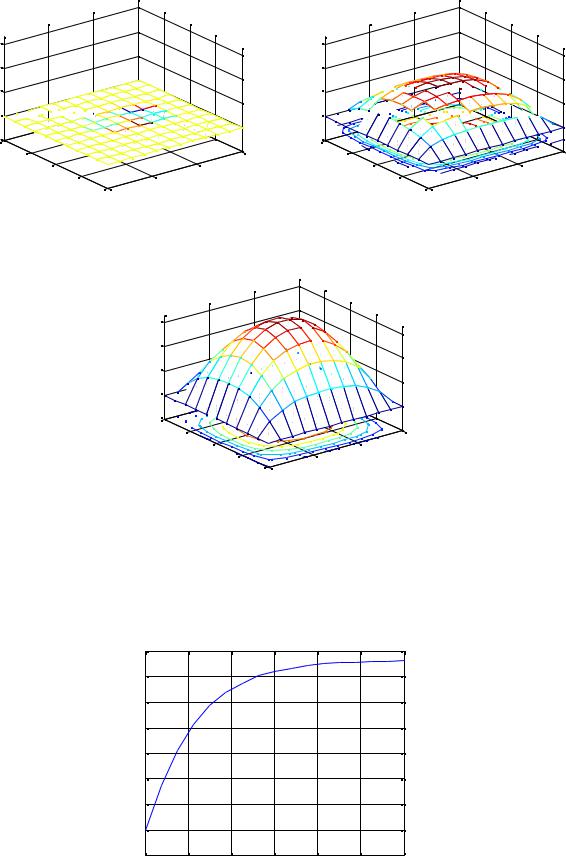
Рисунок 13.
Зависимость температуры от времени в точке с координатами (0,1 ; 0,15). 25
