
_books_met_files_fund_radio_el
.pdf
21
|
|
|
|
|
S t t0 |
e j tdt e j t0 , |
|
||
|
|
|
|
|
|
S 1 e j t0 |
, |
(2.35) |
|
S 1. (см. рис. 2.13)
S |
По свойству преобразования Фурье о смещенном |
|||||
1 |
|
во времени сигнале можно представить -функцию: |
||||
|
|
|
1 |
|
1 |
|
|
|
t |
S ej td или t |
e j td . |
||
|
|
2 |
2 |
|||
|
|
|
|
|||
|
|
|
|
|||
0
Рис. 2.13
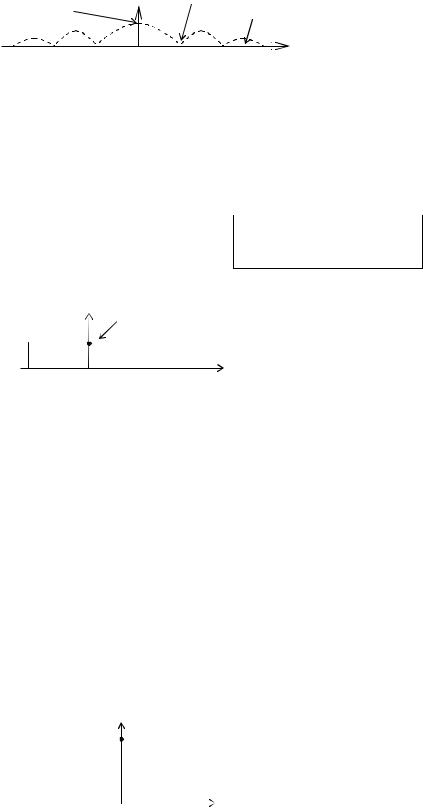
Качественно можно эту формулу обосновать следующим образом: воспользуемся формулой Эйлера
ej t cos t jsin t.
Мы можем представить приведенный выше интеграл в виде суммы большого числа синусоид и косинусоид различных частот.
cos t |
sin t |
t |
t |
a) б) Рис. 2.14
Как видно из рисунка 2.14-б, в любой момент времени t, отличный от t=0, число положительных составляющих sin t будет равно числу отрицательных составляющих и, следовательно, их вклады могут привести к разрушительной интерференции или полной взаимной компенсации. При t=0, однако, все косинусоидальные составляющие равны +1; их вклад суммируется, создавая в начале координат бесконечно большой пик (см. рис. 2-14-а).
2) Спектральная плотность постоянного во времени сигнала.
U t E const,
|
1 |
|
|
|||
S Ee j tdt 2 E |
e j tdt 2 E , |
|
||||
2 |
|
|||||
|
|
|
||||
|
|
|||||
|
|
S 2 E |
. |
(2.36) |
||
U |
|
S |
|
|||
|
|
|
|
|
|
|
0 |
t |
0 |
|
Рис. 2.15 |
|
||
|
|
|

22
3) Спектральная |
|
плотность |
комплексного |
|
экспоненциального |
сигнала |
|||||
U t exp j 0t может быть определена следующим образом: |
|
||||||||||
S U t |
e j tdt ej 0te j tdt 2 |
1 |
|
e j 0 dt 2 0 , |
|||||||
|
|
|
|||||||||
|
|
|
|
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Спектр несимметричен |
S 2 0 |
. |
|
|
(2.37) |
||||||
относительно =0. |
|
|
|
||||||||
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
0 |
0 |
|
|
|
|
|
|
||||
|
Рис. 2.16 |
|
|
|
|
|
|
||||
4) Спектральную |
|
|
плотность |
гармонического |
сигнала |
||||||
U t cos 0t |
1 |
ej 0t e j 0t |
определим |
воспользовавшись линейностью |
|||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
преобразования Фурье и спектральной плотностью комплексной экспоненты.
Спектр симметричен |
S 0 0 |
. |
(2.38) |
|||||
относительно 0. |
|
S |
|
|
|
|||
U(t) |
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
0 |
- 0 0 |
|
||||||
|
0 |
|||||||
|
Рис. 2.17 |
|
|
|
|
|
|
|
2.5. Спектральная плотность периодического сигнала
Найдем спектральную плотность периодического U(t) сигнала с периодом
T — U(t)=U(t T). |
|
|
|
|
Фурье для периодического сигнала U(t) |
||||||||
Экспоненциальный |
|
ряд |
|||||||||||
|
|
|
где 1 |
|
2 — |
основная частота, |
n=0, 1, 2,.... Коэффициенты |
||||||
U t Cnejn 1t , |
|||||||||||||
n |
|
|
|
T |
|
|
|
|
|
|
|||
|
1 |
|
T /2 |
|
|
|
|
|
|
|
|
|
|
Cn |
|
U t e jn 1tdt . |
|
|
|
|
|
|
|
|
|||
T |
|
|
|
|
|
|
|
|
|||||
|
|
|
T /2 |
|
|
|
|
|
|
|
|
|
|
Но |
при |
|
этом, |
по |
определению, |
спектральная |
плотность |
||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
||
S U t e j tdt Cnejn 1t e j tdt 2 Cn |
|
e j n 1 |
tdt |
||||||||||
2 |
|||||||||||||
|
|
|
n |
|
n |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
2 Cn n 1 , |
|
|
|
|
|
|
|
|
|||||
n |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т.е. |
S 2 Cn n 1 |
. |
|
|
|
(2.39) |
||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
23
Таким образом, спектральная плотность периодического сигнала представляется на оси частот последовательностью — функций, существующих
на частотах =n 1 |
|
(n=0, 1, 2,...), |
с интенсивностью (площадью) 2 Сn, |
||||||||||||||||||||||||||
определяемой видом одиночного сигнала U(t). |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
22 СС00 |
|
|
|
S |
2 / u |
n |
На |
рис. |
2.18 |
показан |
спектр |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
периодической |
|
последовательности |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
прямоугольных |
видеоимпульсов |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
- 10 1 |
|
|
|
|
|
|
|
|
(пунктиром |
– |
спектр |
одиночного |
|||||||||
|
|
|
|
|
|
|
Рис.2.18 |
|
|
|
|
|
|
|
|
видеоимпульса) |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
последовательность |
|
|
||||||||||||
Если |
сигнал – это |
|
|
периодическая |
импульсов, то |
||||||||||||||||||||||||
|
|
|
1 |
T /2 |
t e jn 1tdt |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Cn |
T /2 |
. |
|
Отсюда |
(из |
2.39) |
спектр |
периодической |
|||||||||||||||||||||
T |
T |
||||||||||||||||||||||||||||
последовательности импульсов равен |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S 2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 . |
|
|
|
(2.40) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T n |
|
|
|
|
|
|
||
Этот спектр изображен на рис. 2.19.
S 2 /T









 -2
-2
Рис. 2.19
3. Дискретизация сигнала
При переходе от аналогового сигнала к цифровому осуществляются три специфических преобразования: дискретизация по времени, квантование по уровню и кодирование. Под дискретизацией понимают процесс замены непрерывного сигнала дискретной последовательностью отсчетов через интервал
t.
3.1. Ортогональные сигналы с ограниченным спектром
Рассмотрим идеальный низкочастотный (НЧ) сигнал, т.е. сигнал U(t), имеющий постоянную вещественную спектральную плотность в диапазоне - в, + в.
|
|
Su |
|
|
0, |
|
в, |
|
|
|
|
|
|
|
|
|
|
|
|
S0 |
|
|
Su S0 |
, |
в в, |
(3.1) |
|
|
|
|
|
|
|
в. |
|
|
|
|
|
|
0, |
|
|
|
- |
|
|
|
в |
|
|
|
|
в |
0 |
+ |
|
|
|
Рис. 3.1

24
|
U t |
1 |
|
j t |
d |
S0 |
в |
j t |
d ; |
U |
2 |
Su e |
|
2 |
e |
|
|||
|
|
|
|
|
|
|
|
|
|
S0 в/ |
|
|
|
|
|
|
в |
|
|
|
т.к. |
|
в |
|
|
|
|
|
то |
|
|
ej td 2sin вt , |
|
|
|||||
|
|
|
в |
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U t |
S0 в |
|
-2 / в |
- / в 0 |
/ в |
t |
|
||
|
||||||
2 / в |
|
|
Рис. 3.2
Если НЧ сигнал запаздывает на t, то V t S0 в
sin вt .
вt
sin в t t ,в t t
тогда по свойству преобразования Фурье задержанного сигнала имеем
0, в,
Sv S0e j t , в в,0, в.
(3.2)
(3.2’)
(3.1’)
Рассмотрим эти два идеальных НЧ сигнала U t и V t . Оба имеют одинаковые параметры S0 и в, однако сигнал V t запаздывает по отношению к
сигналу U t на время t, так, что его спектральная плотность Sv Su e j t . Скалярное произведение этих сигналов, полученное по обобщенной формуле
Рэлея (2.34), UV |
1 |
SuSv , |
UV |
1 |
|
* |
S02 |
в |
j t |
|
S02 в sin в t |
|
||
|
|
SuSv d |
|
вe |
|
d |
|
|
|
. |
||||
2 |
2 |
2 |
|
|
в t |
|||||||||
Обозначим t=tk.
Скалярное произведение обращается в нуль, и эти сигналы оказываются ортогональными, если временной сдвиг между ними удовлетворяет условию
вtk k k 1, 2,... , t tk k в .
Минимально возможный сдвиг, приводящий к ортогонализации, получается при k= 1. Причем, максимум одного сигнала всегда совпадает с нулем другого.
|
t |
|
|
|
1 |
. |
(3.3) |
|
|
|
|
|
|||||
U |
1 |
|
в |
|
2F |
|
||
|
V |
|
|
|
в |
|
||
0 |
t2 |
t3 |
t |
|
 t1= / в
t1= / в
Рис. 3.3

25
Важно — удалось не просто добиться ортогональности двух сигналов. Указан путь построения бесконечного ортогонального базиса, который может служить координатной системой для разложения произвольного сигнала со спектром, ограниченным частотой в.
3.2. Теорема Котельникова для сигнала с ограниченным спектром
Для создания ортонормированного базиса достаточно рассмотреть функцию
l0 |
t A |
sin вt |
, создающую ортогональный базис и определить амплитуду А, |
|
вt |
||||
|
|
|
чтобы норма была единична. По определению, энергия сигнала равна квадрату
|
|
|
|
|
|
|
2 |
|
A2 |
|
|
t |
|
A2 |
|
A2 |
|
нормы E |
|
|
|
l02dt |
sin2 |
dt |
в |
||||||||||
|
|
l0 |
|
|
|
|
|
|
в |
|
|
. |
|||||
|
|
|
|
|
|
2 |
|
2 |
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
в |
|
t |
|
|
|
в |
|
в |
Итак, |
функция l0(t) будет ортонормированной, т.е. (Е=1), если A |
в |
. |
|||||||||||
Бесконечная совокупность функций |
|
|
|
|
|
|||||||||
|
|
sin в t tk |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
, |
|
|||
|
|
|
|
|
|
|
lk t, в |
в |
(3.4) |
|||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
1 |
|
|
|
в t tk |
|
|
|||
где t |
k |
k |
k |
, образуют базис Котельникова в линейном пространстве НЧ |
||||||||||
|
в |
2F |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
в |
|
|
|
|
|
|
|
||
сигналов со спектрами, ограниченными сверху значением в . Отдельная функция
lk называется отсчетной функцией базиса Котельникова.
Если U t — произвольный сигнал, спектральная плотность которого отлична от нуля лишь в полосе частот в в , то его можно разложить в обобщенный ряд Фурье по базису Котельникова
U t Cklk t, в .
k
Коэффициентами ряда служат, как известно, скалярные произведения разлагаемого сигнала и k-ой отсчетной функции Ck U t lk . По обобщенной
формуле Рэлея (2.34)Ck |
1 |
Su Slk . Т.е. |
|
|
|
|
|
|||||||||||||||
2 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Ck |
|
|
Su |
Slk d |
|
|
(3.5) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||
Коэффициенты Ck |
находим по аналогии с выражениями (3.2’) и (3.1’) т.к. |
|||||||||||||||||||||
|
|
|
sin в t tk |
|
|
|
|
k |
|
|
|
|
|
|
||||||||
lk t |
в |
|
|
tk |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
, где |
|
|
, |
|
|
|
|
|
|
|||||
|
|
в |
t t |
k |
|
|
|
2F |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
|||
то |
для |
k |
|
- ой |
|
отсчетной функции |
имеем Slk |
|
|
|
exp j tk (здесь, в |
|||||||||||
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
||
соответствии с теоремой запаздывания, экспонента показывает сдвиг отсчетной

26
функции |
во |
|
|
|
|
|
времени). |
|
|
|
|
|
Тогда |
|
|
из |
(3.5) |
имеем |
||||||
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ck |
|
|
Su |
|
|
exp j tk d |
|
|
|
|
|
|
|
Su exp j tk d . |
|
|||||||||
2 |
в |
|
|
в |
2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|||
Т.к. tk |
k |
— k-ая отсчетная точка, то фигурная скобка есть не что иное, как U tk . |
||||||||||||||||||||||
в |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U tk . Следовательно, т.к. |
|
|
||||||||||||
Таким образом, Ck |
|
|
U t Cklk t , используя (3.4), |
|||||||||||||||||||||
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
k |
|
|
||
имеем ряд Котельникова |
|
|
|
|
|
sin в t tk . |
|
(3.6) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
U t Uk |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
в t tk |
|
|
|
|
|||||
Теорема: Произвольный сигнал, спектр которого не содержит частот выше Fв (Гц), может быть полностью восстановлен, если известны отсчетные значения этого сигнала, взятые через равные промежутки времени t=1/2 Fв (c).
3.3. Спектр дискретизированного сигнала
Дискретизированный сигнал можно рассматривать как результат умножения первоначального непрерывного сигнала U(t) на сигнал i(t), состоящий из бесконечного числа единичных -импульсов
i t t nTд ,
n
где Tд – период дискретизации.
Эта операция дает дискретизированный сигнал
Ui t U t i t U nTд t Tд .
n
Воспользовавшись теоремой о свертке
S Su g Si g dg ,
где Su(...)– преобразование Фурье от функции U(t), Si(...)– преобразование Фурье от функции i(t).
Преобразование Фурье ряда, состоящего из -импульсов, как было показано выше (см. (2.38)),
Si g 2Tд n g n 1 2Tд n g 2Tдn ,
отсюда
|
2 |
|
|
2 n |
|
2 |
|
|
|
2 n |
|
|
|
|
|
|
|
|
|
||||
S Su g T |
g |
T |
dg |
T |
Su |
T |
. |
||||
|
д |
n |
|
д |
|
д |
n |
|
|
д |
|
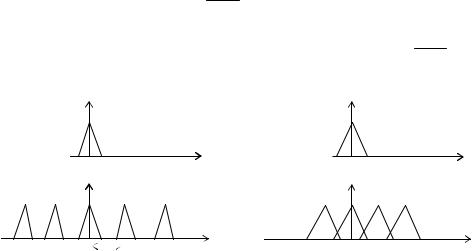
Следовательно, дискретизированный, или импульсно-модулированный
сигнал Ui(t) имеет периодическое с периодом Fд 1 преобразование Фурье S( ),
Tд
27
интенсивность которого уменьшается в Tд раз. Если спектр Su( ) при F>Fв, обращается в ноль и Tд 21Fв или Fд 2Fв, то S( ) является просто периодически
повторяемой функцией Su( ) (рис.3.5). Если Tд 21Fв , то имеет место эффект наложения частот (рис. 3.6).
|
|
Su |
|
|
Su |
|
|
|
в |
|
|
|
|
0 |
|
0 |
||||
|
|
|
|
|
S |
|
|
|
S |
|
|
|
|
0 |
|
д |
|
0 |
||
|
|
|
|
|||
Рис. 3.5 |
|
|
Рис. 3.6 |
|
||
4. Модулированные сигналы и их спектры
Для передачи информации на расстояние применяются сигналы, эффективно излучаемые с помощью антенных устройств и способные распространяться в виде свободных радиоволн в среде, разделяющей источник информации от получателя информации.
Такими сигналами являются высокочастотные колебания. Передаваемая информация должна быть как-то заложена в высокочастотное колебание,
называемое несущим. Частота этого колебания выбирается в зависимости от расстояния, условий распространения радиоволн и других факторов. Но в любом
случае частота 0 должна быть велика по сравнению с наивысшей частотой m спектра передаваемого сообщения. Любой сигнал можно, поэтому, трактовать как «узкополосный» процесс даже при передаче широкополосных сообщений.
4.1. Сигналы с амплитудной модуляцией (АМ)
Физически процесс управления колебанием и называется модуляцией. Чаще всего в качестве несущего используют простое гармоническое колебание
V=Ucos( t+ ).
Если переменной оказывается амплитуда сигнала U(t), а остальные
параметры и |
неизменны, имеет место амплитудная |
модуляция несущего |
колебания |
uАМ U t cos 0t 0 , |
(4.1) |
|
где U(t) — огибающая, cos( 0t+ 0) — высокочастотное заполнение.

28
Причем при двухполосной передаче сигнал можно представить
U t U0 1 mX t , (4.2)
где m — коэффициент модуляции, X(t) — передаваемое сообщение, U0 — амплитуда несущей в отсутствии модуляции.
Рассмотрим простейший случай однотональной модуляции.
Однотональная амплитудная модуляция – модуляция гармоническим колебанием частотой
UАМ t U0 1 m cos t cos 0t 0
U |
0 |
cos t |
|
U0m |
cos |
0 |
t |
0 |
|
(4.3) |
|
|
|||||||||||
|
0 |
0 |
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
U20mcos 0 t 0 .
Отсюда следует, что однотональная модуляция симметрична относительно
несущего колебания.
U
U0
0

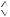 U SАМ
U SАМ
2 /
2 /
Рис. 4.1
Из рис. 4.1 видно,
|
|
t |
|
|
U0 |
|
||
|
|
U0m/2 |
|
U0m/2 |
|
|||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
0 |
0- |
0 0+ |
||||
|
|
|
||||||
|
U=mU0 |
|
Рис. 4.2 |
|
||||
|
|
|
||||||
|
|
U . При |
|
|
||||
|
|
|
|
|||||
что m |
неискаженной модуляции (m 1) |
|||||||
|
|
U0 |
|
|
|
|
|
|
амплитуда колебания изменяется в пределах Umin=U0(1-m) до максимальной
Umax=U0(1+m).
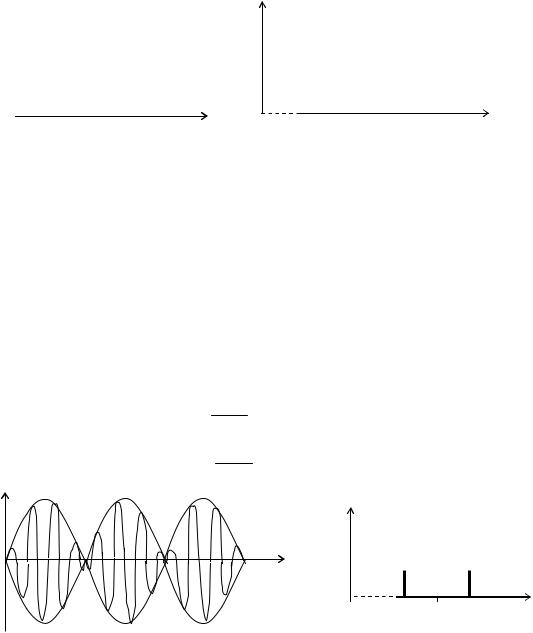
На практике однотональные АМ сигналы используются редко. Гораздо более реален случай, когда модулирующий НЧ сигнал имеет сложный спектральный состав. Математической моделью такого НЧ сигнала может быть, например, тригонометрическая сумма
|
|
|
N |
|
|
|
|
|
X t i cos it i . |
(4.4) |
|
|
|
i |
i 1 |
|
|
Здесь |
частоты |
образуют |
упорядоченную |
возрастающую |
|
последовательность 1< 2<...< N, в то время как амплитуды i и начальные фазыi произвольны.
Подставив (4.4) в (4.1), получим
u t U |
|
|
|
N |
m |
cos |
|
cos |
t . |
0 |
1 |
|
t |
||||||
|
|
|
i |
i |
i |
0 |
|
||
|
|
|
|
i 1 |
|
|
|
|
|
Введем совокупность парциальных коэффициентов модуляции
mi m i
и запишем аналитическое выражение многотонального АМ-сигнала
29
|
|
|
|
|
|
|
u t U |
|
|
|
N |
m cos |
t |
|
|
|
|
|
|
t . |
(4.5) |
||||||||||||
|
|
|
|
|
|
|
|
1 |
|
cos |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
i |
i |
|
|
|
|
i |
|
|
|
|
0 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Спектральное разложение получается аналогично (4.3): |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
U |
m |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
u t U0 cos 0t |
|
|
0 |
|
i |
cos 0 |
|
i t i |
|
||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
N |
U |
m |
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
cos 0 |
i t i . |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
i |
|
|
|
(4.6) |
||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
i 1 |
|
|
SАМ |
|
|
|
|
|
|
|
|
|
Sv |
|
|
|
|
|
|
|
||||
Sx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
0 |
1 |
2 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Рис. 4.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.4 |
|
|
|
|
|||||||||||
Итак, спектр сложномодулированного АМ колебания помимо несущего содержит группы верхних и нижних боковых колебаний.
4.1.1. Балансная амплитудная модуляция (подавленная несущая)
Значительная доля мощности обычного АМ сигнала сосредоточена в несущем колебании. Для более эффективного использования можно формировать АМ сигнал с подавленной несущей:
VБМ |
U0mcos t cos 0t |
|||
|
U0mcos 0 |
t |
(4.7) |
|
|
2 |
|
|
|
|
U0mcos 0 |
t . |
|
|
VБМ |
2 |
SБМ |
|
|
|
|
|
||
|
|
|
|
|
0 |
t |
|
U0m/2 |
U0m/2 |
|
|
|
||
|
|
|
|
|
|
|
0 |
0- |
0 0+ |
Рис. 4.5
Итак, здесь имеет место перемножение двух сигналов – модулирующего и несущего. Колебания вида (4.7) с физической точки зрения являются биениями двух гармонических сигналов с одинаковыми амплитудами U0m/2 и частотами, равными верхней боковой и нижней боковой.

30
Здесь при переходе огибающей биений через ноль, фаза высокочастотного заполнения меняется скачком на 180 , поскольку функция cos( t+ ) имеет разные знаки слева и справа от нуля. В результате на выходе добротного контура не будет сигнала на частоте резонанса 0.
4.1.2. Однополосная амплитудная модуляция (ОБП)
V |
t U |
0 |
cos |
t |
U0m |
cos |
0 |
t . |
(4.8) |
|
|||||||||
ОБП |
|
0 |
2 |
|
|
|
|||
SОБП |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
0 |
0+ |
||||
|
||||||
Рис. 4.6
Чтобы найти огибающую сигнала, проведя преобразование, имеем:
V |
|
|
|
t U |
0 |
cos |
t |
U0m |
cos t cos |
t |
|
|
||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
ОБП |
|
|
|
|
0 |
|
|
|
|
2 |
|
|
|
|
|
|
0 |
|
|
|
||||
|
|
|
U0m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
sin t sin 0t |
|
|
|
|
|
|
(4.8’) |
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
2 |
m |
|
|
|
|
|
|
|
|
|
|
U |
|
m |
|
|
|
|
|
||
U |
|
|
|
|
|
cos |
t |
0 |
sin t sin |
t . |
||||||||||||||
0 |
1 |
|
|
cos t |
|
|
||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
0 |
|
|
|
|
2 |
|
|
0 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
В последнем выражении оба члена представляют собой произведение двух |
||||||||||||||||||||||||
функций – медленной |
(частота ) и |
быстрой (частота |
Напомним, |
что |
||||||||||||||||||||
|
|
|
|
A |
|
; tg b . |
|
|
||||||||||||||||
asin t bcos t Asin t , |
|
где |
|
a2 b2 |
Принимая |
во |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
внимание, что “быстрые” сомножители в выражении (4.8’) находятся между собой в квадратуре, вычисляем медленно изменяющуюся огибающую:
U t U |
|
|
|
m |
|
2 |
m2 |
sin |
2 |
t |
0 |
1 |
|
cos t |
|
|
|
||||
|
|
|
2 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
(4.9) |
||
|
|
|
|
|
|
|
|
|
|
U0 
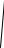 1 mcos t m42 ,
1 mcos t m42 ,
ав АМ колебании огибающая равна U0 1 mcos t . Спектр ОБП сигнала и огибающая приведены на рис. 4.7.
SОБП |
|
|
|
|
|
U/U0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1,5 |
|
АМ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m=1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
ОБП |
|
|
|
|
|
||||
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
t |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
0 0 |
0+ 0+ |
0+ |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||||||||||
Рис. 4.7
