Глава 2 Математическая модель

Имеется N взаимодействующих материальных точек(частиц), которые находятся под воздействием некоторого внешнего силового поля. Уравнения движения имеют вид

(1)

где и – векторы положения и скорости k-ой частицы,

(2)

m-масса частицы. Φ(r) и Ψ(r,v) описывают консервативную и неконсервативную составляющую взаимодействия между частицами, и 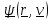описывают внешнее консервативное и неконсервативное силовое поле. Неконсервативная составляющая описывает внутреннюю диссипацию системы, в данной работе она не рассматривается. Рассмотрим консервативную составляющую

(3)

где f(r) – скалярная сила взаимодействия между частицами, П(r) – потенциал взаимодействия. Величина Ф(r) является важнейшим силовым фактором, во многих задачах все остальные силовые факторы уравнения (1) отбрасываются.

Моделирование методом молекулярной динамики с математической точки зрения представляет собой решение задачи Коши для уравнений (1). Начальные условия включат себя координаты и скорости каждой частицы. Генерация начальных условий – отдельная нетривиальная задача, так как мы должны учесть строение вещества, расположение частиц, их скорости, макро- и микропараметры, а это все существенно влияет на свойства материала и результаты вычислений.

На рис. 1 представлены одни из возможных начальных параметров

Рис. 1

В простейшем случае, для моделирования метода молекулярной динамики может быть использован потенциал Ленарда-Джонса(потенциал 6-12), который записывается в следующем виде

где r – расстояние между центрами частиц, ε – глубина потенциальной ямы, σ – расстояние, на котором энергия взаимодействия становится равной нулю. Характерный вид данного потенциала представлен на рис. 2.

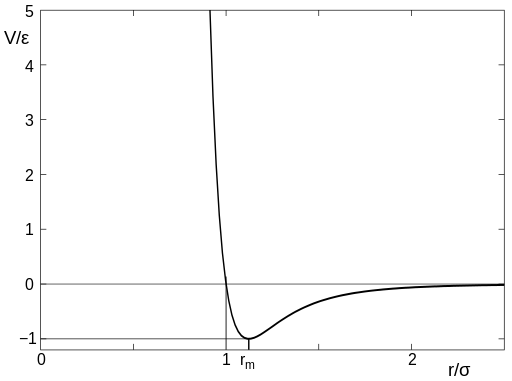
Рис.2

При больших r молекулы притягиваются, что соответствует члену со степенью 6 в формуле. Эту зависимость можно обосновать теоретически, и обусловлена она силами Ван-дер-Ваальса(диполь-дипольное индуцированное взаимодействие). На малых же расстояниях молекулы отталкиваются из-за обменного взаимодействия(при перекрытии электронных облаков молекулы начинают сильно отталкиваться), чему соответствует член со степенью 12 в формуле.

Потенциал Ленарда-Джонса описывает парное взаимодействие между молекулами, поэтому он не подходит для моделирования материалов с большой плотностью, т.к. в этом случае, строго говоря, взаимодействие уже не является парным.

В дипломной работе используется COMB(charge-optimized many-body)-потенциал. Его применение обусловлено тем, что многие вещества содержат разнородные связи, например: металлы и оксиды металлов, полупроводников и оксиды металлов и оксиды металлов и газообразные молекулы, и др. В связи с этим, National Science Foundation (NSF) и Department of Energy (DOE) совместно с профессором Simon Phillpot (University of Florida) разработали COMB-потенциал. Этот потенциал учитывает динамический перенос заряда между атомами. На данный момент, ведется работа по параметризации третьего поколения COMB-потенциала, которое будет применимо для металлических и металл-оксидных систем. В настоящее время, параметризация проведена для многих веществ, в частности для ZnO, и данный потенциал может быть использован в LAMMPS.Его вид

где - собственная энергияi-го атом, - взаимодействиеi-го и j-го атомов, - описывает кулоновские взаимодействия,- поляризация,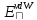- взаимодействия Ван-дер-Ваальса,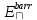- барьерная функция,– корректировки углов.