
Упражнения
Исследовать сходимость следующих несобственных интегралов:
1.
![]() 2.
2.![]() 3.
3.![]()
4.![]() 5.
5.![]() 6.
6.![]()
7.
 8.
8.![]() 9.
9.![]()
10.
![]() 11.
11.![]() 12.
12.![]()
13.
![]() 14.
14.![]() 15.
15.
16.
![]() 17.
17.![]() 18.
18.![]()
19.
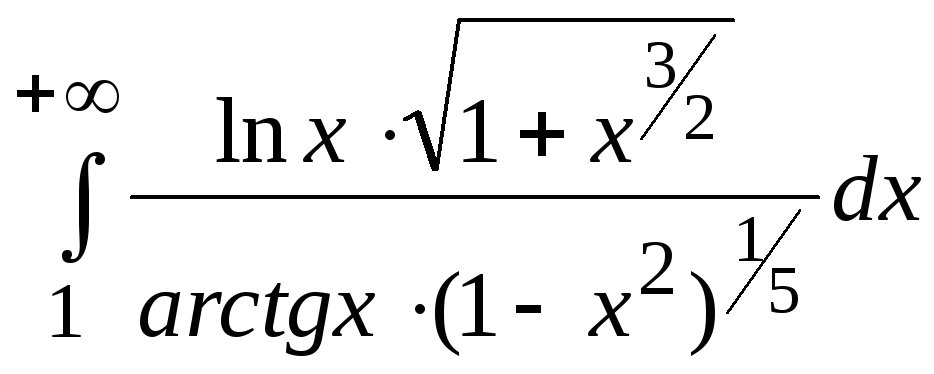 20.
20.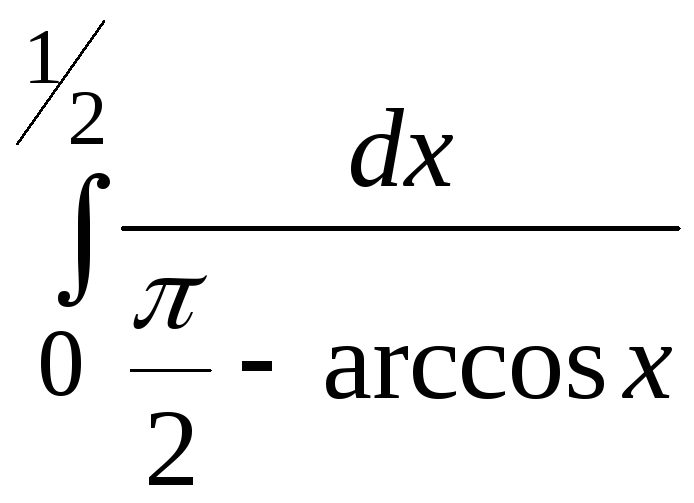 .
.
3 Несобственные интегралы от функций, меняющих знак
Если
![]() ,
то функция
,
то функция![]() называется абсолютно интегрируемой
на
называется абсолютно интегрируемой
на![]() в несобственном смысле, а несобственный
интеграл
в несобственном смысле, а несобственный
интеграл![]() --
абсолютно сходящимся.
--
абсолютно сходящимся.
Если
![]() ,
а
,
а![]() ,
то говорят, что несобственный интеграл
,
то говорят, что несобственный интеграл![]() сходится условно.
сходится условно.
3.1 Признак Вейерштрасса (признак абсолютной сходимости).
Если
![]() ,
то
,
то![]() и при этом
и при этом![]() .
.
3.2 Признак Дирихле.
Пусть
![]() и
и
а)
![]() -- локально интегрируемая функция на
-- локально интегрируемая функция на![]() и
и
![]()
![]() ;
;
б)
![]() --
монотонная на
--
монотонная на![]() функция;
функция;
в)
![]() .
.
Тогда
несобственный интеграл
![]() сходится.
сходится.
3.3 Признак Абеля.
Пусть
![]() ,
,![]() --
монотонная и ограниченная на
--
монотонная и ограниченная на![]() функция. Тогда
функция. Тогда![]() сходится.
сходится.
Рассмотрим несколько примеров, в которых применяются приведенные выше признаки для исследования на абсолютную и условную сходимость несобственные интегралы.
Исследовать на абсолютную и условную сходимость следующие несобственные интегралы.
Пример
1.
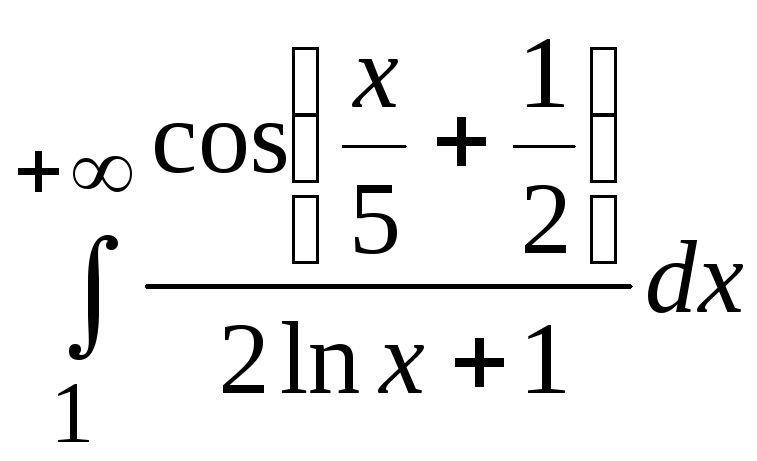 .
.
Функция
![]() ,
следовательно,
,
следовательно,![]() --
единственная особая точка. Функция не
сохраняет знак на
--
единственная особая точка. Функция не
сохраняет знак на![]() ,
так как
,
так как![]() и поэтому
и поэтому![]() меняет знак.
меняет знак.
Исследуем рассматриваемый интеграл на условную сходимость. Для этого рассмотрим
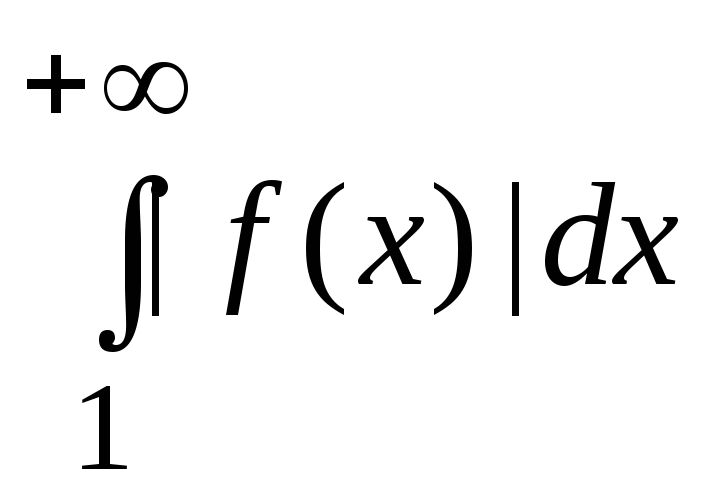 .
.
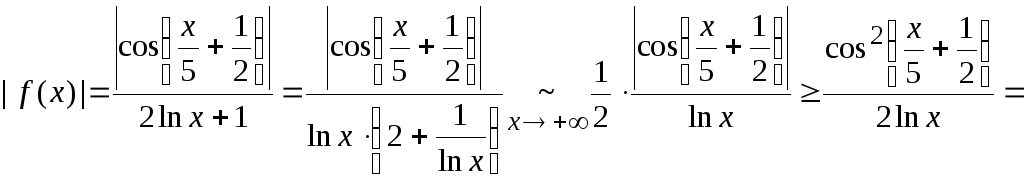
 .
.
Обозначим
через
![]() и
и![]() .
.
Так
как
![]() и
и![]() ,
причем
,
причем![]() расходится, то по признаку сравнения
в непредельной форме расходится
расходится, то по признаку сравнения
в непредельной форме расходится![]() .
.
Покажем,
что
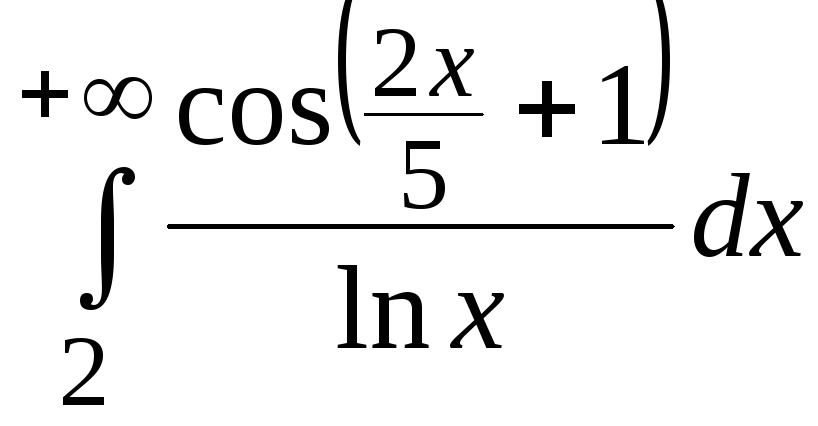 сходится, используя для этого признак
Дирихле:
сходится, используя для этого признак
Дирихле:
а)
![]()
![]()
![]() ;
;
б)
![]() убывает на
убывает на![]() ;
;
в)
![]() .
.
Итак:
![]() ,
где
,
где![]() -
расходится, а
-
расходится, а![]() -
сходится. Тогда
-
сходится. Тогда![]() -
расходится. Следовательно, по признаку
сравнения в непредельной форме расходится
-
расходится. Следовательно, по признаку
сравнения в непредельной форме расходится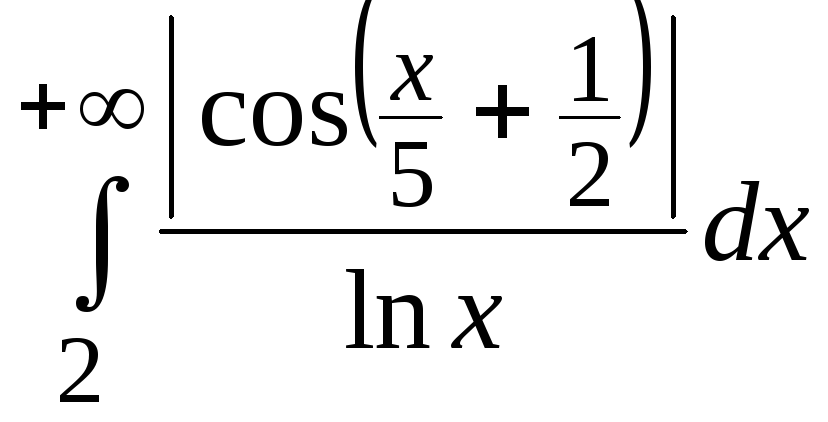 .
.
Отсюда
следует, что
![]() расходится по признаку сравнения в
пре-
расходится по признаку сравнения в
пре-
дельной
форме, а, значит, расходится и
![]() .
.
2.
Исследуем сходимость
![]() ,
используя для этого признак Дирихле.
,
используя для этого признак Дирихле.
Пусть
![]() ,
а
,
а![]() .
.
Тогда
а)
![]() --
локально интегрируема на
--
локально интегрируема на![]() и
и![]()
![]() ;
;
б)
![]() убывает на
убывает на![]() ;
;
в)
![]() .
.
Следовательно,
![]() сходится по признаку Дирихле, а так как
сходится по признаку Дирихле, а так как![]() расходится, то исходный интеграл сходится
условно.
расходится, то исходный интеграл сходится
условно.
Пример
2.![]() .
.
Функция
![]() ,
следовательно,
,
следовательно,![]() --
единственная особая точка;
--
единственная особая точка;![]() не сохраняет знак на
не сохраняет знак на![]() .
Поэтому исследуем сначала интеграл на
абсолютную сходимость.
.
Поэтому исследуем сначала интеграл на
абсолютную сходимость.
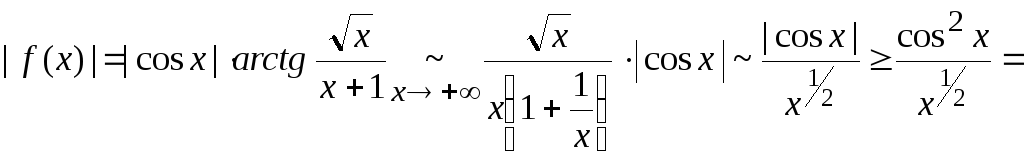
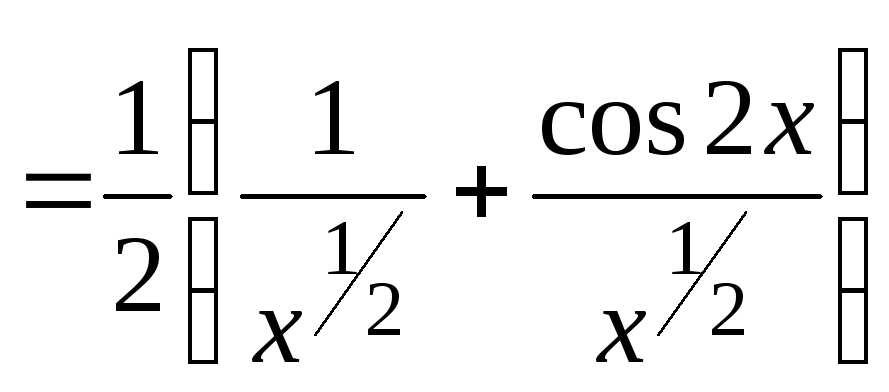 .
.
![]() расходится,
так как
расходится,
так как
![]() ,
а
,
а![]() сходится по признаку Дирихле. Обоснуем
последнее:
сходится по признаку Дирихле. Обоснуем
последнее:
а)
![]()
![]() ;
;
б)
функция
![]() убывает на
убывает на![]() ;
;
в)
![]() .
.
Итак,
имеем:
![]() , где
, где расходится как сумма расходящегося
и сходящегося интеграла. Следовательно,
по признаку сравнения в непредельной
форме расходится
расходится как сумма расходящегося
и сходящегося интеграла. Следовательно,
по признаку сравнения в непредельной
форме расходится![]() .
Тогда по признаку сравнения в предельной
форме расходится
.
Тогда по признаку сравнения в предельной
форме расходится![]() ,
а, значит, расходится и
,
а, значит, расходится и![]() .
Значит, исходный интеграл не имеет
абсолютной сходимости.
.
Значит, исходный интеграл не имеет
абсолютной сходимости.
2.
Исследуем
![]() .
.
Пусть
![]() .
Тогда
.
Тогда
a)
![]() --
локально интегрируема на
--
локально интегрируема на
![]() и
и![]()
![]() ;
;
б)
![]() является суперпозицией двух функций:
является суперпозицией двух функций:![]() --
монотонно возрастающей и
--
монотонно возрастающей и![]() .
Исследуем последнюю на монотонность
при помощи производной:
.
Исследуем последнюю на монотонность
при помощи производной:
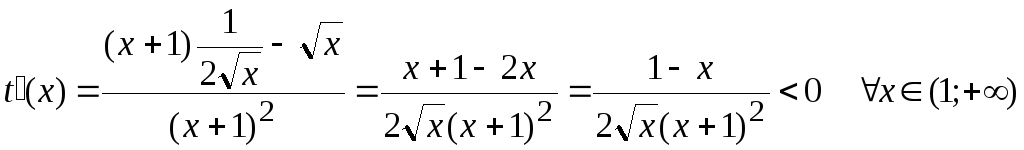 ;
;
в)
 .
.
Следовательно,
![]() сходится по признаку Дирихле, а, значит,
сходится по признаку Дирихле, а, значит,![]() =
=![]() +
+![]() сходится как сумма
интегралов Римана и
сходится как сумма
интегралов Римана и
сходящегося
несобственного интеграла. И так как
абсолютной сходимости нет, то
![]() сходится условно.
сходится условно.
Пример
3.
 .
.
Функция
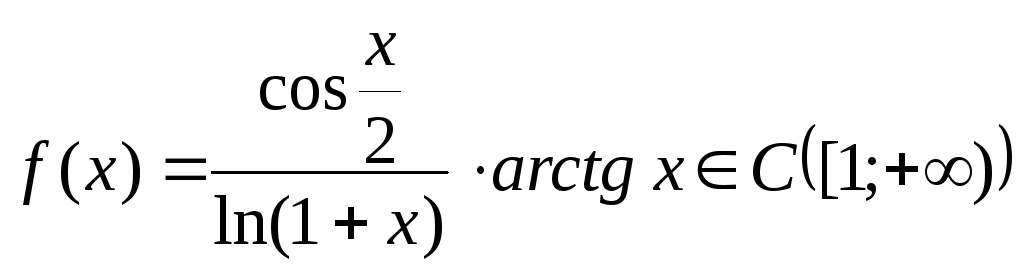 ,
следовательно,
,
следовательно,![]() --единственная
особая точка. Функция
--единственная
особая точка. Функция![]() не сохраняет знак на
не сохраняет знак на![]() .
.
1.
Исследуем
![]() .
.
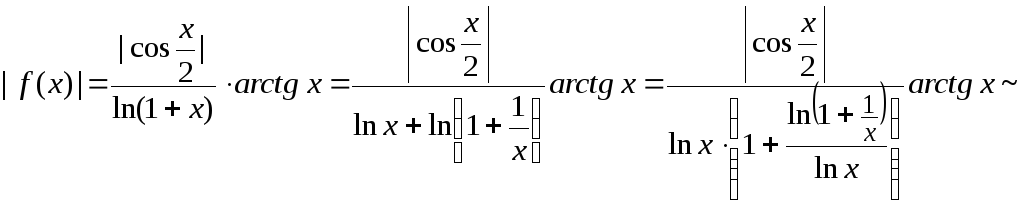
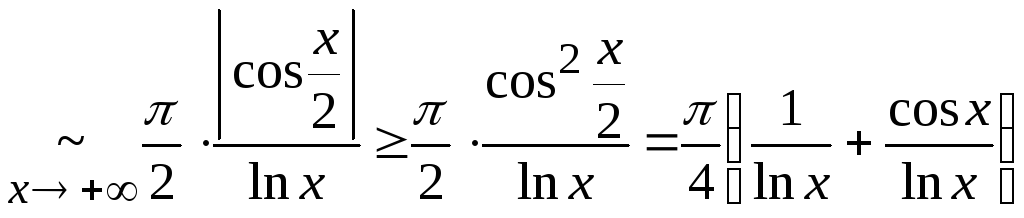 .
.
Так
как
![]() ,
то по признаку сравнения в непредельной
форме
,
то по признаку сравнения в непредельной
форме![]() расходится, а
расходится, а![]() сходится по признаку Дирихле. Покажем
последнее:
сходится по признаку Дирихле. Покажем
последнее:
а)
![]() ;
;
б)
функция
![]() монотонно убывает на
монотонно убывает на![]() ;
;
в)
![]() .
.
Итак,
![]() ,
где
,
где![]() ,
расходится как сумма расходящегося
и сходящегося интегралов. Следовательно,
по признаку сравнения в непредельной
форме
,
расходится как сумма расходящегося
и сходящегося интегралов. Следовательно,
по признаку сравнения в непредельной
форме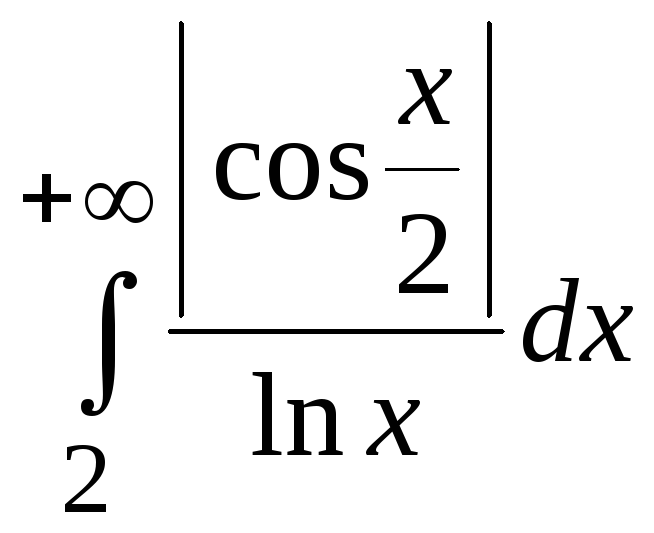 расходится. Тогда
по признаку сравнения в предельной
форме расходится
расходится. Тогда
по признаку сравнения в предельной
форме расходится
![]() ,
а, значит и
,
а, значит и![]() расходится.
расходится.
2.
Исследуем
![]() .
.
Пусть
![]() .
.
![]() сходится
по признаку Дирихле, так как
сходится
по признаку Дирихле, так как
а)
![]() ;
;
б)
![]() убывает на
убывает на![]() ;
;
в)
![]() .
.
Функция
![]() возрастает на
возрастает на![]() и ограничена, так как
и ограничена, так как![]() .
.
Следовательно,
![]() сходится по признаку Абеля, и так как
абсолютной сходимости нет, то сходится
условно.
сходится по признаку Абеля, и так как
абсолютной сходимости нет, то сходится
условно.
Пример
4.![]() .
.
Функция
![]() ,
поэтому
,
поэтому![]() --
единственная особая точка; функция не
сохраняет знак на
--
единственная особая точка; функция не
сохраняет знак на![]() .
.
1.
Исследуем сходимость
![]() .
.
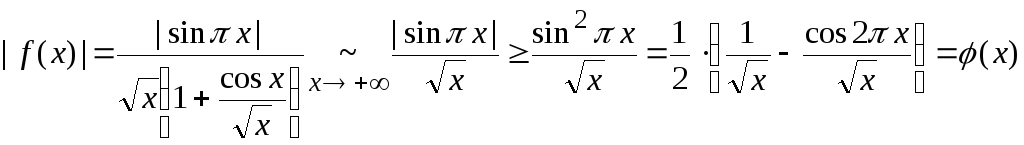 .
.
Очевидно,
что
![]() расходится, так как это сумма расходящегося
ин-
расходится, так как это сумма расходящегося
ин-
теграла![]() и сходящегося по признаку Дирихле
и сходящегося по признаку Дирихле![]() .
.
Обоснуем последнее утверждение:
а)
![]() ;
;
б)
![]() монотонно убывает на
монотонно убывает на![]() ;
;
в)
![]() .
.
Следовательно,
по признаку сравнения в непредельной
форме расходится
![]() ,
а, значит, по признаку сравнения в
предельной форме расходится
,
а, значит, по признаку сравнения в
предельной форме расходится![]() и вместе с ним
и вместе с ним![]() .
.
2.
Исследуем сходимость
![]() .
.
Заметим,
что использовать для исследования
признак Дирихле не представляется
возможным, так как функция
![]() не является монотонной. Поэтому
исследование проведем, используя формулу
Тейлора:
не является монотонной. Поэтому
исследование проведем, используя формулу
Тейлора:
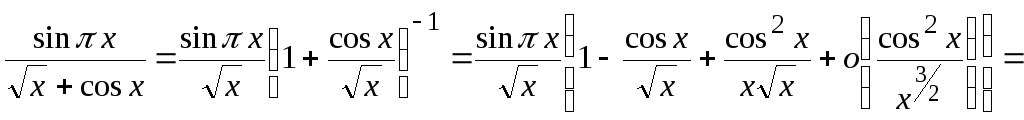
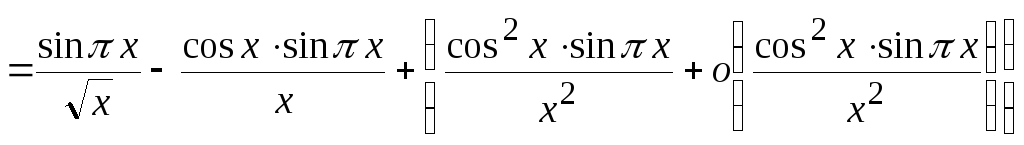
(здесь
мы учли, что
![]() ,
поэтому такое разложение имеет место).
,
поэтому такое разложение имеет место).
Разобьем исходный интеграл на сумму трех интегралов:
![]()
 .
.
Заметим,
что во всех интегралах суммы точка
![]() не является особой, так как подынтегральная
функция ограничена в правосторонней
окрестности точки
не является особой, так как подынтегральная
функция ограничена в правосторонней
окрестности точки![]() .
.
Первый
интеграл этой алгебраической суммы
сходится по признаку Дирихле, так как
![]() монотонно стремится к нулю при
монотонно стремится к нулю при![]() ,
а
,
а![]() .
.
Второй интеграл также сходится по признаку Дирихле, так как
а)
![]()
![]()
![]() ;
;
б)
функция
![]() ,
монотонно убывая, стремится к нулю при
,
монотонно убывая, стремится к нулю при![]() .
.
Третий интеграл сходится абсолютно, так как
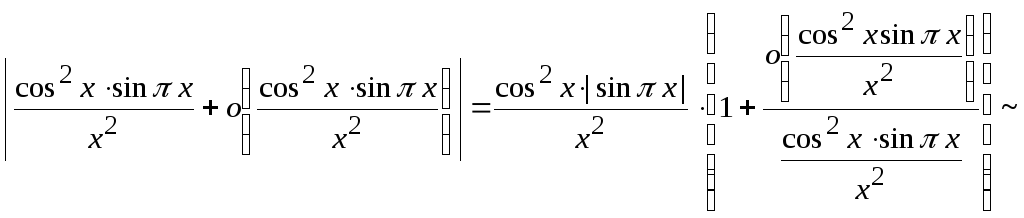
![]() .
.
Следовательно,
из сходимости
![]() по признаку сравнения в непредельной
форме следует сходимость
по признаку сравнения в непредельной
форме следует сходимость![]() .
Тогда по признаку сравнения в предельной
форме сходится и третий интеграл,
составляющий рассматриваемую сумму.
Значит,
.
Тогда по признаку сравнения в предельной
форме сходится и третий интеграл,
составляющий рассматриваемую сумму.
Значит,![]() сходится как сумма интеграла Римана и
исследованного интеграла.
сходится как сумма интеграла Римана и
исследованного интеграла.
Пример
5.
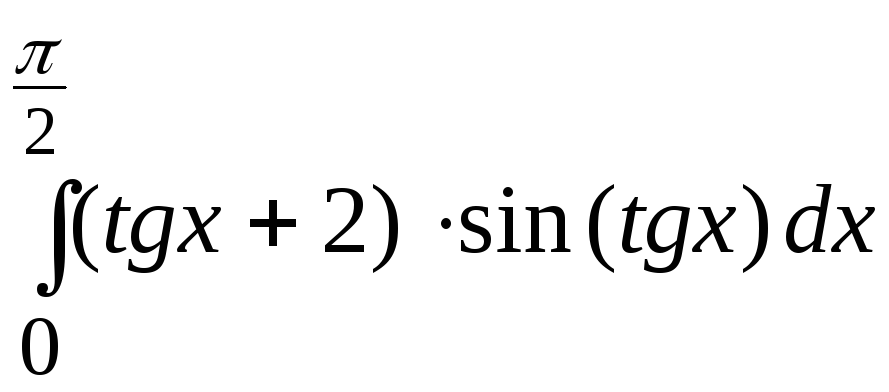 .
.
Функция
![]() ,
в точке
,
в точке![]() функция не определена. Заметим, что
для исследования интеграла удобнее
сделать замену переменной
функция не определена. Заметим, что
для исследования интеграла удобнее
сделать замену переменной![]() ( все условия для проведения такой
замены соблюдены), тогда
( все условия для проведения такой
замены соблюдены), тогда
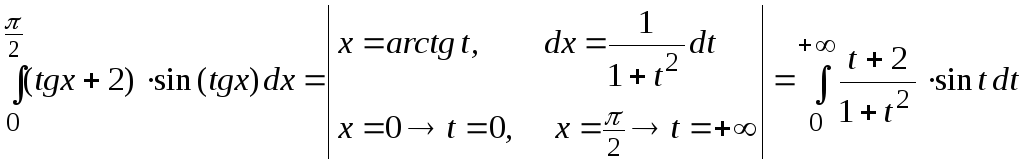 .
.
Нетрудно видеть, что поведение подынтегральной функции более «прозрачно» и привычно для нас в плане исследования.
Заметим,
что
![]() ,
следовательно,
,
следовательно,![]() --
единственная особая точка, функция
--
единственная особая точка, функция![]() не сохраняет знак на
не сохраняет знак на![]() .
.
1.
Исследуем
![]() .
.
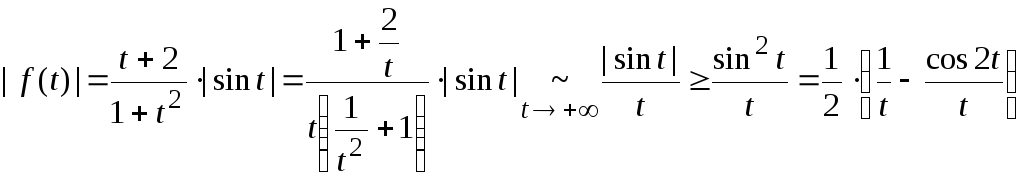 .
.
Так же, как это было сделано в предыдущих примерах нетрудно показать,
что
![]() --
расходится, а
--
расходится, а![]() сходится по признаку Дирихле.
Следовательно, расходится
сходится по признаку Дирихле.
Следовательно, расходится![]() ,
а, значит, расходится и
,
а, значит, расходится и![]() .
.
2.
Исследуем
![]() .
.
а)
![]() ;
;
б)
Покажем, что функция
![]() монотонна.
монотонна.
![]() при
при
![]()
(корни
квадратного трехчлена в числителе
![]() ).
Следовательно,
).
Следовательно,![]() монотонно убывает на
монотонно убывает на![]() .
.
в)
![]() .
.
Отсюда
следует, что
![]() сходится условно (так как нет абсолютной
сходимости).
сходится условно (так как нет абсолютной
сходимости).
Пример
6.
![]() .
.
Функция
![]() ,
следовательно,
,
следовательно,![]() --
единственная особая точка, функция не
сохраняет знак на
--
единственная особая точка, функция не
сохраняет знак на![]() .
.
Исследуем
![]() .
.
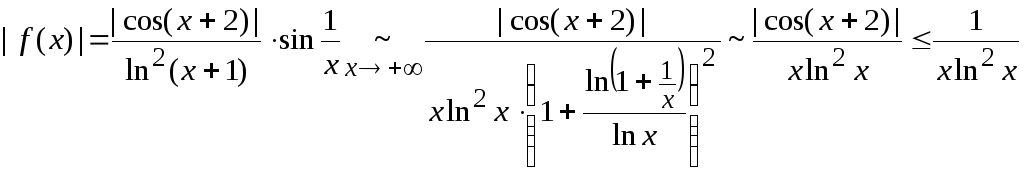 .
.
Рассмотрим
![]() .
.
То
есть
![]() сходится по определению, следовательно,
сходится по определению, следовательно,![]() сходится по признаку сравнения в
непредельной форме. А, значит,
сходится по признаку сравнения в
непредельной форме. А, значит,![]() =
=![]()
![]() -- сходится как сумма интеграла Римана
и рассмотренного несобственного
интеграла. Следовательно, исходный
интеграл сходится абсолютно.
-- сходится как сумма интеграла Римана
и рассмотренного несобственного
интеграла. Следовательно, исходный
интеграл сходится абсолютно.
