
Министерство образования и науки Российской Федерации
Государственное образовательное учреждение
высшего профессионального образования
«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Е.Р.Ляликова, Л.И.Спинко
Несобственные интегралы
Методические указания для студентов 2-го курса
механико-математического факультета РГУ
отделений «Математика» и «Механика»
г. Ростов-на-Дону
2004
Печатается в соответствии с решением кафедры математического анализа Ростовского государственного университета, протокол № 7 от 9 марта 2004 года.
Методическая разработка по теме «Несобственные интегралы» содержит базовый материал для проведения лабораторных занятий на втором курсе механико-математического факультета РГУ по специальностям «Математика» и «Механика». Она также содержит основные теоретические факты, необходимые для решения рассматриваемых задач.
1 Исследование сходимости несобственных
интегралов по определению и их вычисление
Определение
1.Если
![]() --
локально интегрируемая функция на
--
локально интегрируемая функция на![]() и существует конечный предел
и существует конечный предел![]() ,
то говорят, что функция
,
то говорят, что функция![]() интегрируема на
интегрируема на![]() в несобственном смысле, а величину
в несобственном смысле, а величину![]() обозначают символом
обозначают символом![]() и называют сходящимся несобственным
интегралом.
и называют сходящимся несобственным
интегралом.
Сформулируем основные свойства несобственных интегралов.
1.1
Если
![]() то
то![]() и
и![]() .
.
1.2
Если
![]() --
локально интегрируемая функция на
--
локально интегрируемая функция на![]() и
и![]() ,
то
,
то![]() ,
при этом
,
при этом![]() .
.
1.3
Если
![]() ,
то
,
то
![]() .
.
1.4 Критерий Коши сходимости несобственных интегралов
Пусть
![]() ,
,![]() --
единственная особая точка
--
единственная особая точка![]() на
на![]() .
Для того , чтобы
.
Для того , чтобы![]() сходился необходимо и достаточно, чтобы
сходился необходимо и достаточно, чтобы
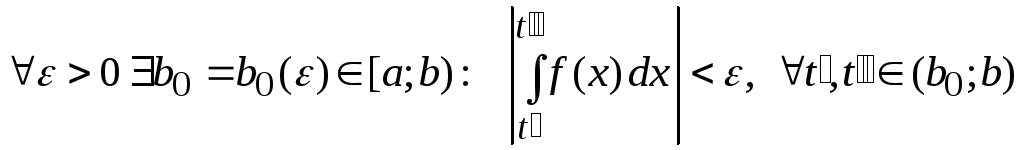 .
.
1.5 Формула Ньютона-Лейбница для несобственных интегралов
Пусть
![]() ,
,![]() --
единственная особая точка
--
единственная особая точка![]() на
на![]() и на
и на![]() функция
функция![]() имеет первообразную
имеет первообразную![]() такую, что существует конечный предел
такую, что существует конечный предел![]() .
Тогда
.
Тогда![]() и
и
![]() .
.
Замена переменных в несобственном интеграле
Пусть
![]() ,
,![]() -непрерывная
функция на
-непрерывная
функция на![]() .
Пусть
.
Пусть![]() ,
причем
,
причем
а)
![]() --
непрерывно дифференцируемая на
--
непрерывно дифференцируемая на![]() функция;
функция;
б)
![]() --
строго монотонная функция на
--
строго монотонная функция на![]() ;
;
в)
![]() .
.
Тогда
интегралы
![]() ,
,![]() сходятся или расходятся одновременно
и, в случае сходимости они равны.
сходятся или расходятся одновременно
и, в случае сходимости они равны.
Интегрирование по частям в несобственном интеграле
Пусть
![]() --
непрерывно дифференцируемые функции
на
--
непрерывно дифференцируемые функции
на![]() и существует конечный предел
и существует конечный предел![]() .
Если один из несобственных интегралов
.
Если один из несобственных интегралов![]() сходится, то сходится и второй, и
справедливо равенство
сходится, то сходится и второй, и
справедливо равенство
![]() ,
где
,
где
![]() .
.
Перейдем к решению задач, в которых требуется исследовать несобственный интеграл на сходимость и, в случае сходимости вычислить его.
Пример
1.
![]() .
.
Функция
![]() (
(![]() --
частное двух непрерывных на
--
частное двух непрерывных на![]() функций). Следовательно
функций). Следовательно![]() --
единственная особая точка. По определению
сходимости несобственного интеграла
имеем:
--
единственная особая точка. По определению
сходимости несобственного интеграла
имеем:
![]()
![]() .
.
Следовательно, исходный интеграл сходится по определению.
Пример
2.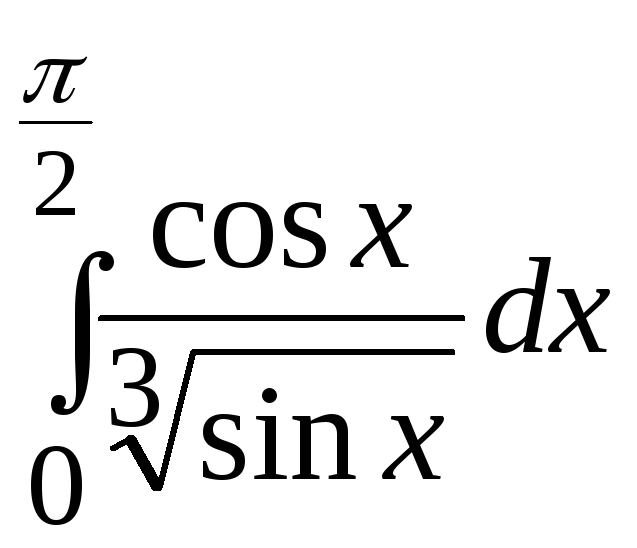 .
.
Функция
![]() ,
в точке
,
в точке![]() не определена, причем
не определена, причем![]() .
Следовательно, функция
.
Следовательно, функция![]() не ограничена в правосторонней окрестности
точки
не ограничена в правосторонней окрестности
точки![]() ,
а потому точка
,
а потому точка![]() --
единственная особая точка. По определению
сходимости несобственного интеграла
--
единственная особая точка. По определению
сходимости несобственного интеграла
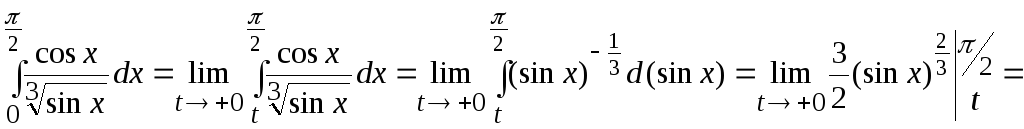
![]() .
.
Следовательно, исходный интеграл сходится по определению.
Пример
3.
![]() .
.
Функция
![]() ,
следовательно,
,
следовательно,![]() единственная особая точка. По определению
сходимости несобственного интеграла
единственная особая точка. По определению
сходимости несобственного интеграла
![]()
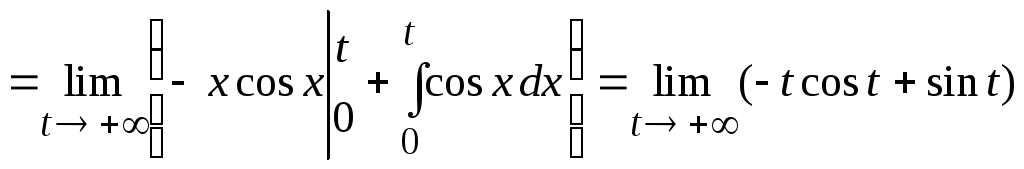 .
.
Здесь мы использовали теорему I.7 об интегрировании по частям несобственного интеграла. Так как последний предел не существует, то по определению несобственный интеграл расходится.
Пример
4.![]() .
.
Функция
![]() ,
следовательно,
,
следовательно,![]() единственная особая точка. По определению
сходимости несобственного интеграла
единственная особая точка. По определению
сходимости несобственного интеграла
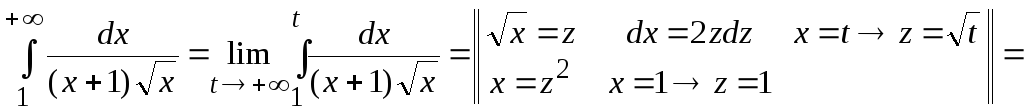
![]() .
.
Здесь мы применили теорему I.6 о замене переменной (заметим, что все условия этой теоремы выполнены).
Упражнения
Исследовать на сходимость и в случае сходимости вычислить следующие несобственные интегралы:
1.
![]() 2.
2.
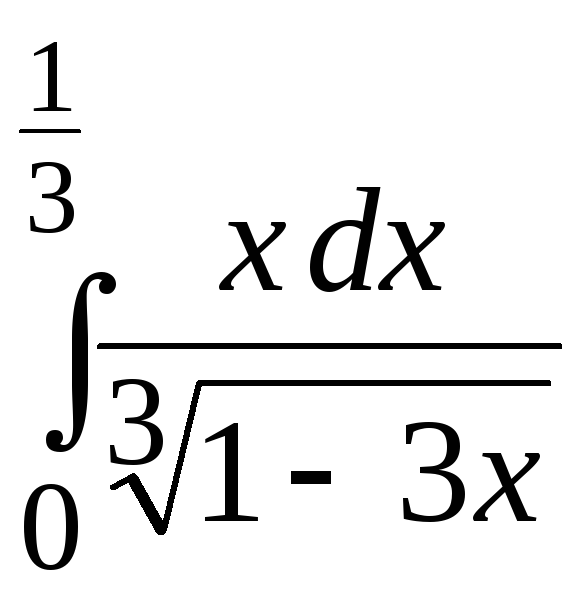 3.
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.![]() 7.
7.
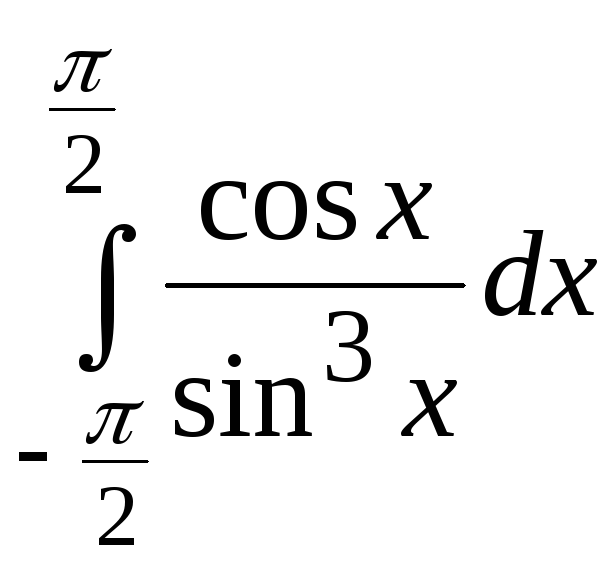 8.
8.
![]()
9.
![]() 10.
10.![]() 11.
11.![]() 12.
12.
![]() .
.
2 Несобственные интегралы от неотрицательных функций
2.1 Первый признак сравнения (непредельная форма признака сравнения)
Пусть
![]() ,
,![]() ,
и пусть
,
и пусть![]() --единственная
особая точка
--единственная
особая точка![]() и
и![]() на
на![]() .
Тогда
.
Тогда
а)
если
![]() сходится, то
сходится, то![]() сходится;
сходится;
б)
если
![]() расходится, то
расходится, то![]() расходится.
расходится.
Второй признак сравнения (предельная форма признака
сравнения)
Пусть
![]() ,
,![]() ,
,![]() --единственная
особая точка
--единственная
особая точка![]() и
и![]() на
на![]() .
Если
.
Если![]() и
и![]() сохраняет знак в окрестности точки
сохраняет знак в окрестности точки![]() и существует предел
и существует предел![]() ,
то несобственные интегралы
,
то несобственные интегралы![]() и
и![]() сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
