
Теория игр / Лекция 3
.pdf
1
МАТРИЧНЫЕ ИГРЫ
Е.В. Яроцкая, к.э.н., доцент кафедры экономики ТПУ

2
Тема 2: Матричные игры
2.1. Равновесная ситуация
2.2. Смешанные стратегии
2.3. Упрощение матричной игры 2.4. Графический метод решения
матричных игр в смешанных стратегиях 2.5. Решение игр 2xn и mx2
Е.В. Яроцкая, к.э.н., доцент кафедры экономики ТПУ
2.1. Равновесная ситуация |
3 |
|
Пусть в игре участвуют два игрока А и В
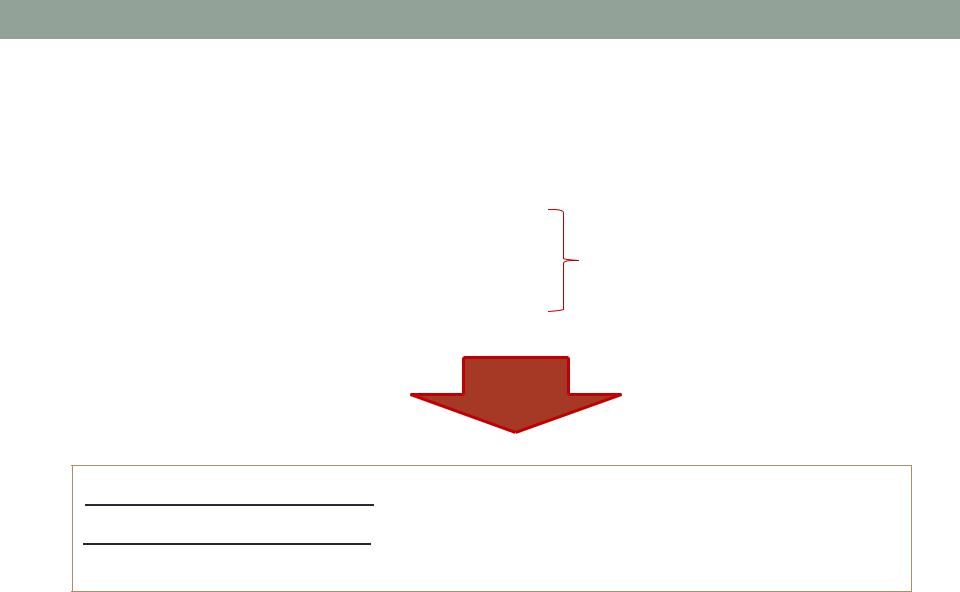
выигрыш игрока А → аij, |
|
|
аij = – bj |
||
выигрыш игрока В → bj |
||
|
Задача игрока А - максимизировать свой выигрыш. Задача игрока В – минимизировать свой проигрыш или минимизировать выигрыш первого игрока.
Е.В. Яроцкая, к.э.н., доцент кафедры экономики ТПУ
2.1. Равновесная ситуация |
4 |
|
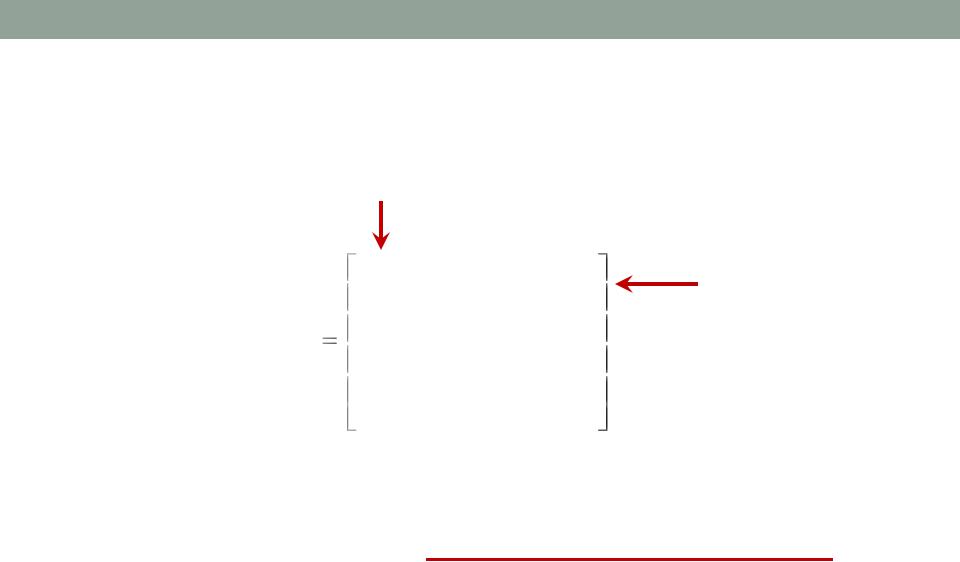
Игру можно представить в виде матрицы строки которой - стратегии игрока А, а столбцы – стратегии игрока В.
стратегии игрока В
a11 |
a12 |
... |
a1n |
стратегии |
a21 |
a22 |
... |
a2 n |
игрока А |
|
||||
A |
|
|
|
|
... ... ... ... |
|
|||
am1 |
am 2 |
... |
am n |
|
Матрица называется платежной матрицей, где элементы этой матрицы это выигрыши игрока А.
Е.В. Яроцкая, к.э.н., доцент кафедры экономики ТПУ

2.1. Равновесная ситуация |
5 |
|
Оптимальной стратегией игрока в матричной игре называется такая, которая обеспечивает ему максимальный выигрыш.
Задача каждого из игроков – найти наилучшую стратегию игры
Е.В. Яроцкая, к.э.н., доцент кафедры экономики ТПУ

2.1. Равновесная ситуация |
6 |
|
ПРИНЦИП МАКСМИНА:
необходимо выбрать ту стратегию, чтобы при наихудшем поведении противника получить максимальный выигрыш.
Е.В. Яроцкая, к.э.н., доцент кафедры экономики ТПУ
2.1. Равновесная ситуация |
7 |
|
Пример.
Платежная матрица имеет следующий вид
7 9 10
A 3 4 8
7 5 8
Е.В. Яроцкая, к.э.н., доцент кафедры экономики ТПУ

2.1. Равновесная ситуация |
8 |
|
Решение:
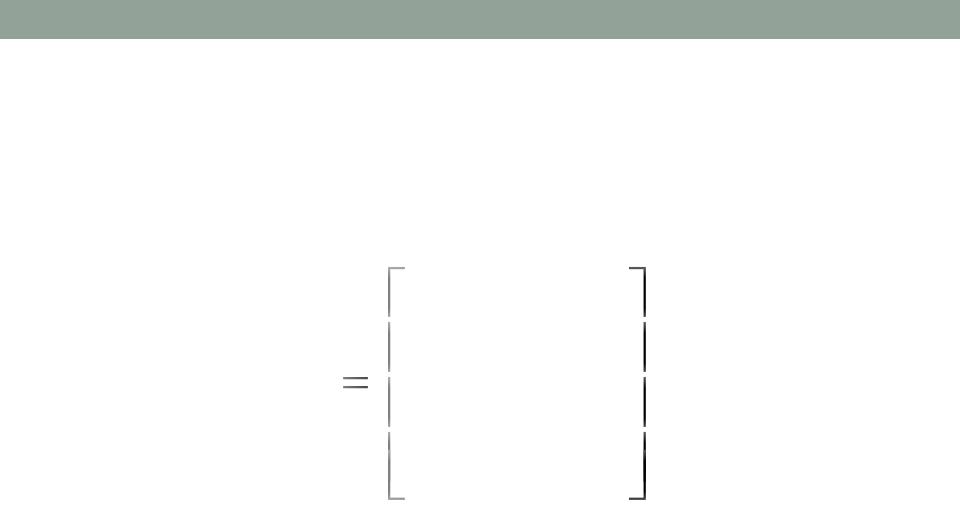
Найдем наилучшую стратегию игрока А (строки) – это минимальное число в каждой строке матрицы
|
|
|
|
|
|
|
i |
min aij , i |
1, m |
||||
|
|
|
|
|
|
|
|
|
|
|
αi |
||
|
7 |
9 |
10 |
7 |
|
|
A |
3 |
4 |
8 |
3 |
|
|
|
7 |
5 |
8 |
5 |
|
|
Е.В. Яроцкая, к.э.н., доцент кафедры экономики ТПУ
2.1. Равновесная ситуация |
9 |
|
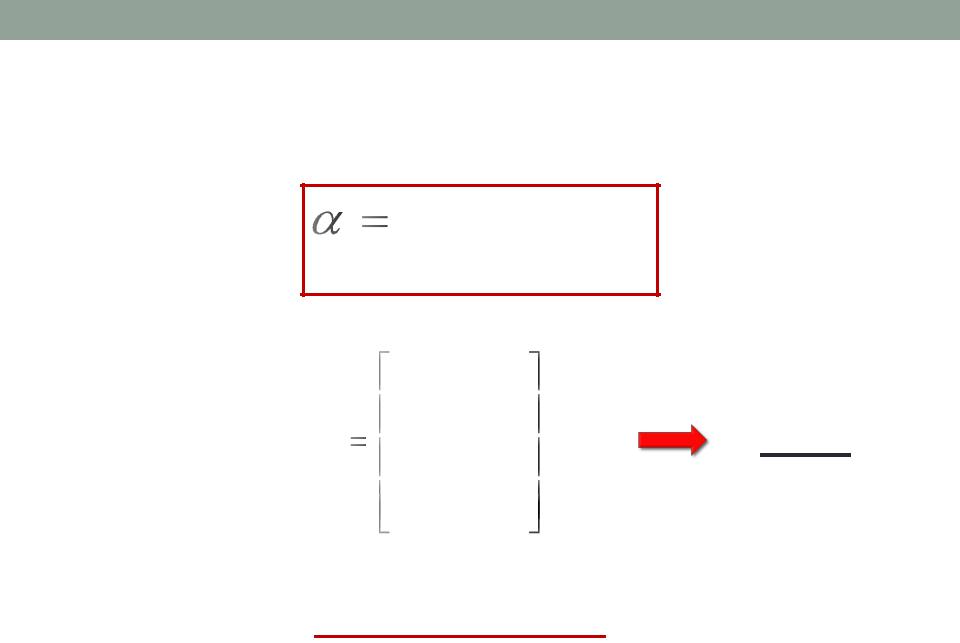
Зная минимальные выигрыши при различных стратегиях Аi , игрок А выберет ту стратегию, для которой αi максимально.
max min aij
i j
αi
7 9 10 7
A 3 4 8 3 |
α = 7 |
7 5 8 5
Величина α – гарантированный выигрыш игрока А и называется нижней ценой игры (максимином)
Е.В. Яроцкая, к.э.н., доцент кафедры экономики ТПУ
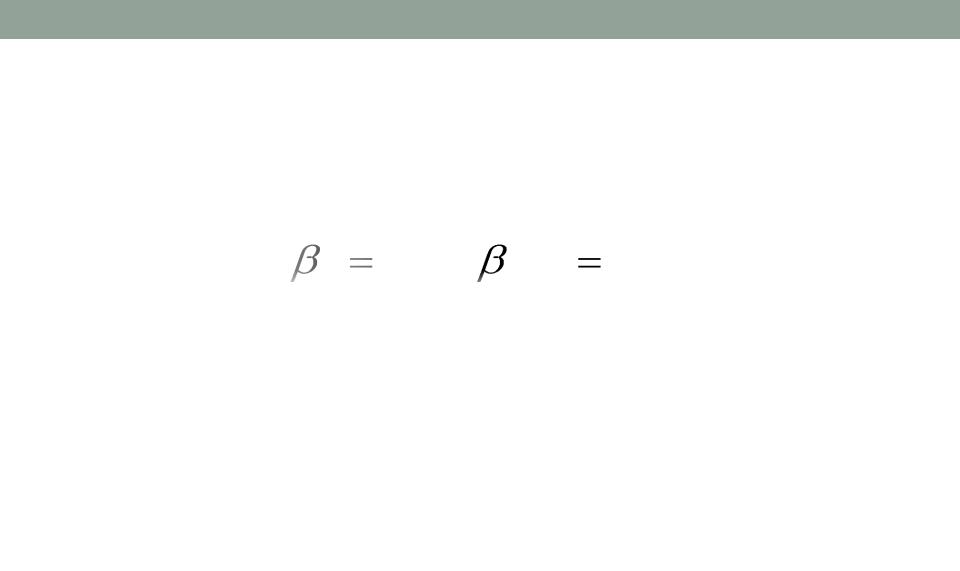
2.1. Равновесная ситуация |
10 |
|
Далее необходимо определить наилучшую стратегию игрока В (столбцы) – это максимальное число в каждом столбце матрицы
|
|
|
|
|
|
|
j |
max |
|
j , j 1, n |
|||
|
|
|
|
|
|
|
|
|
9 |
10 |
|
|
|
|
7 |
|
|
|
||
А= |
3 |
4 |
8 |
|
|
|
|
7 |
5 |
8 |
|
|
|
βj |
7 |
9 |
10 |
|
|
|
Е.В. Яроцкая, к.э.н., доцент кафедры экономики ТПУ
