|
ЗАДАНИЕ
N 1
(-
введите ответ)
(I.
стр.13)
Дана
матрица
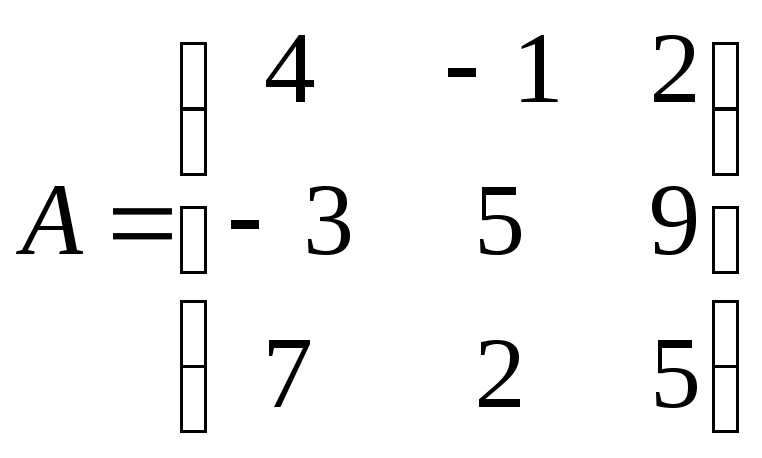 .
Тогда алгебраическое дополнение
элемента .
Тогда алгебраическое дополнение
элемента
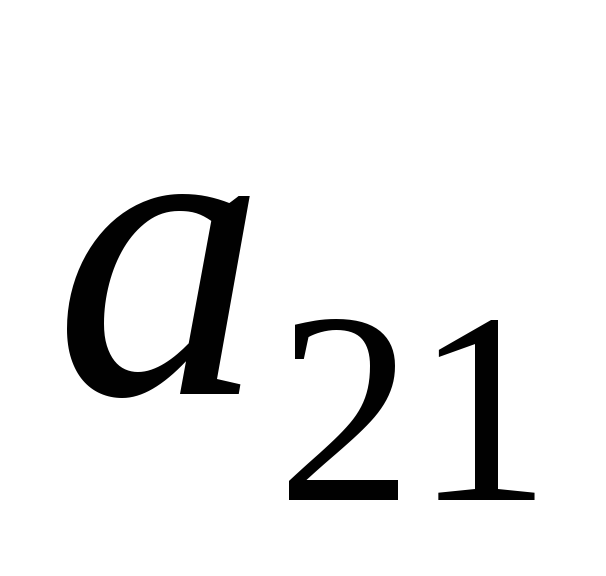 равно …
равно …
Решение:
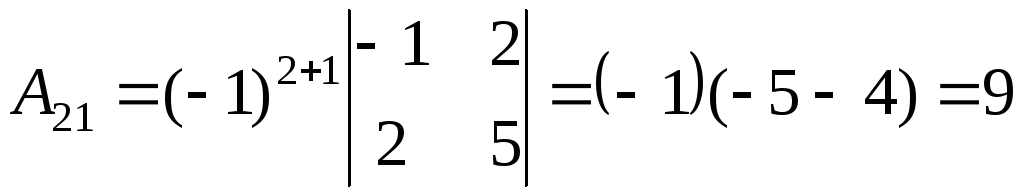 . .
ЗАДАНИЕ
N 2
(-
выберите несколько вариантов
ответа)
(I.
стр.10)
Если
существует матрица
 ,
то матрица ,
то матрица

ВАРИАНТЫ
ОТВЕТОВ:
1)
является
квадратной 2)
может
быть единичной
3)
может
быть произвольной 4)
является
нулевой (размера
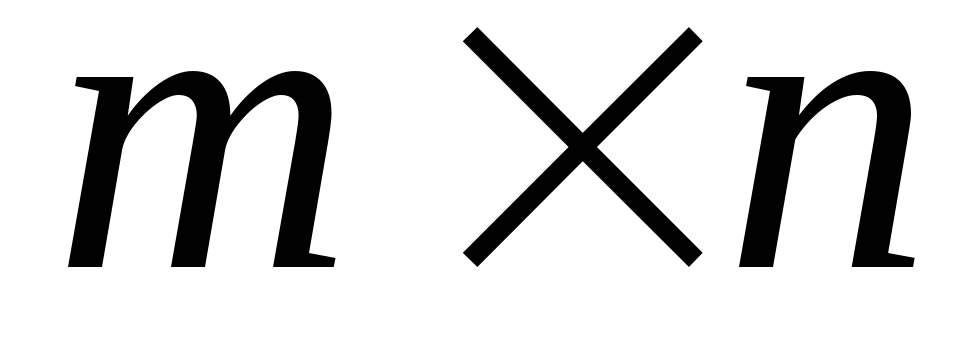 ,
где ,
где
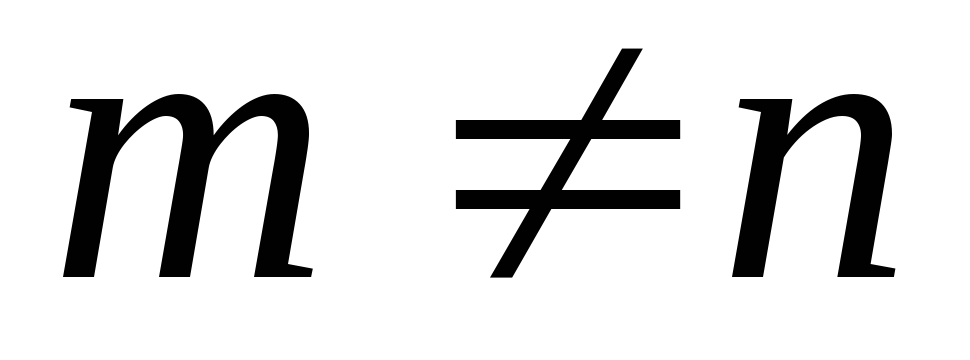 ) )
Решение:
Пусть матрица
 размера
размера
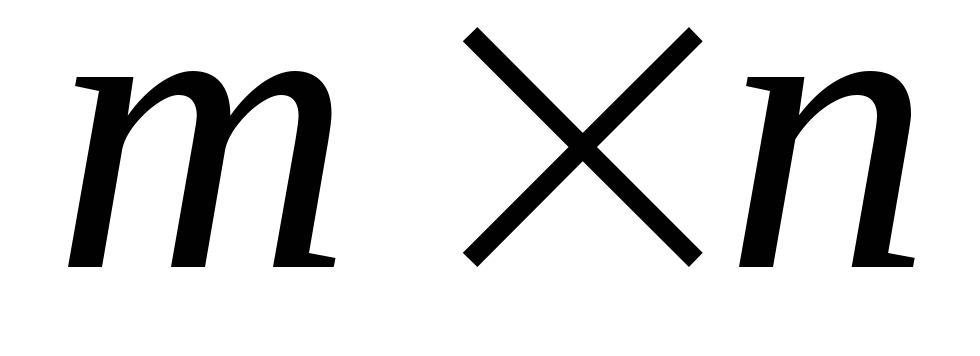 ,
тогда матрица ,
тогда матрица
 имеет размер
имеет размер
 .
Разность матриц .
Разность матриц
 и
и
 будет определена если
будет определена если
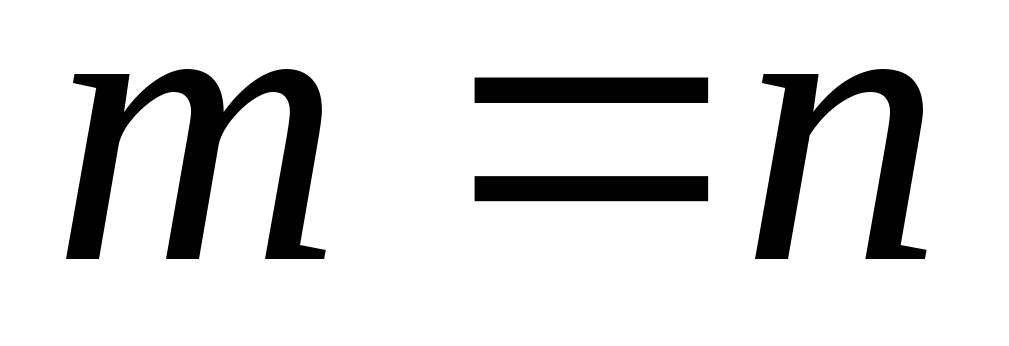 . .
Ответ:
1), 2).
ЗАДАНИЕ
N 3
(-
выберите варианты согласно тексту
задания)
(I.
стр.10)
Даны
матрицы
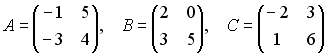 .
Установите
соответствие между двумя
множествами .
Установите
соответствие между двумя
множествами
1.
 ,
2. ,
2.
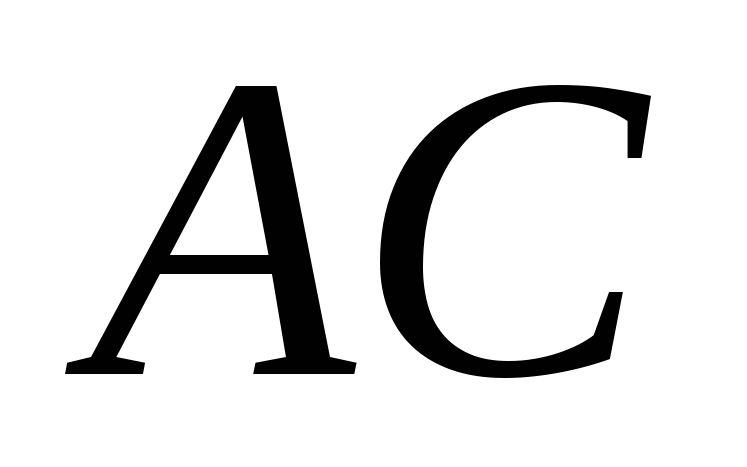 ,
3. ,
3.
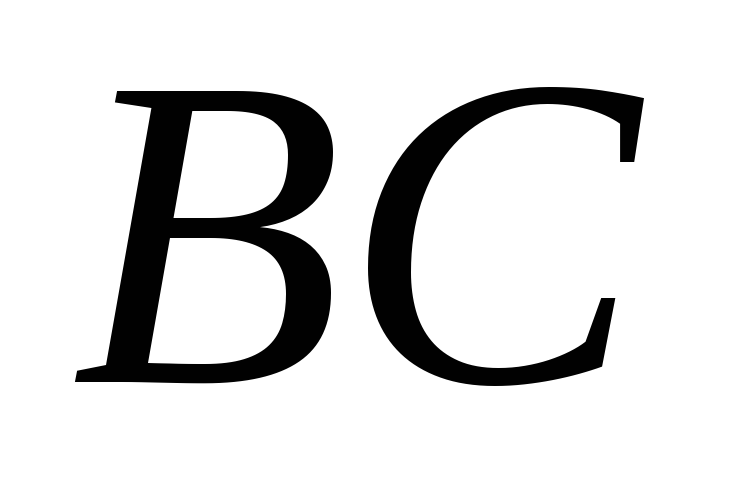 . .
Варианты
ответов:
А)
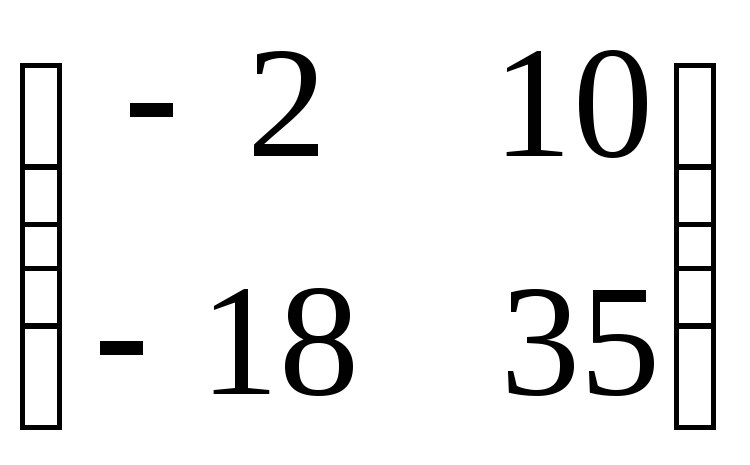 ,
B) ,
B)
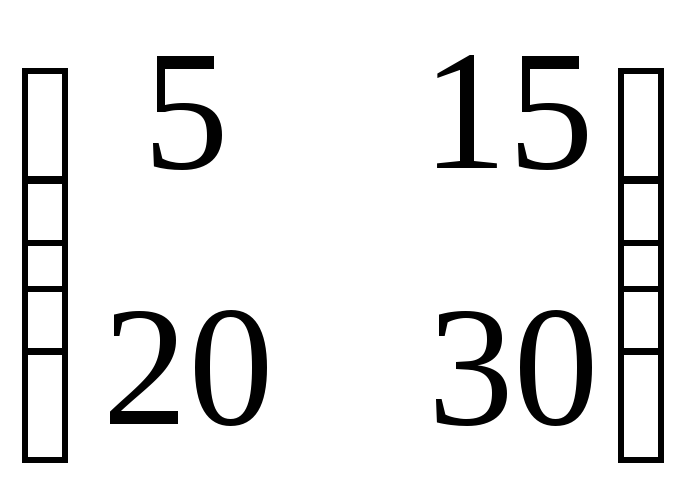 ,
C) ,
C)
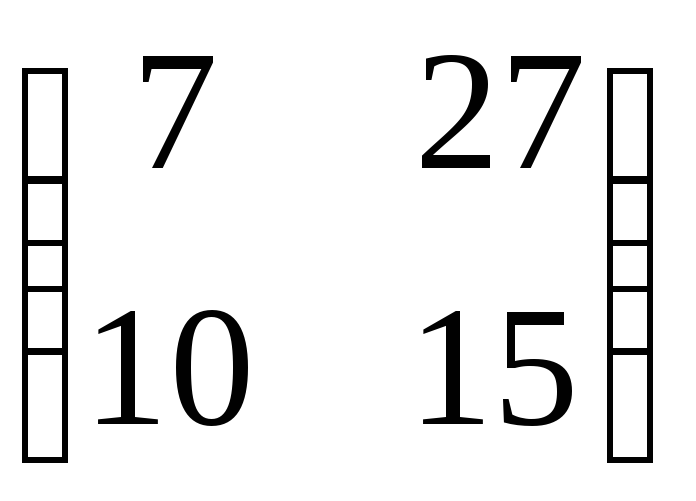 ,
D) ,
D)
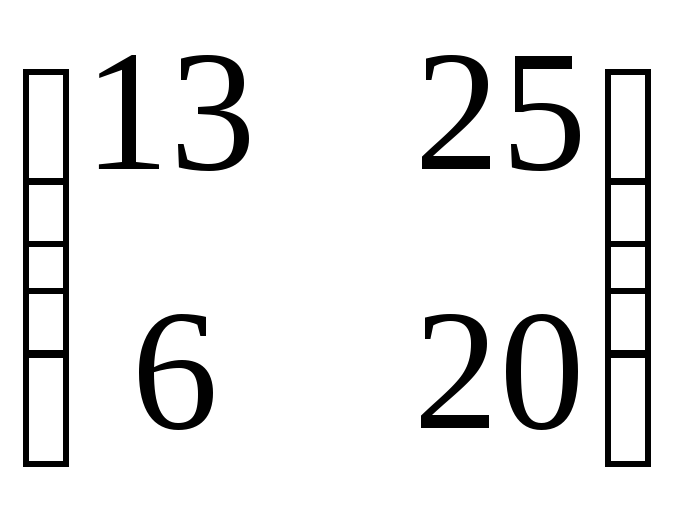 , E)
, E)
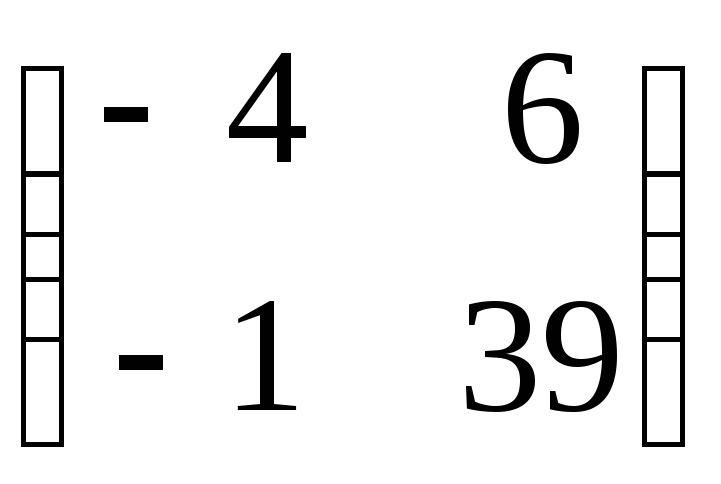 . .
Решение:
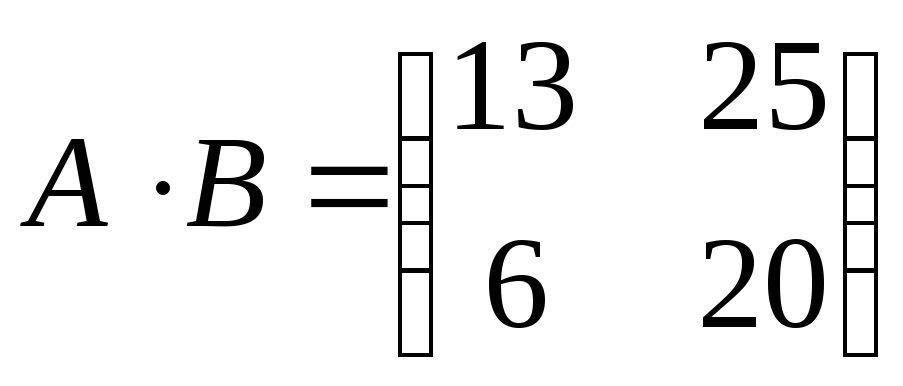 , ,
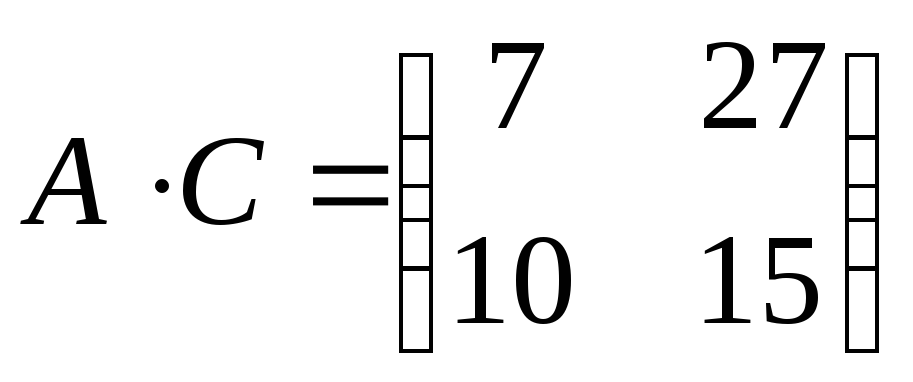 , ,
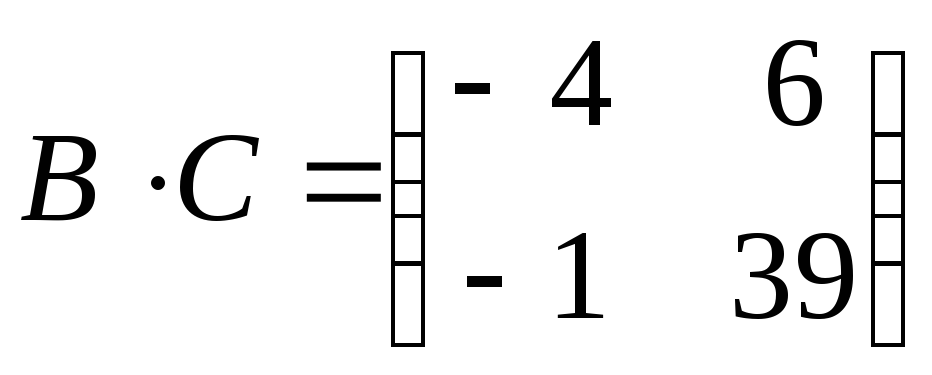 . .
Ответ:
1. D,
2. D,
2. C,
3. C,
3. E. E.
ЗАДАНИЕ
N 4
(-
выберите один вариант ответа)
(I.
стр.30), (II.
стр.57)
В
системе уравнений  базисными
(несвободными) переменными можно
считать… базисными
(несвободными) переменными можно
считать…
Варианты
ответов:
1)
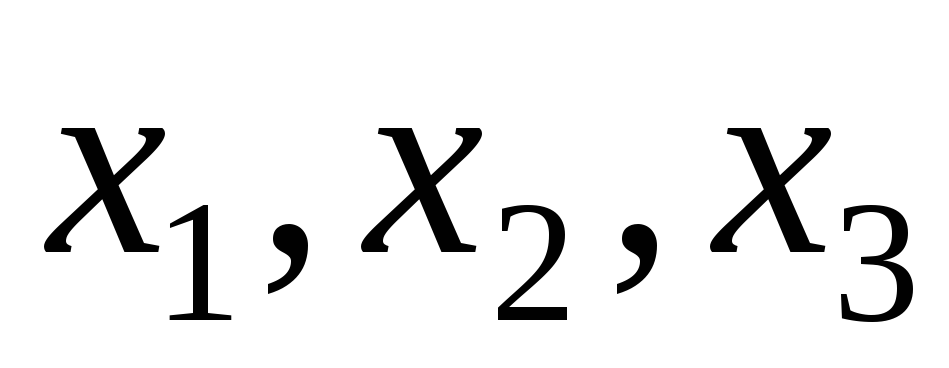 ,
2) ,
2)
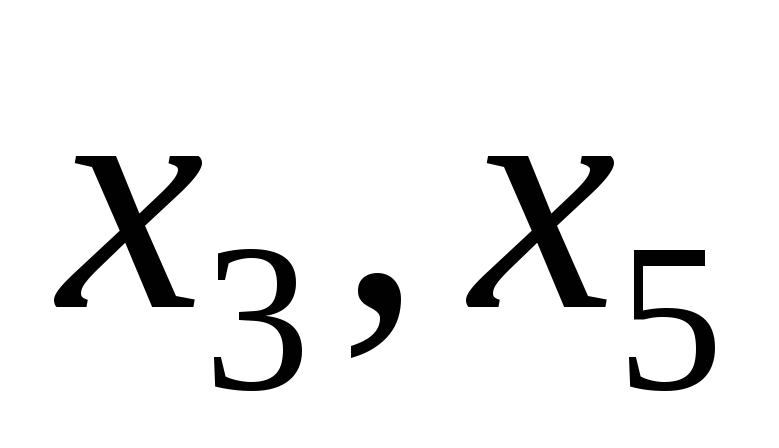 ,
3) ,
3)
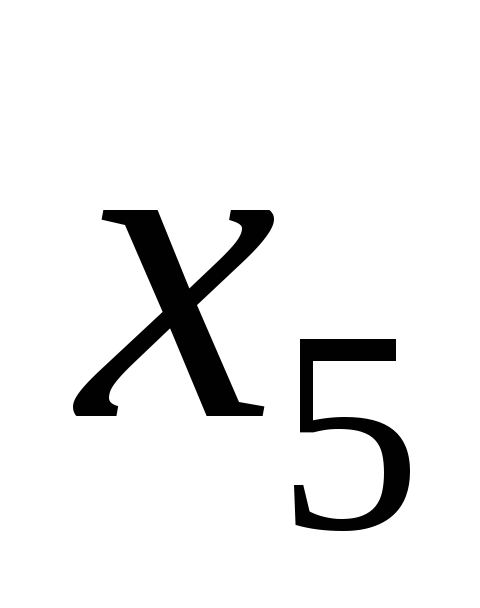 ,
4) ,
4)
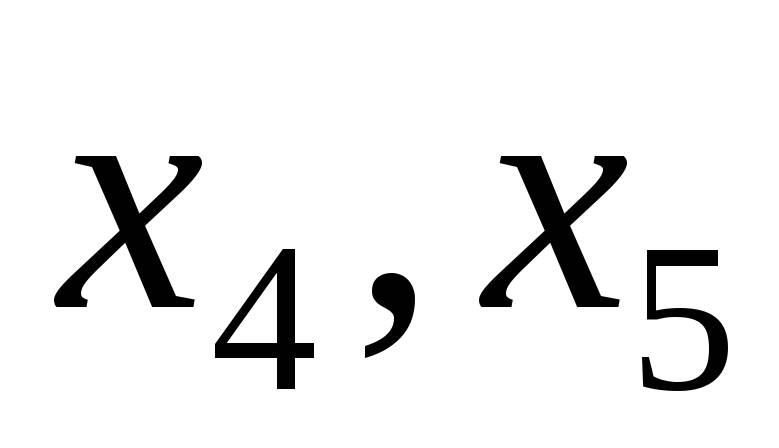 . .
Решение:
Так как имеется система третьего
порядка, то базисными могут быть
три переменными.
Ответ:
1)
ЗАДАНИЕ
N 5
(-
выберите один вариант ответа)
Матрице
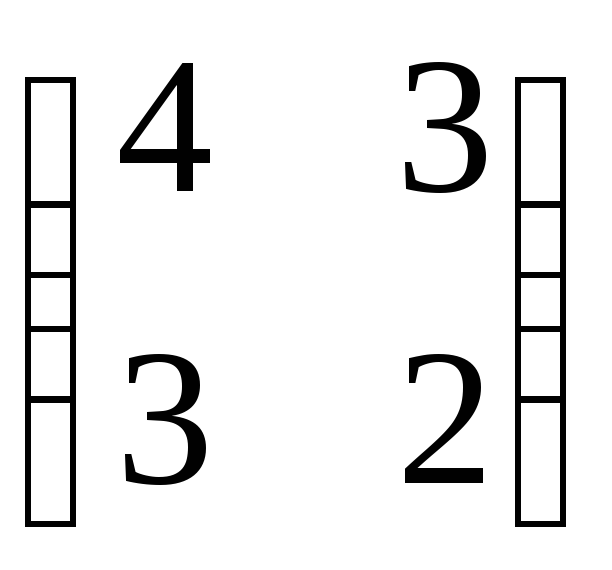 соответствует
квадратичная форма … соответствует
квадратичная форма …
Варианты
ответов:
1)
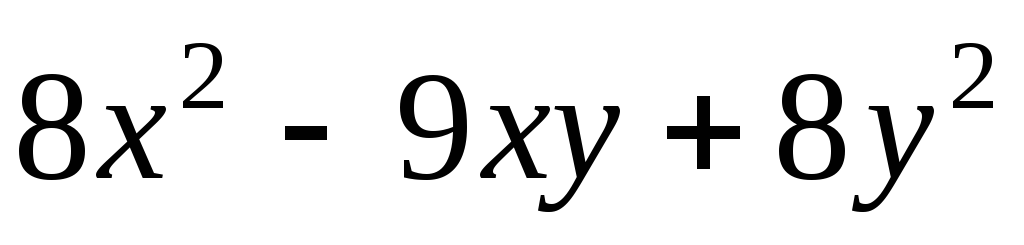 ,
2) ,
2)
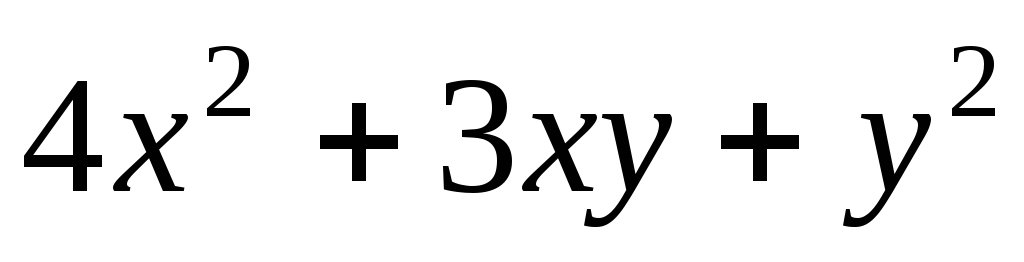 ,
3) ,
3)
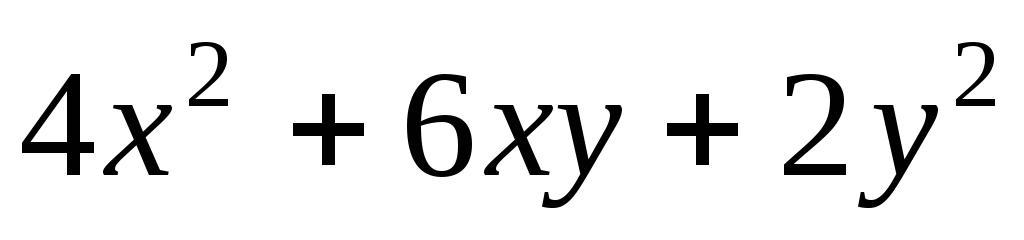 ,
4) ,
4)
 . .
Решение:
Найдем квадратичную форму
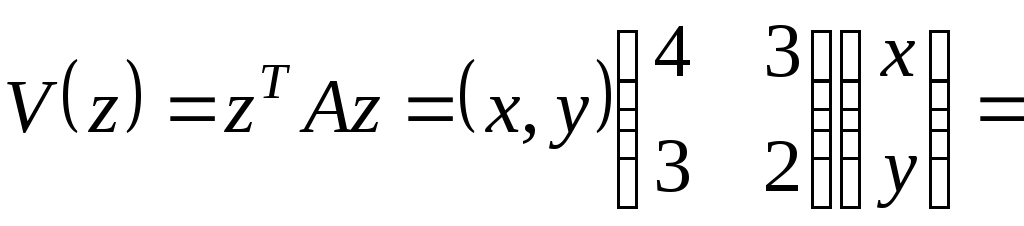
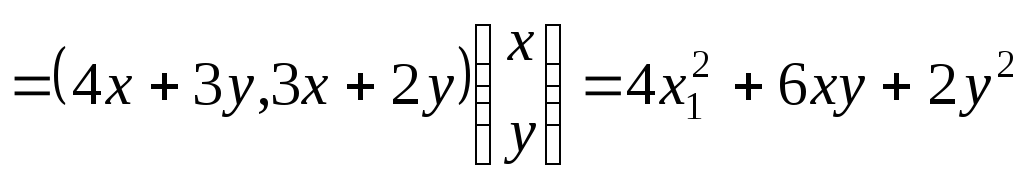 . .
Ответ:
3)
ЗАДАНИЕ
N 6
(-
введите ответ)
(I.
стр.13)
Если
определитель
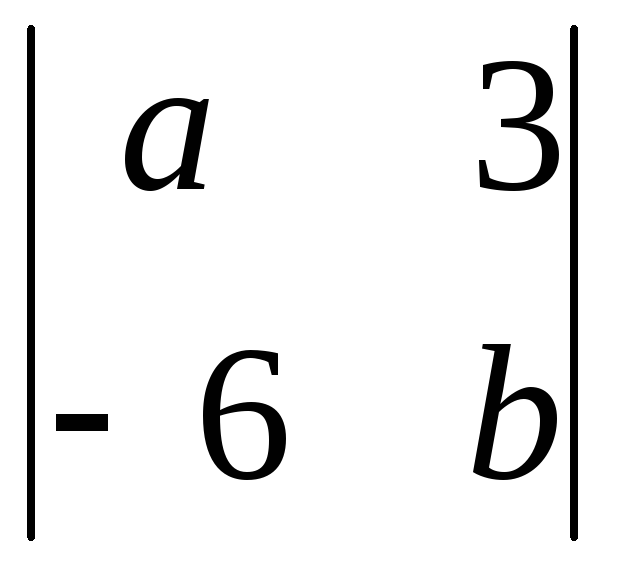 равен равен
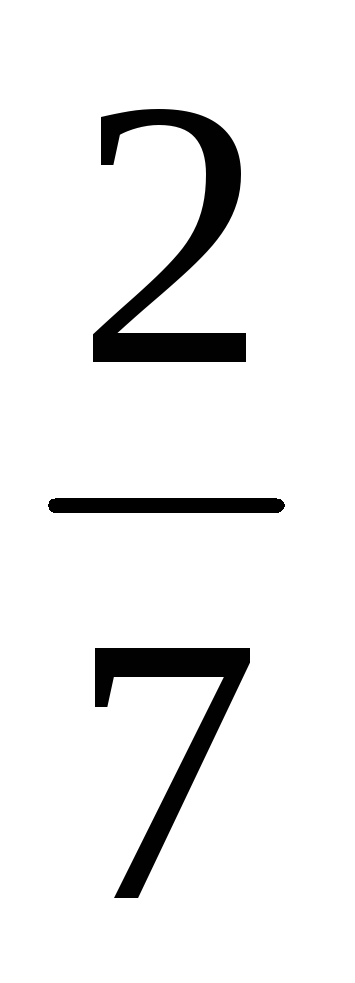 ,
то определитель ,
то определитель
 равен …
равен …
Решение:
По условию задачи
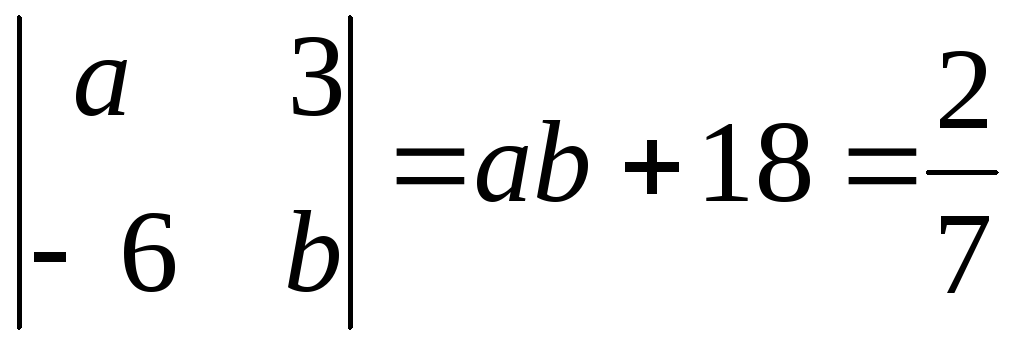 .
Найдем определитель по первой
строке .
Найдем определитель по первой
строке
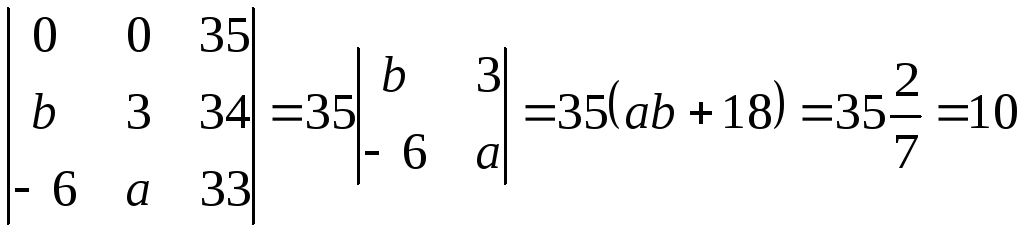 . .
Ответ:
10
ЗАДАНИЕ
N 7
(-
выберите варианты согласно тексту
задания)
(I.
стр.49)
Установите
соответствие между функцией и
её областью определения
1.
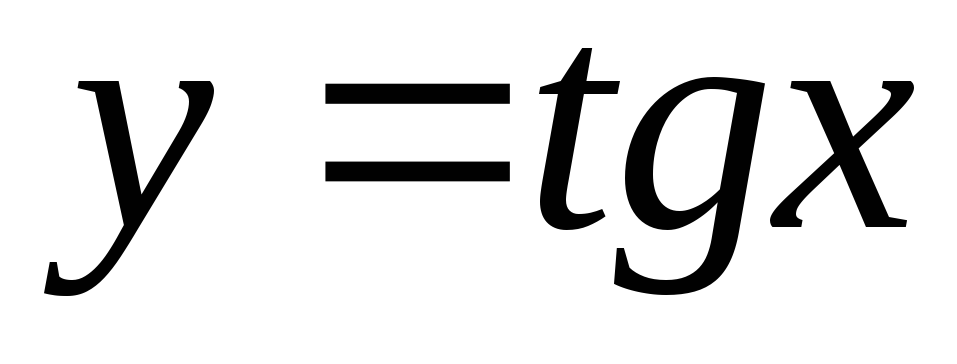 ,
2. ,
2.
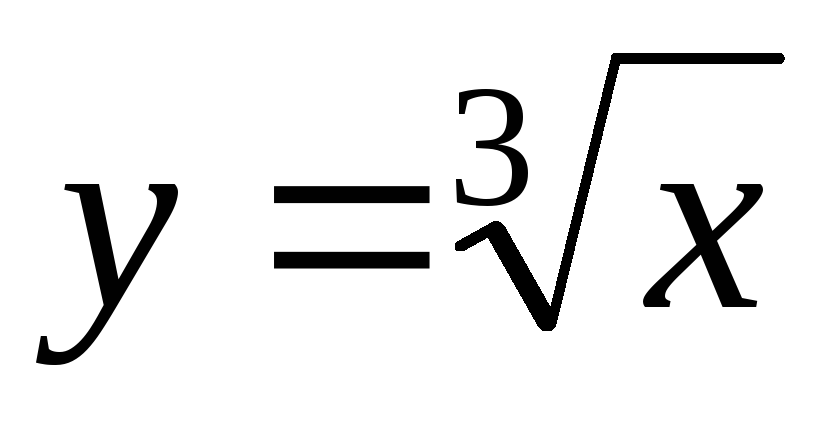 ,
3. ,
3.
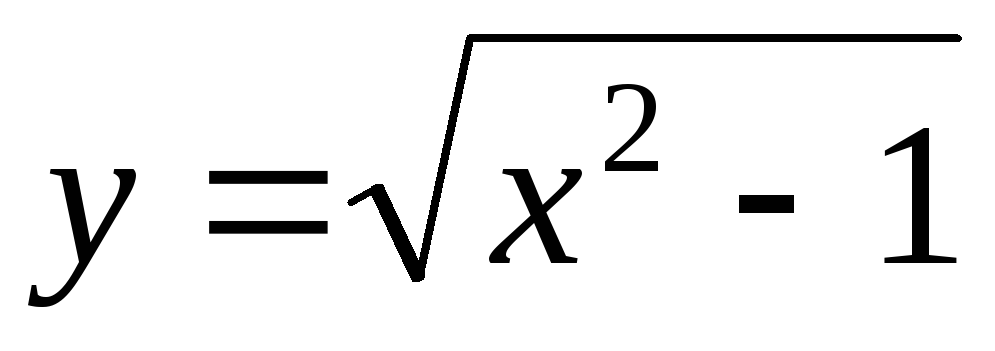
Варианты
ответов:
A)
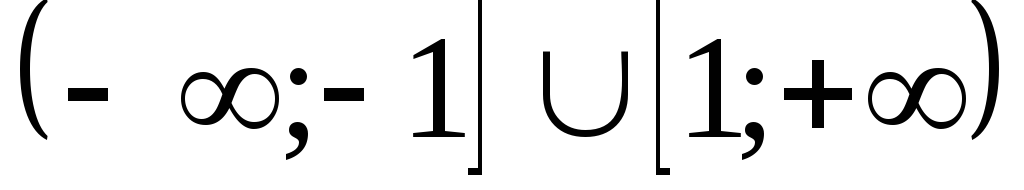 ,
B) ,
B)
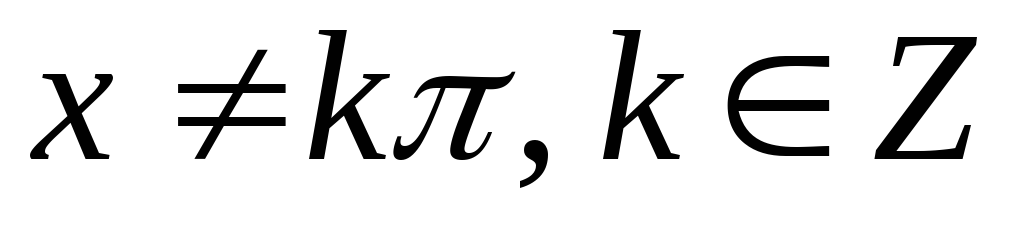 ,
C) ,
C)
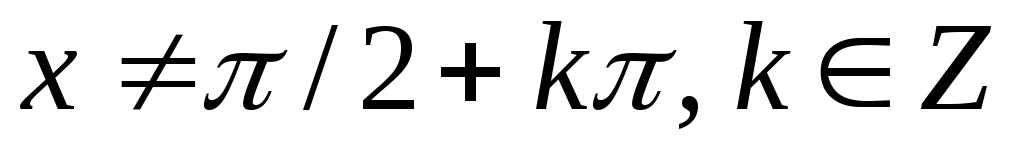 ,
D) ,
D)
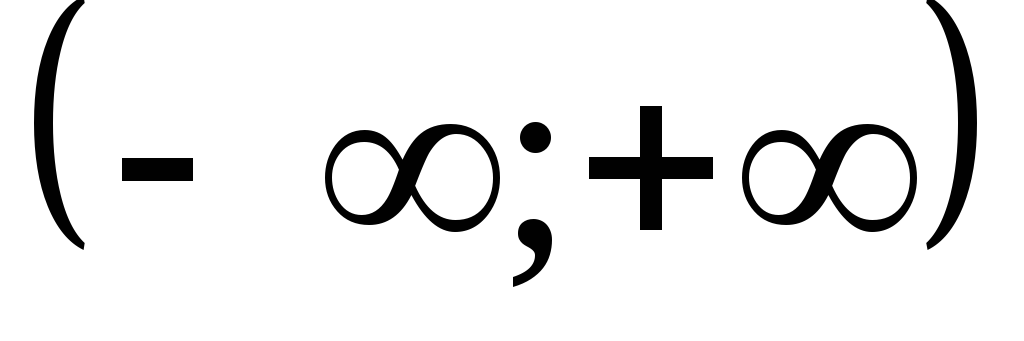 ,
E) ,
E)
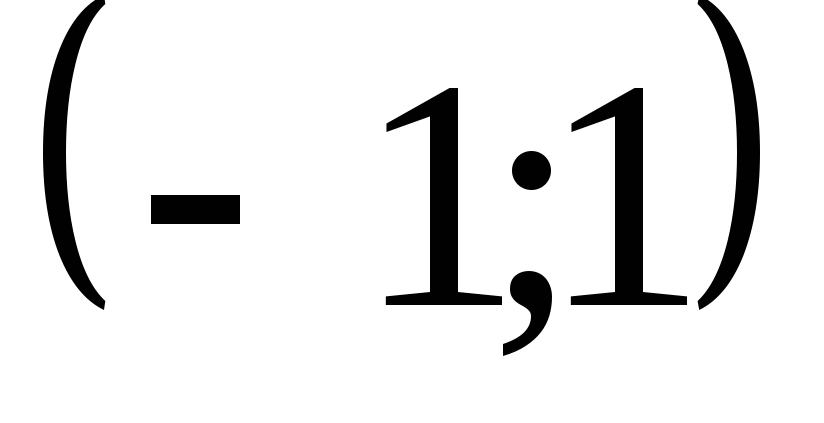 . .
Ответ:
1. C,
2. C,
2. D,
3. D,
3. A. A.
ЗАДАНИЕ
N 8
(-
выберите несколько вариантов
ответа)
(I.
стр.49)
Конечный
предел при
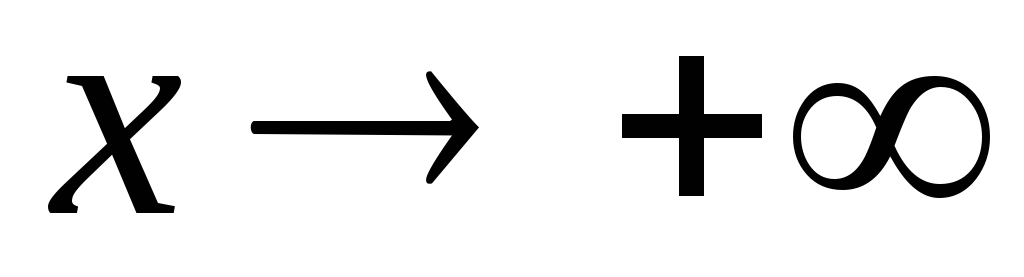 имеют
следующие функции … имеют
следующие функции …
Варианты
ответов:
1)
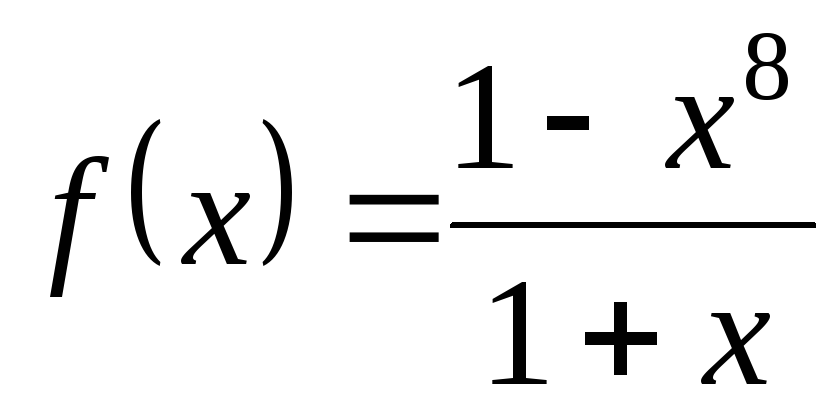 ,
2) ,
2)
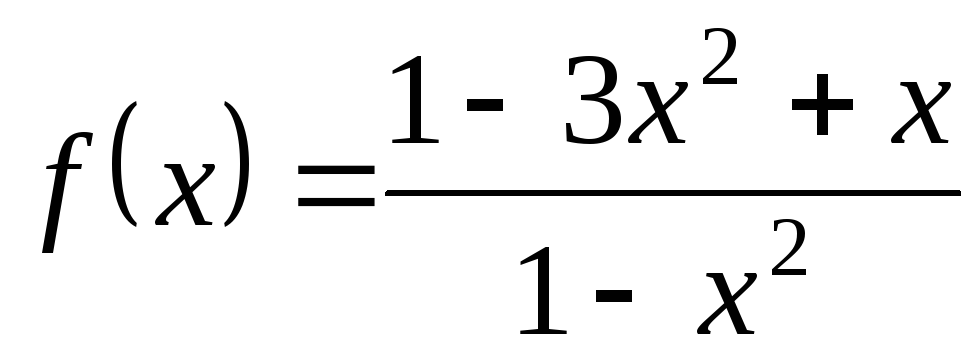 ,
3) ,
3)
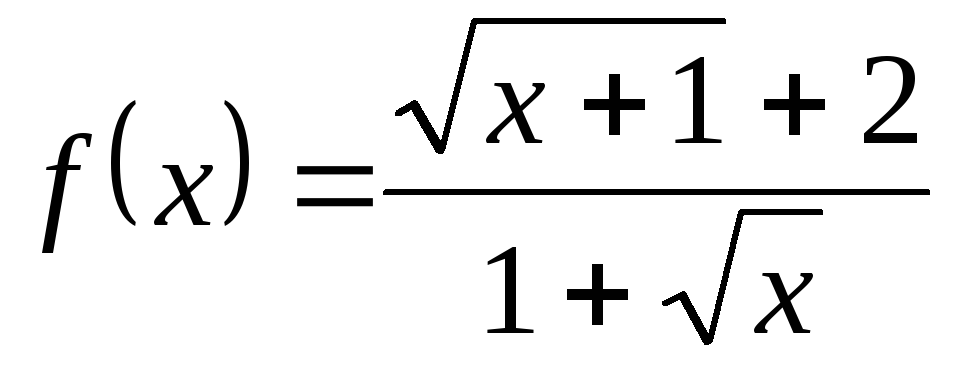 ,
4) ,
4)
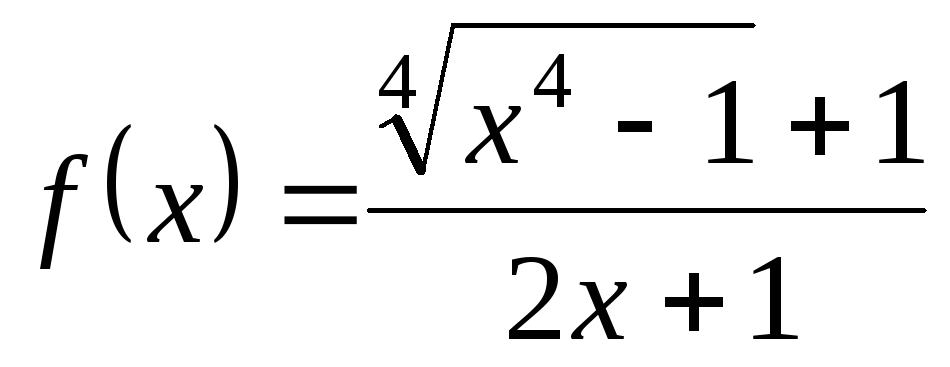 . .
Решение:
Функция имеет конечный предел,
если степень числителя меньше
или равна степени знаменателя.
Ответ:
2), 3).
ЗАДАНИЕ
N 9
(-
введите ответ)
(I.
стр.62)
Функция
задана графически. Определите
количество точек, принадлежащих
интервалу
 ,
в которых не существует производная
этой функции. ,
в которых не существует производная
этой функции.
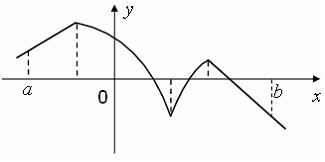
Ответ:
3
ЗАДАНИЕ
N 10
(-
выберите варианты согласно тексту
задания)
(I.
стр.61)
Установите
соответствие между функцией и
ее производной:
1.
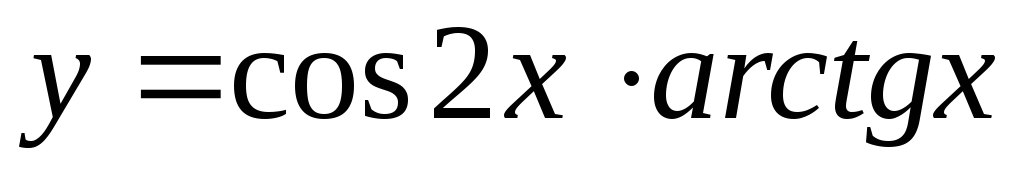 , 2.
, 2.
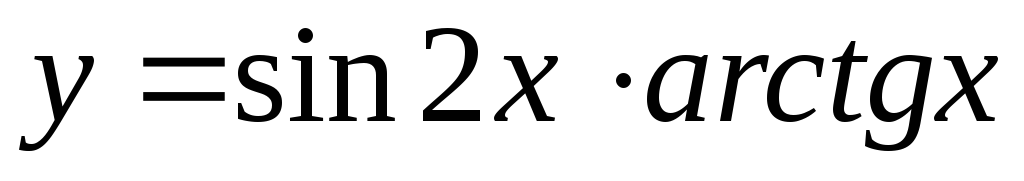 , 3.
, 3.
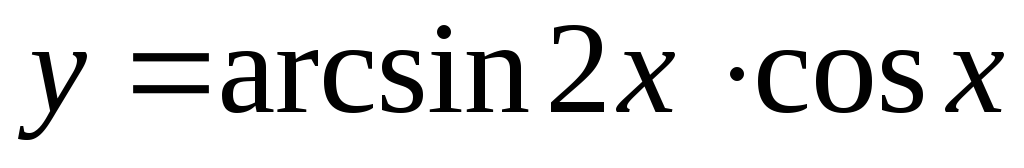 . .
Варианты
ответов:
A)
 ,
B) ,
B)
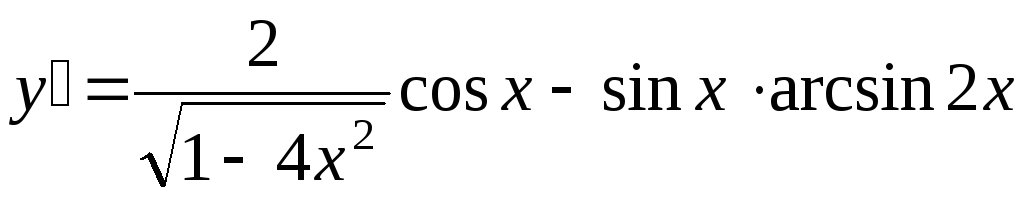 ,
C) ,
C)
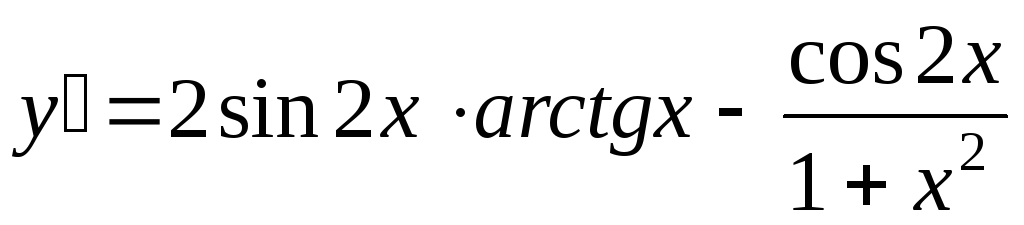 ,
D) ,
D)
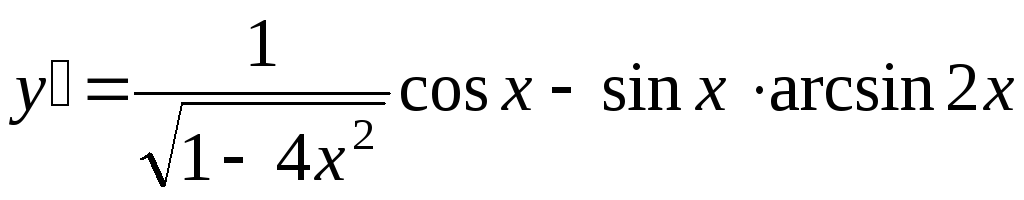 ,
E) ,
E)
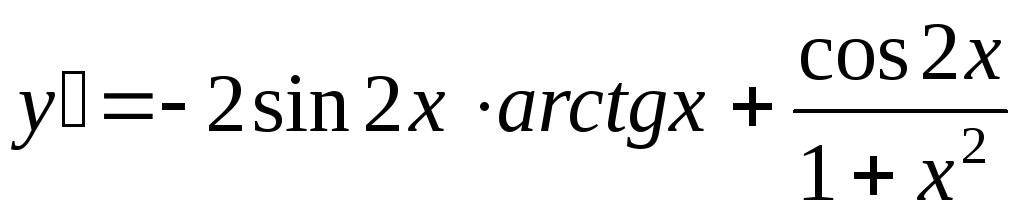 . .
Ответ:
1. E,
2. E,
2. A,
3. A,
3. B. B.
ЗАДАНИЕ
N 11
(-
выберите один вариант ответа)
(I.
стр.62)
Значение
производной второго порядка
функции
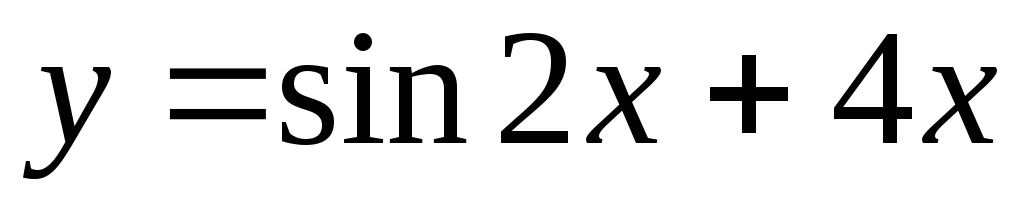 в
точке в
точке
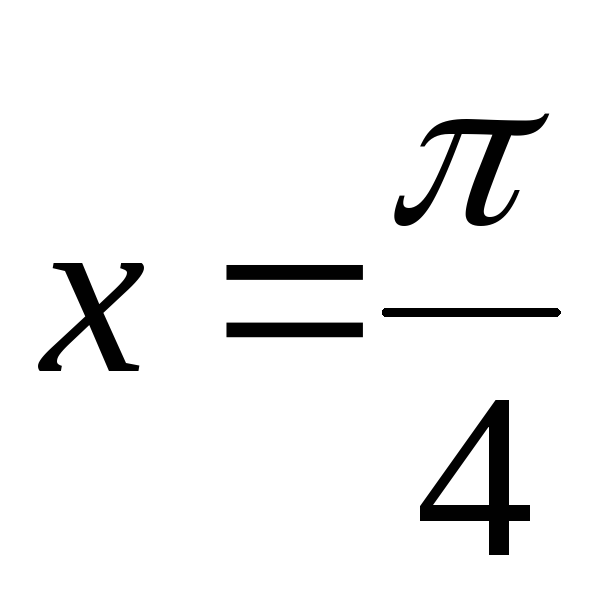 равно…
равно…
Варианты
ответов:
1)
4,
2)
-1,
3)
-4,
4) 1.
Решение:
Найдем
 , ,
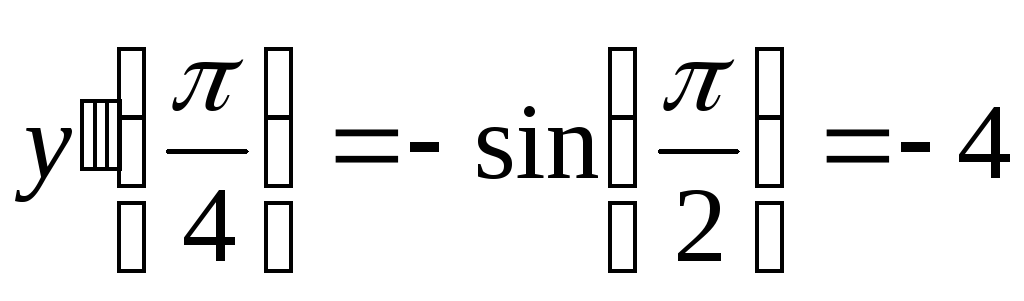 . .
Ответ:
3)
ЗАДАНИЕ
N 12
(-
выберите варианты согласно тексту
задания)
(I.
стр.67)
Функция
 задана
графиком на отрезке задана
графиком на отрезке
 . .
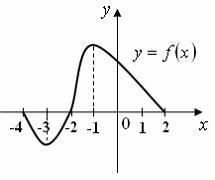
Установите
соответствие между заданными
условиями и промежутками.
1)
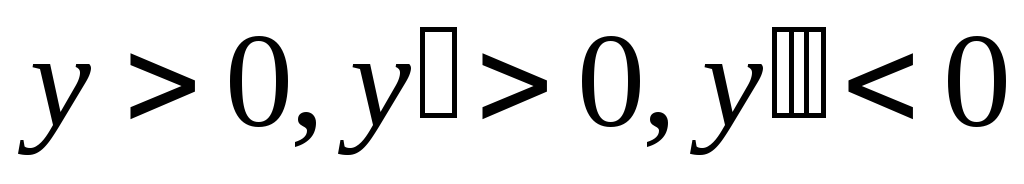 , ,
2)
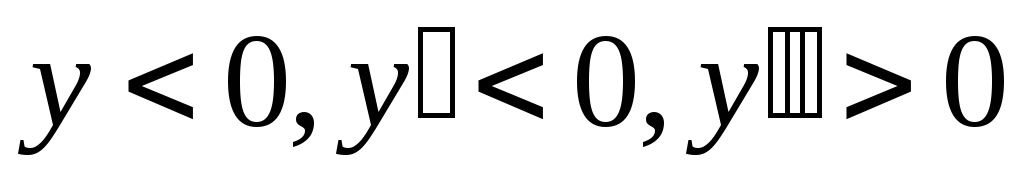 , ,
3)
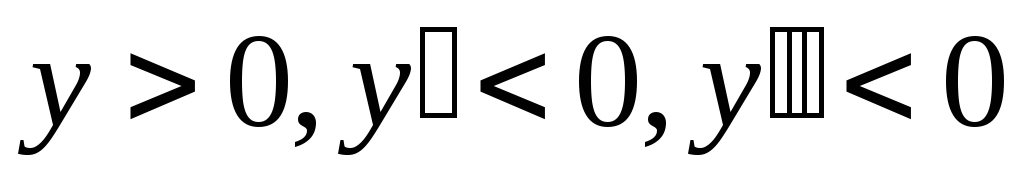 , ,
4)
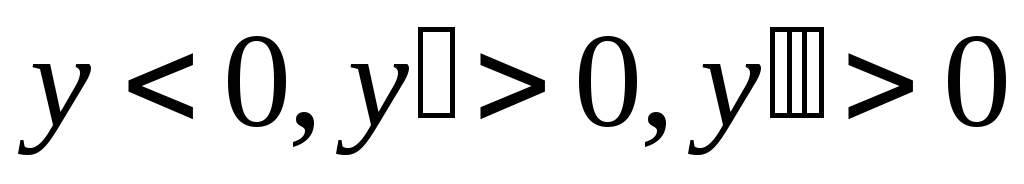 . .
Варианты
ответов:
A)
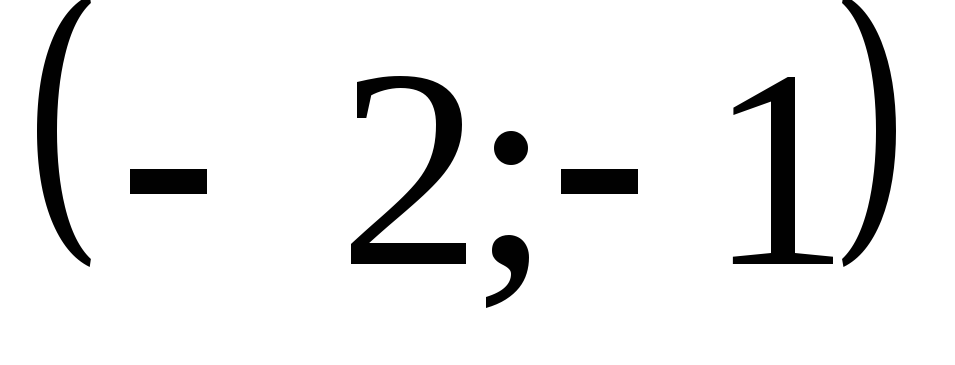 ,
B) ,
B)
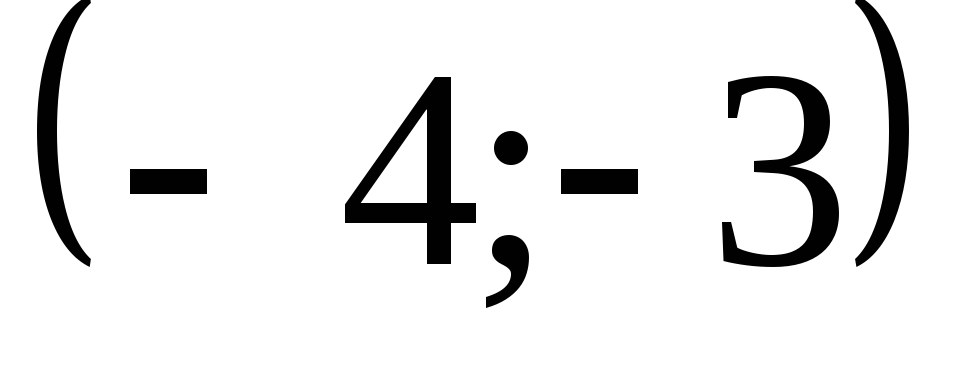 ,
C) ,
C)
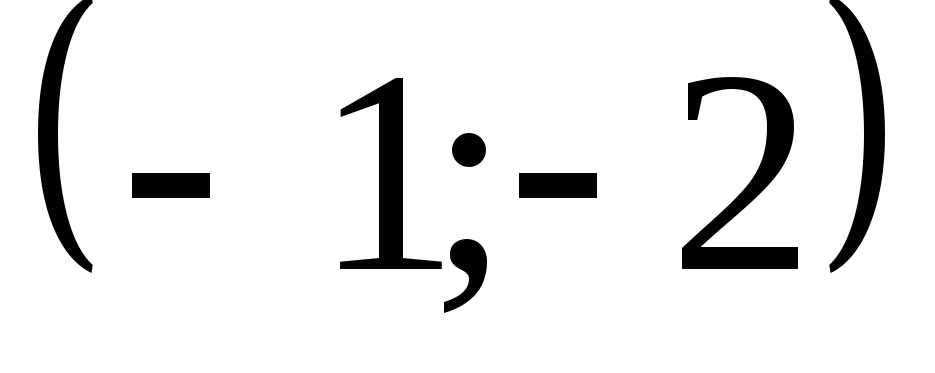 ,
D) ,
D)
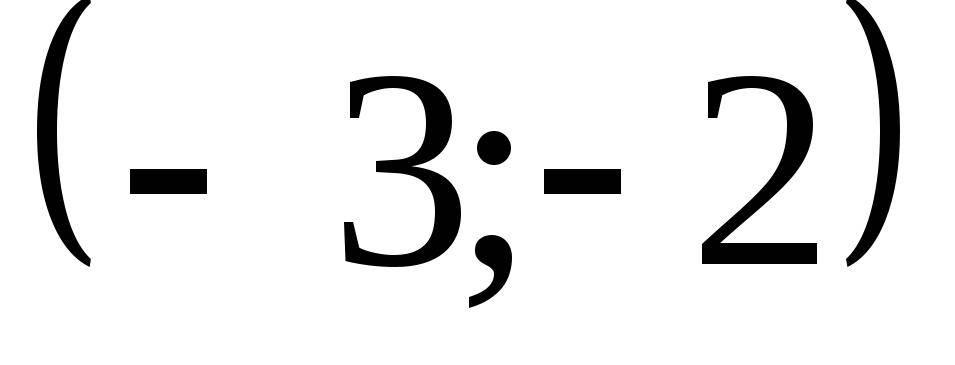 ,
E) ,
E)
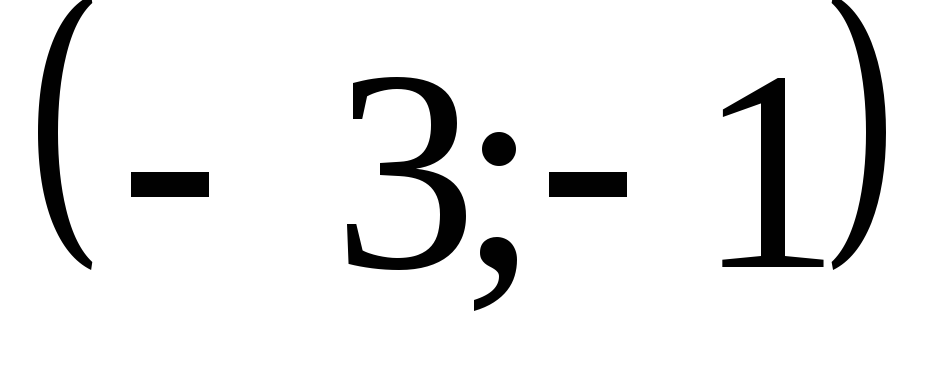 . .
Ответ:
1. A,
2. A,
2. B,
3. B,
3. C,
4. C,
4. D. D.
ЗАДАНИЕ
N 13
(-
выберите несколько вариантов
ответа)
(I.
стр.109)
Для
функции
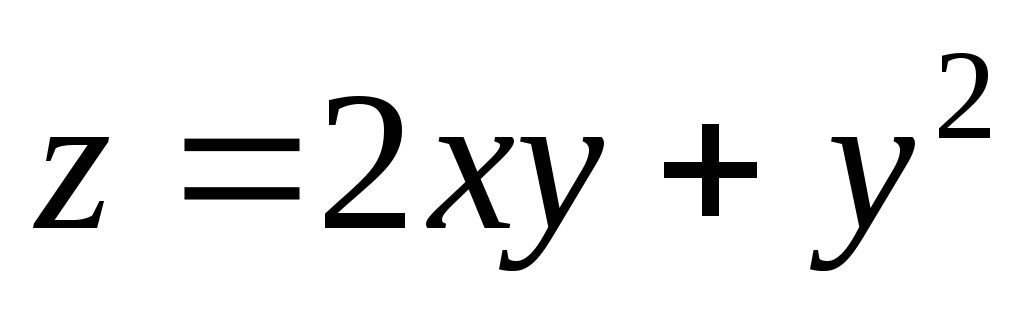 справедливы
соотношения … справедливы
соотношения …
Варианты
ответов:
1)
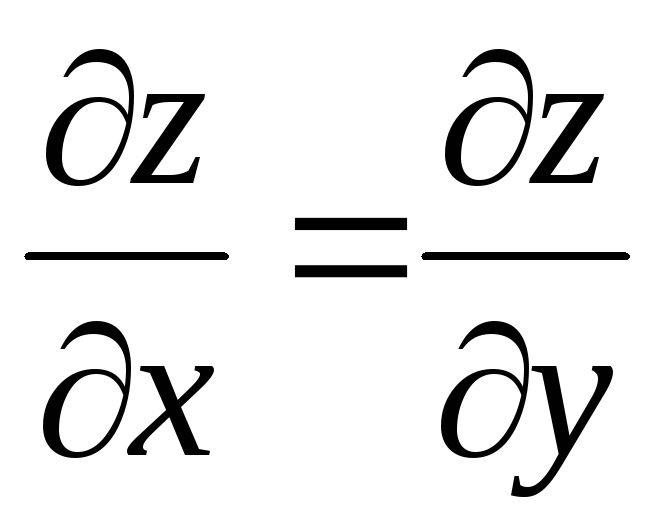 ,
2) ,
2)
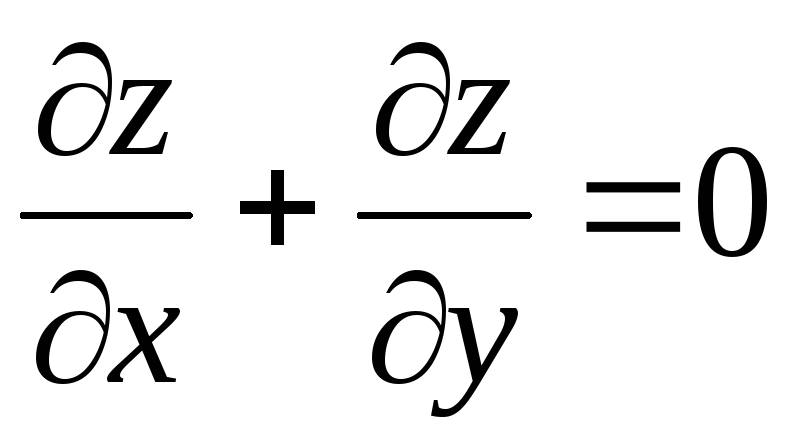 ,
3) ,
3)
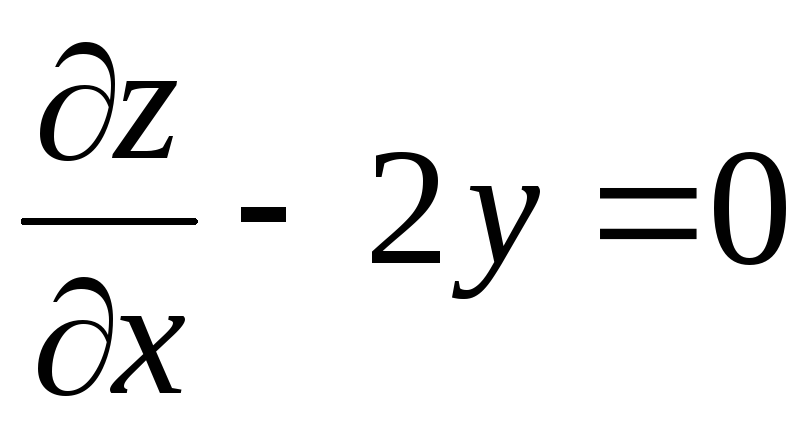 ,
4) ,
4)
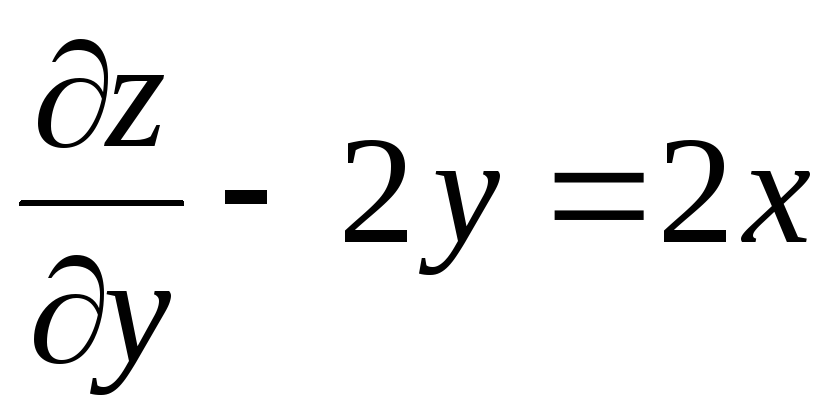 . .
Решение:
Найдем
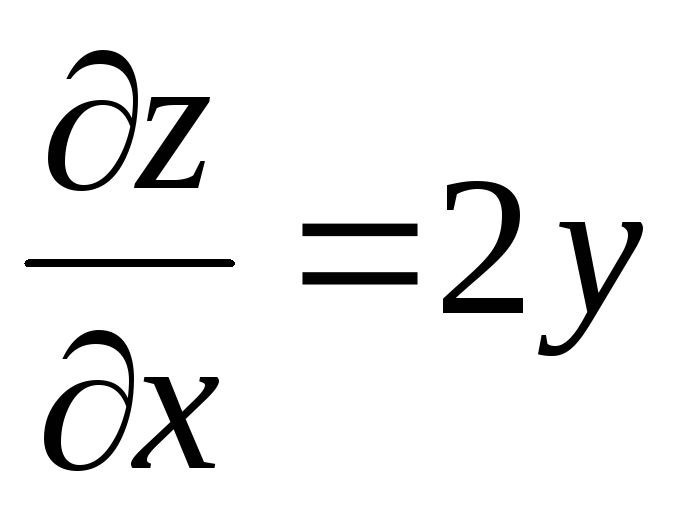 , ,
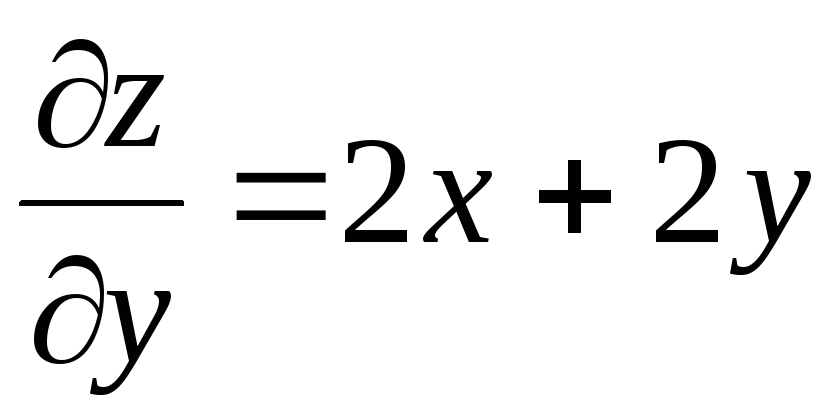 . .
Ответ:
3), 4).
ЗАДАНИЕ
N 14
(-
выберите варианты согласно тексту
задания)
(I.
стр.82)
Установите
соответствие между неопределенными
интегралами и разложениями
подынтегральных функций на
элементарные дроби.
1)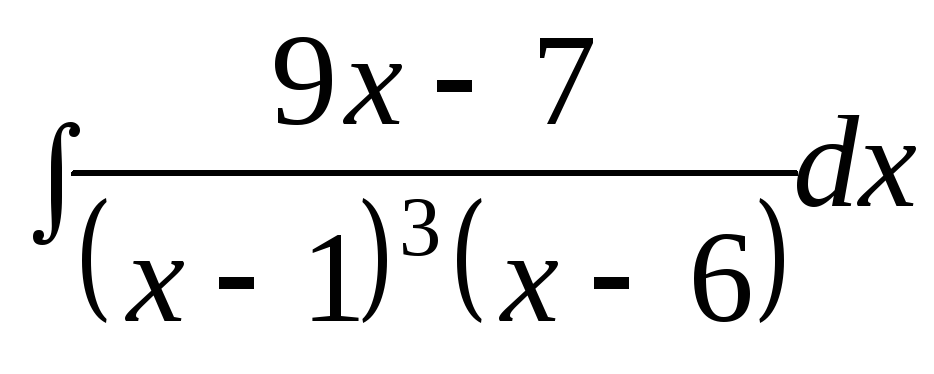 ,
2) ,
2)
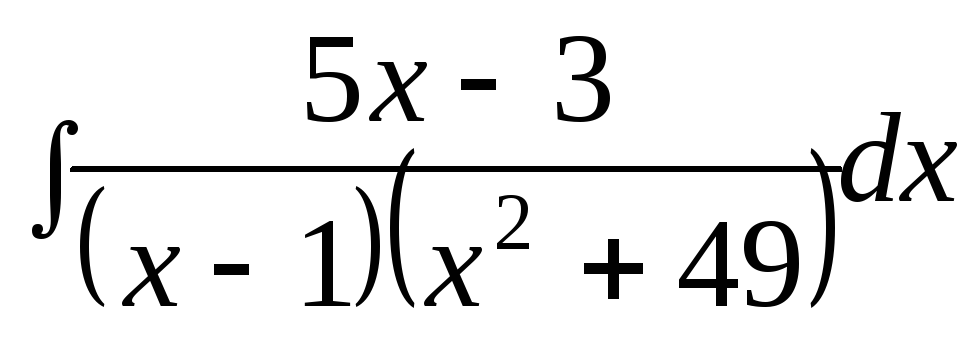 ,
3) ,
3)
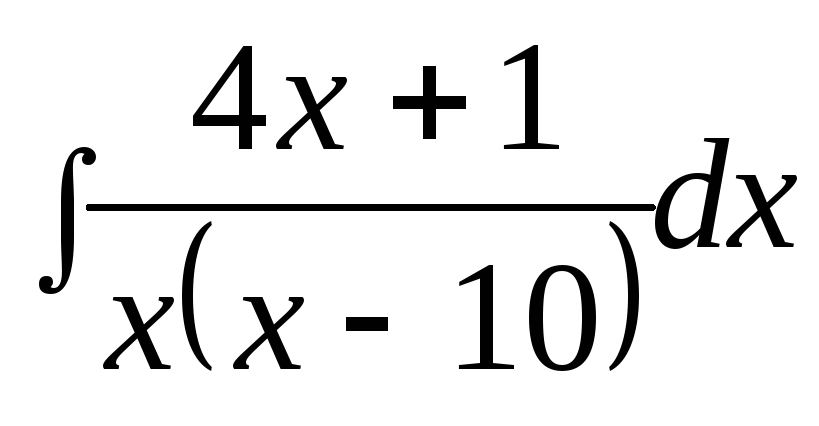 ,
4) ,
4)
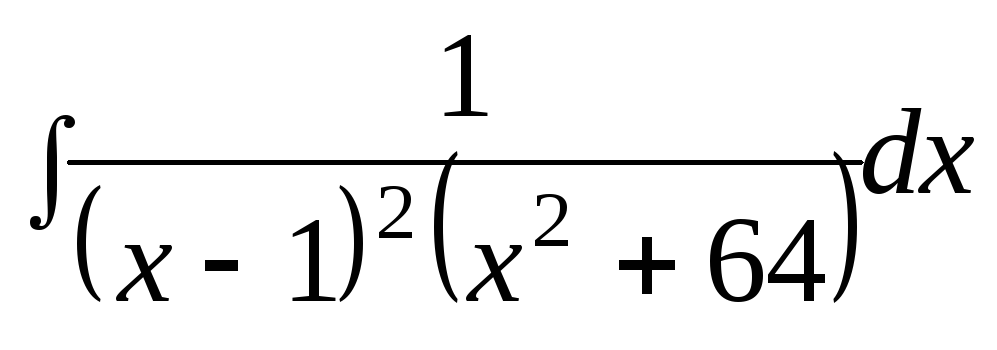 . .
Варианты
ответов:
A)
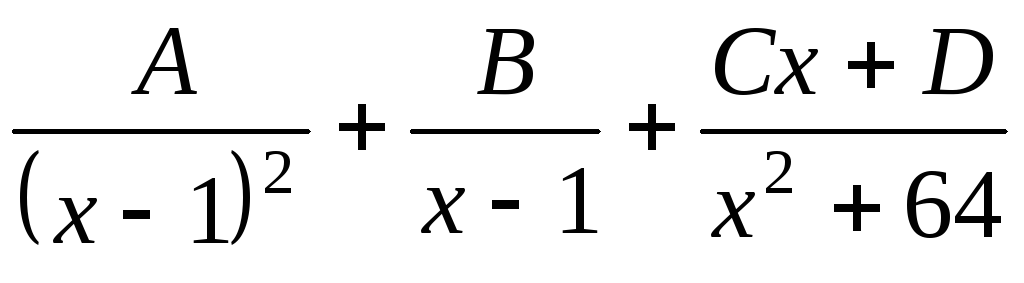 ,
B) ,
B)
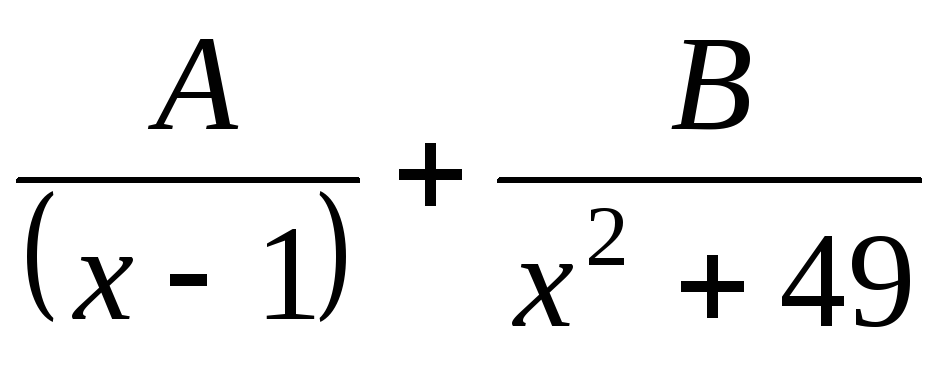 ,
C) ,
C)
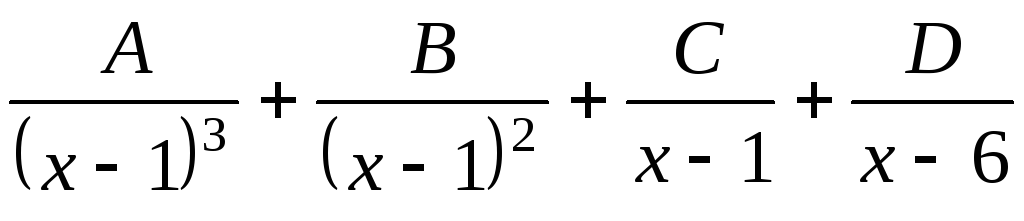 ,
D) ,
D)
 ,
E) ,
E)
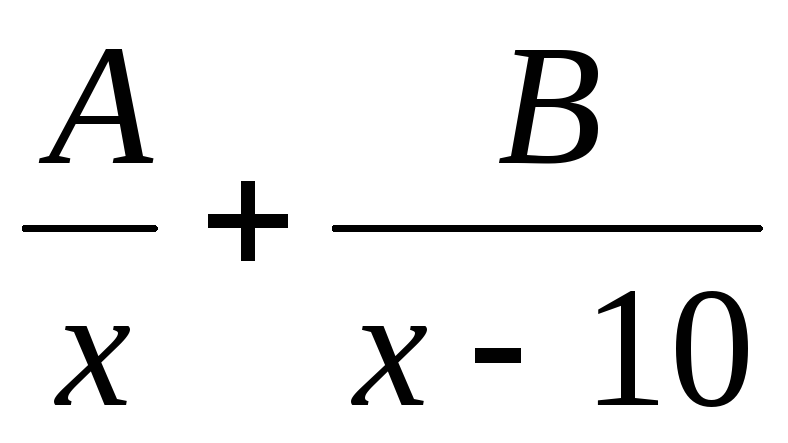 . .
Ответ:
1. C,
2. C,
2. D,
3. D,
3. E,
4. E,
4. A. A.
ЗАДАНИЕ
N 15
(-
введите ответ)
(I.
стр.87)
Если
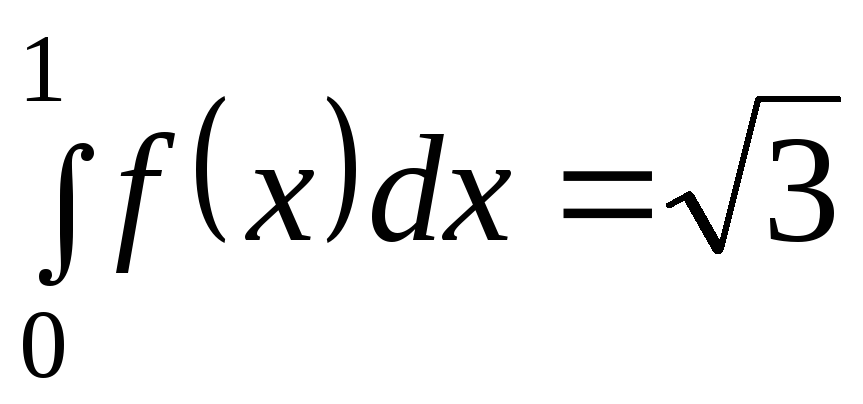 , ,
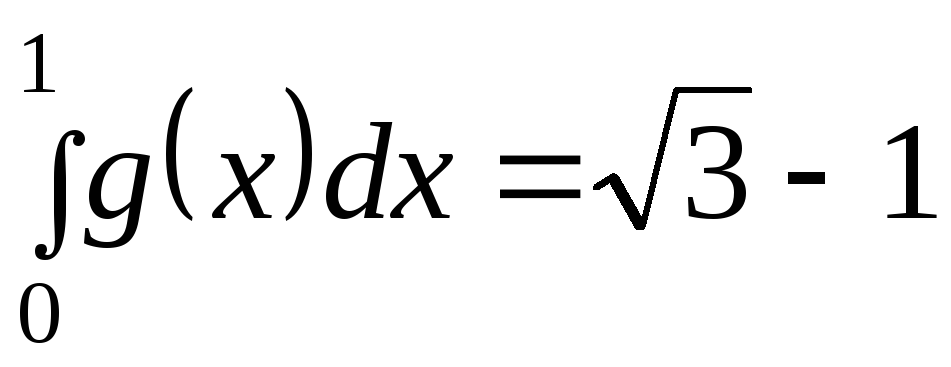 ,
то интеграл ,
то интеграл
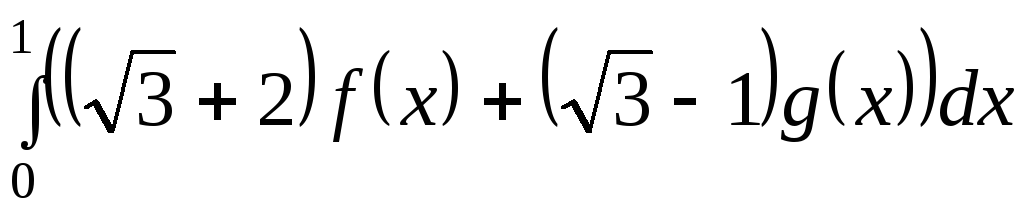 равен …
равен …
Решение:
Найдем
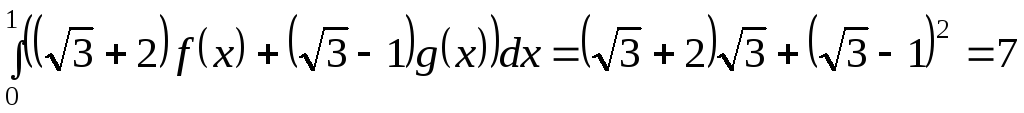
Ответ:
7
ЗАДАНИЕ
N 16
(-
выберите варианты согласно тексту
задания)
(I.
стр.89)
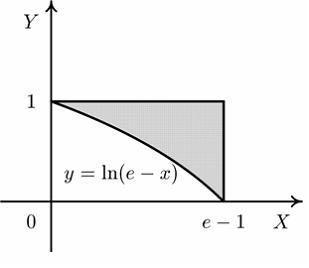
Установите
соответствие между заштрихованными
фигурами и определенными
интегралами, которые выражают
площади этих фигур.
1.
2.
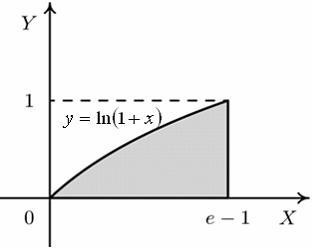
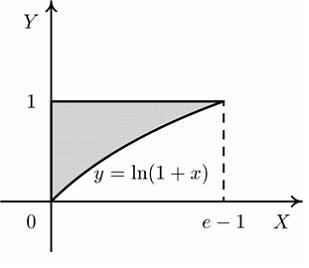
3.
4.

Варианты
ответов:
A)
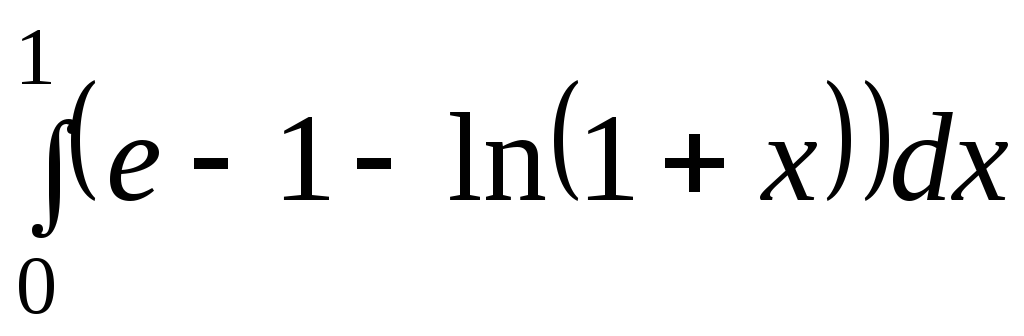 ,
B) ,
B)
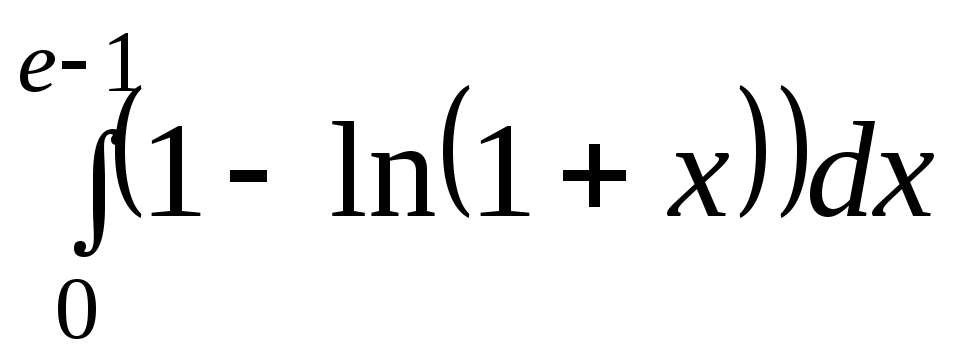 ,
C) ,
C)
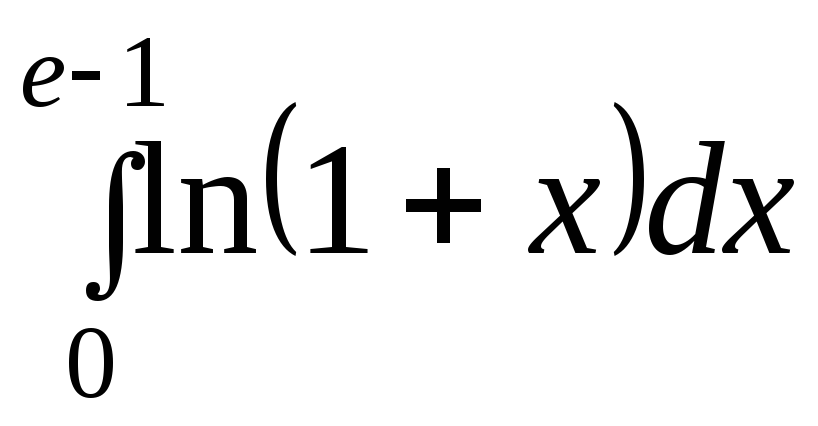 ,
D) ,
D)
 ,
E) ,
E)
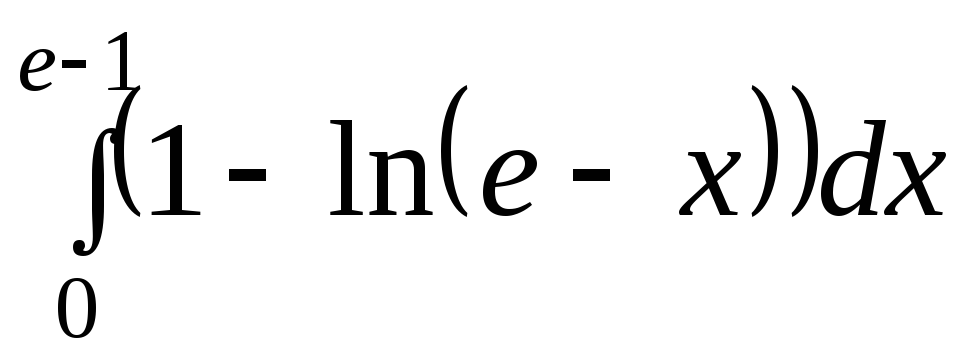 ,
F) ,
F)
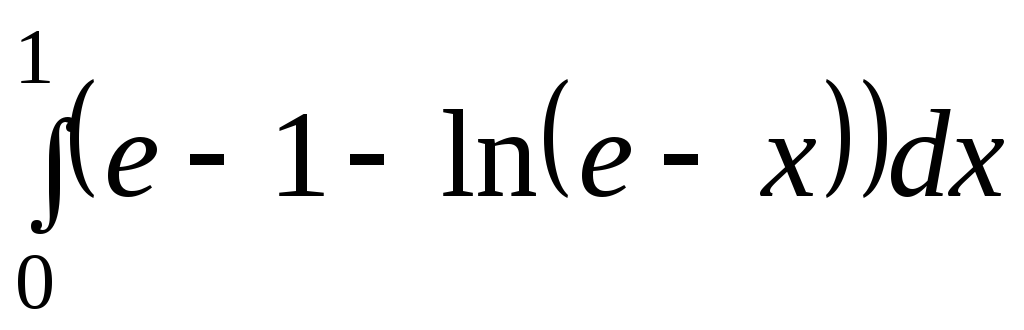 . .
Ответ:
1. C,
2. C,
2. B,
3. B,
3. D,
4. D,
4. E. E.
ЗАДАНИЕ
N 17
(-
выберите несколько вариантов
ответа)
(I.
стр.147,
154)
Бросают
2 кубика. События А – «на первом
кубике выпала тройка» и В – «на
втором кубике выпала шестерка»
являются:
Варианты
ответов:
1)
совместными,
2)
независимыми,
3)
зависимыми,
4)
несовместными.
Ответ:
1), 2).
ЗАДАНИЕ
N 18
(-
выберите несколько вариантов
ответа)
(I.
стр.148, 154)
Несовместные
события
 , ,
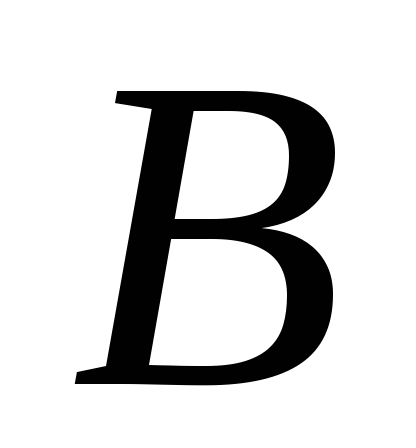 и и
 не
образуют
полную группу, если их вероятности
равны … не
образуют
полную группу, если их вероятности
равны …
Варианты
ответов:
1)
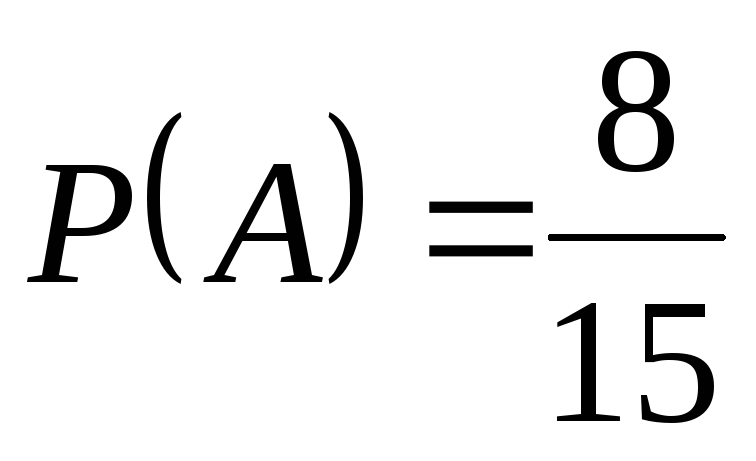 , ,
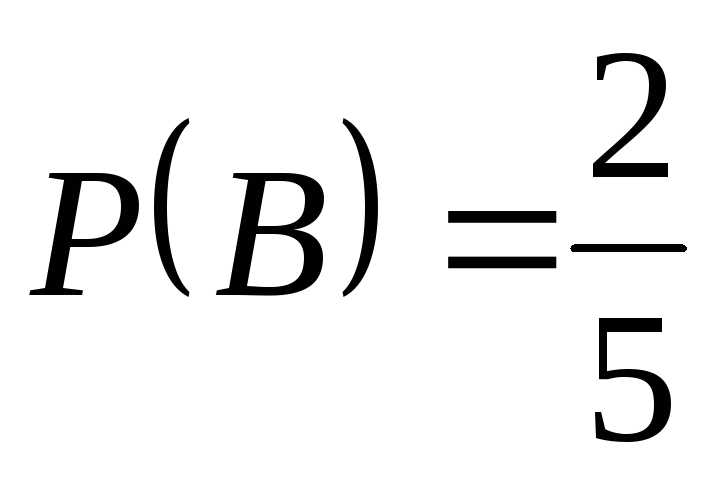 , ,
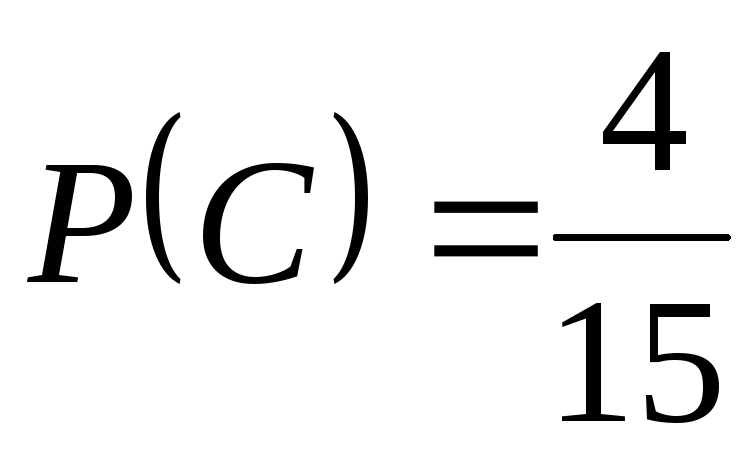 ,
2) ,
2)
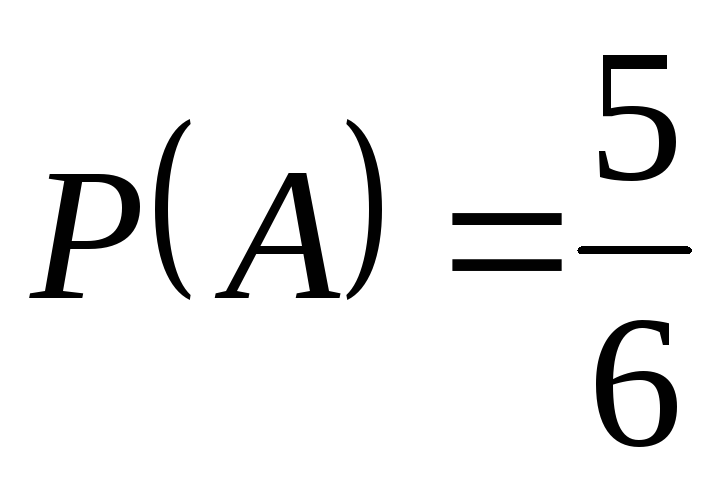 , ,
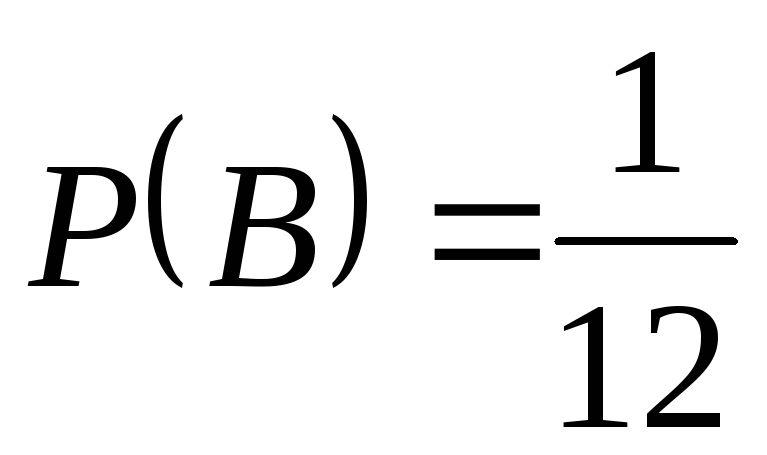 , ,
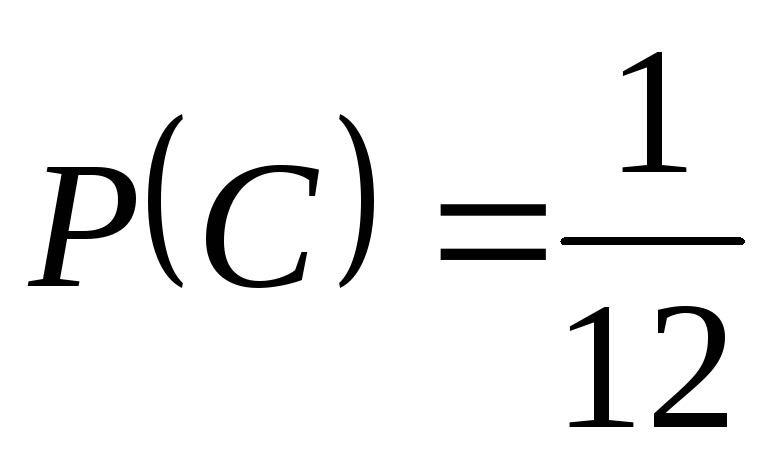 ,
3) ,
3)
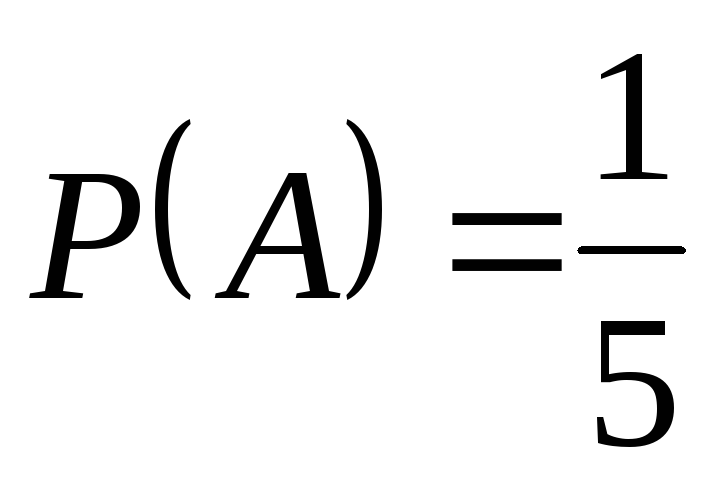 , ,
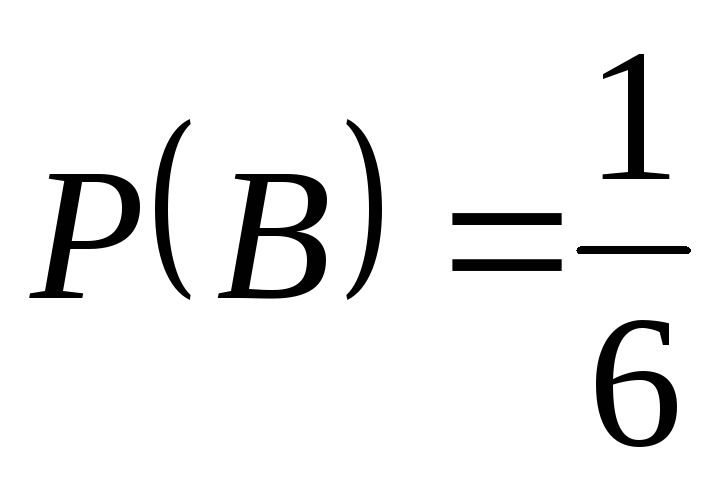 , ,
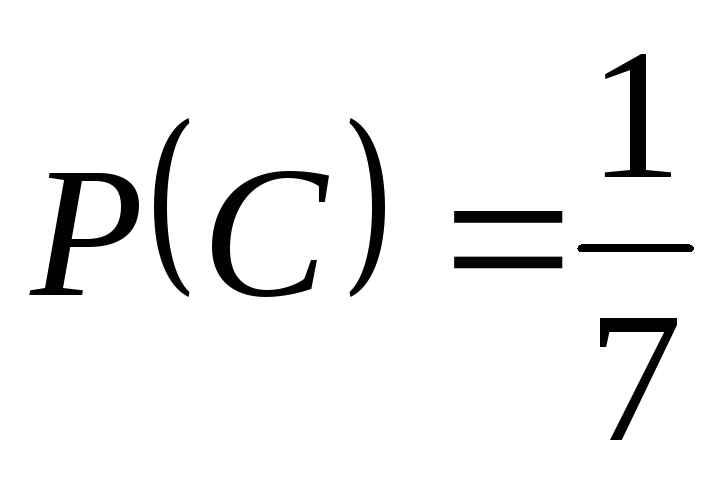 ,
4) ,
4)
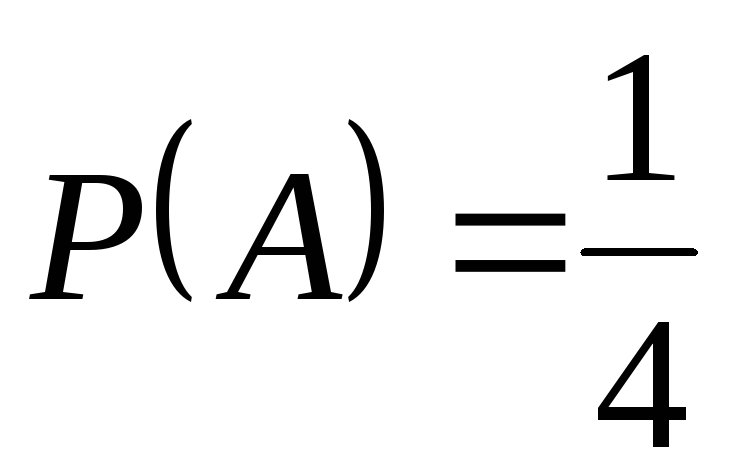 , ,
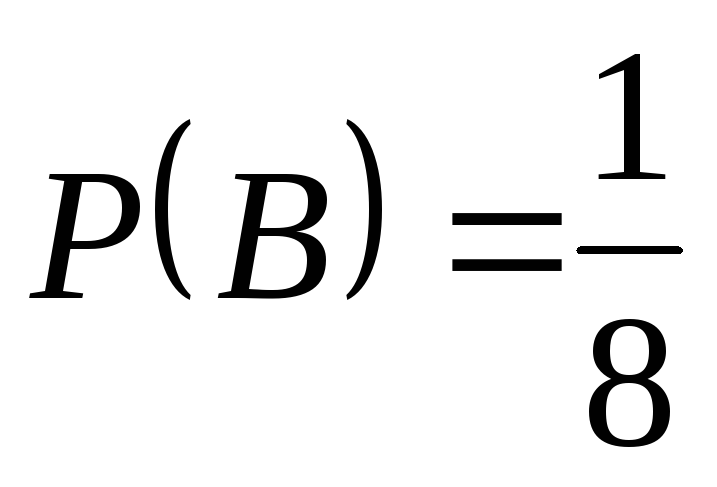 , ,
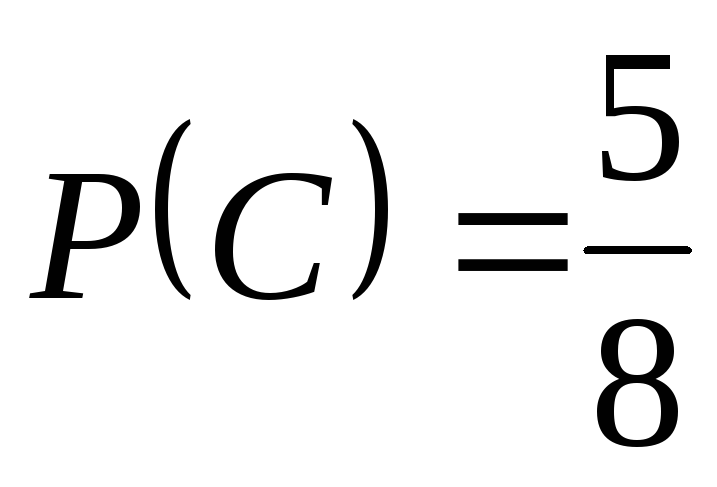 .
.
Решение:
Так как несовместные события
 , ,
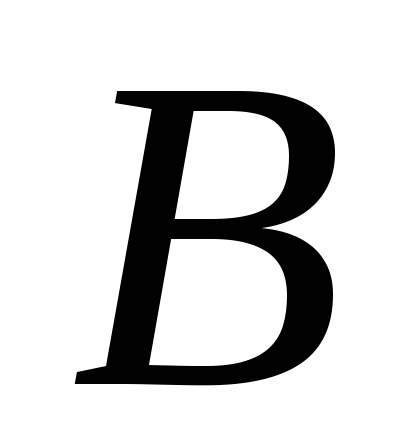 и и
 не
образуют
полную группу, то не
образуют
полную группу, то
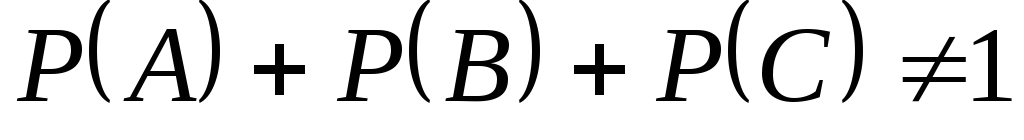 . .
Ответ:
1), 3).
ЗАДАНИЕ
N 19
(-
выберите один вариант ответа)
(I.
стр.156)
Событие
А
может наступить лишь при условии
появления одного из двух
несовместных событий
 и и
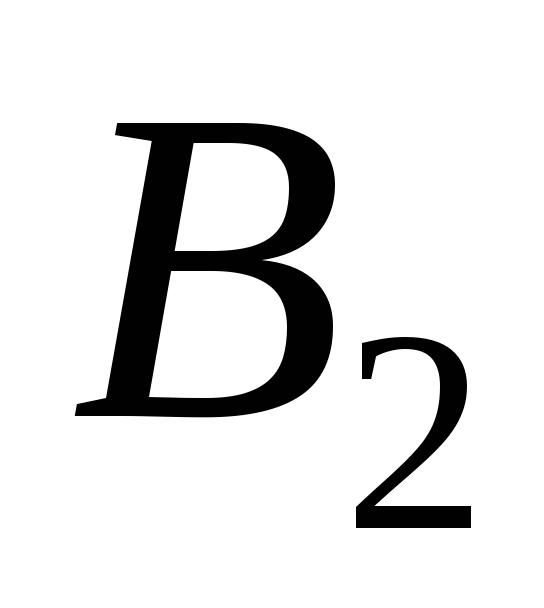 ,
образующих полную группу событий.
Известны вероятность ,
образующих полную группу событий.
Известны вероятность
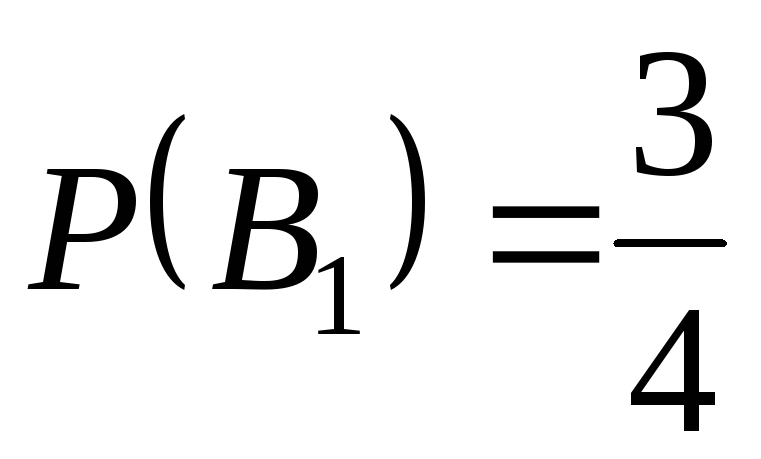 и
условные вероятности и
условные вероятности
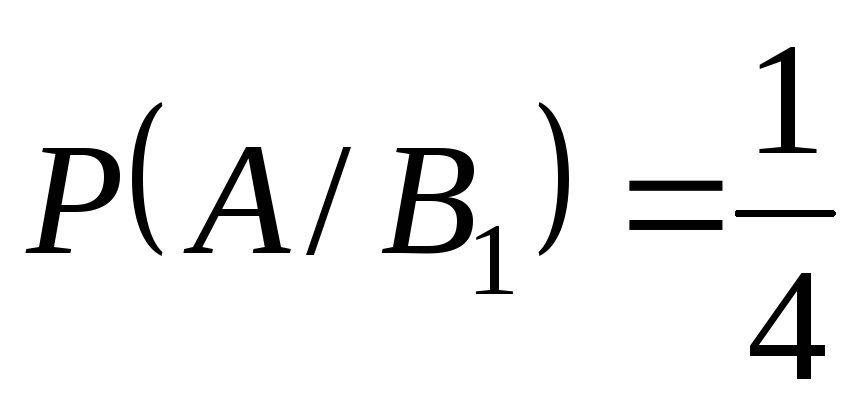 , ,
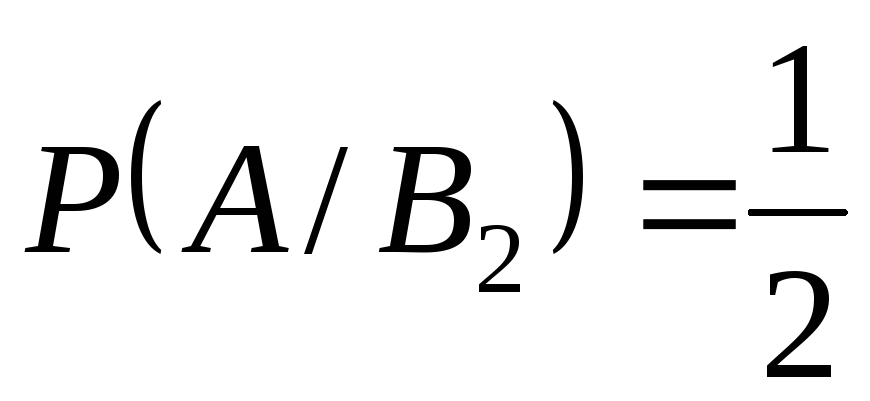 .
Тогда вероятность .
Тогда вероятность
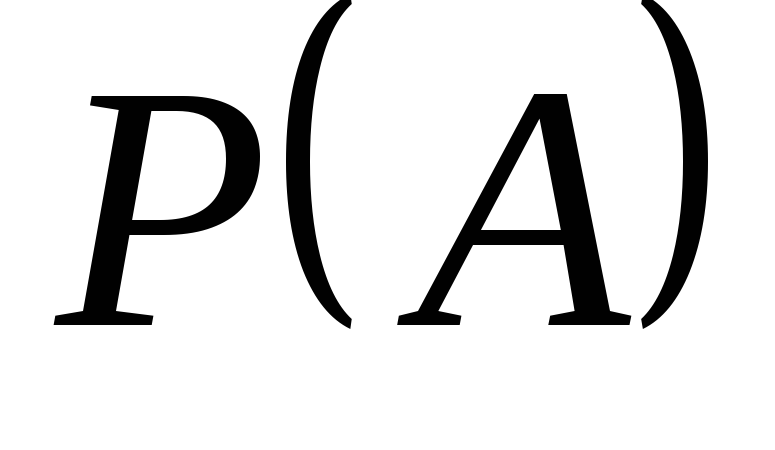 равна
… равна
…
Варианты
ответов:
1)
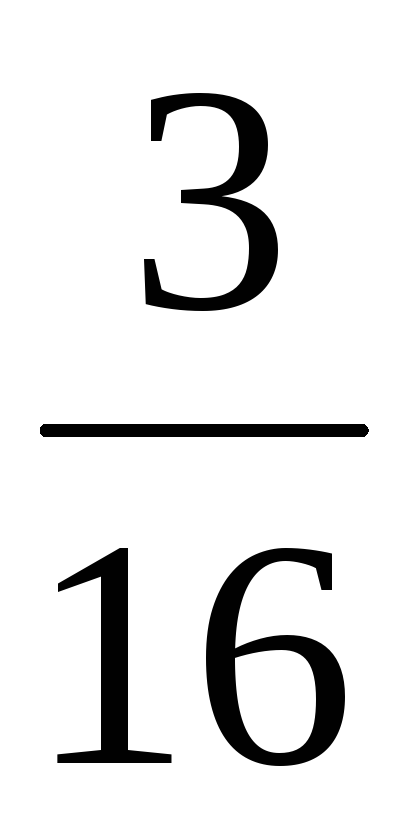 ,
2) ,
2)
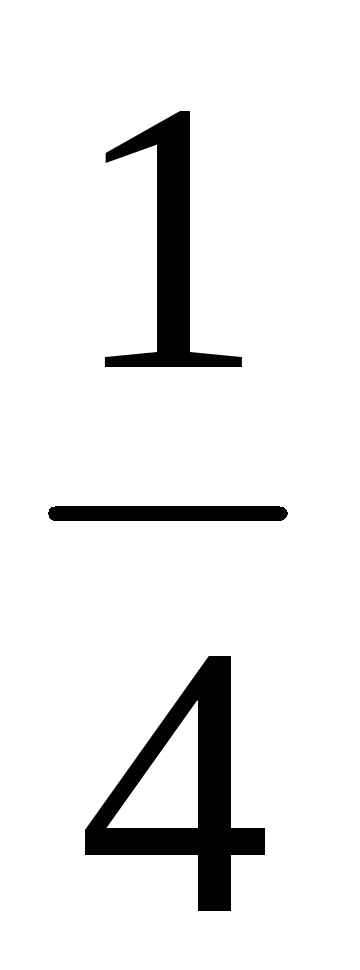 ,
3) ,
3)
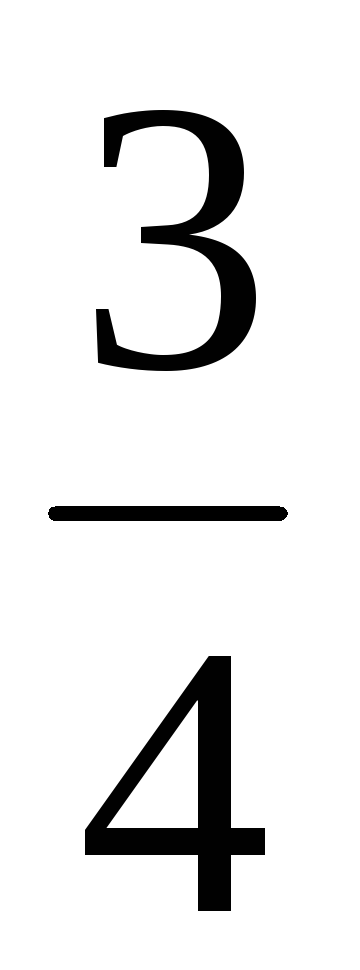 ,
4) ,
4)
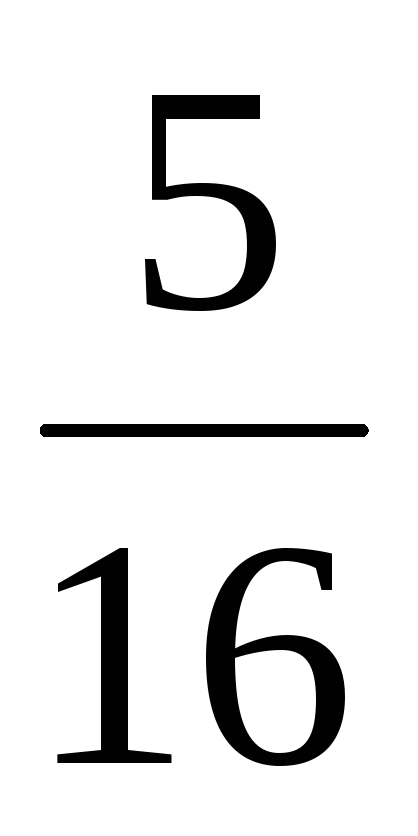 . .
Решение:
Так как несовместные события
 и и
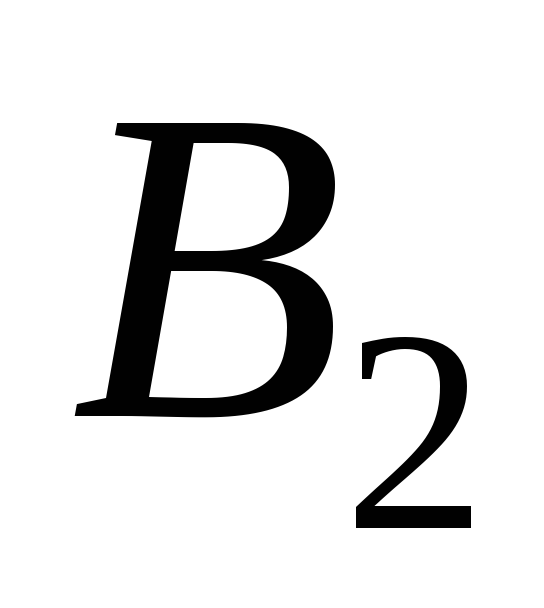 ,
образуют полную группу собы-тий,
то ,
образуют полную группу собы-тий,
то
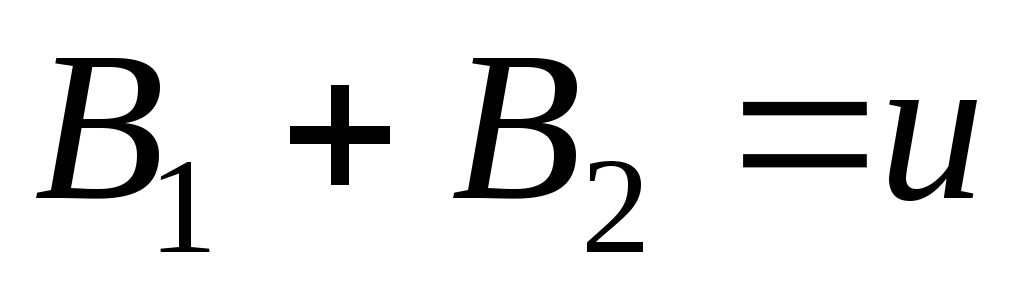 , ,
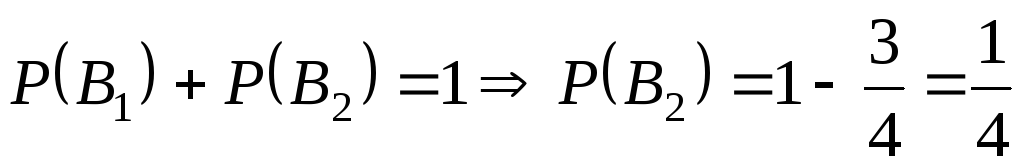 .
По формуле полной вероятности
получим .
По формуле полной вероятности
получим
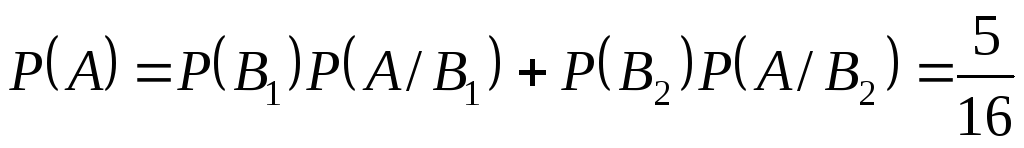 . .
Ответ:
4)
ЗАДАНИЕ
N 20
(-
выберите один вариант ответа)
(II.
стр.6)
По
выборке объема n=100 построена
гистограмма частот:
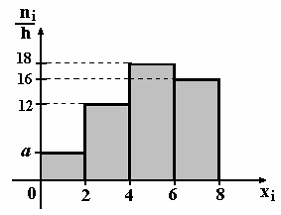
Тогда
значение а
равно…
Варианты
ответов:
1)
4,
2) 3,
3) 5,
4) 54.
Решение:
Из графика найдем длину интервала
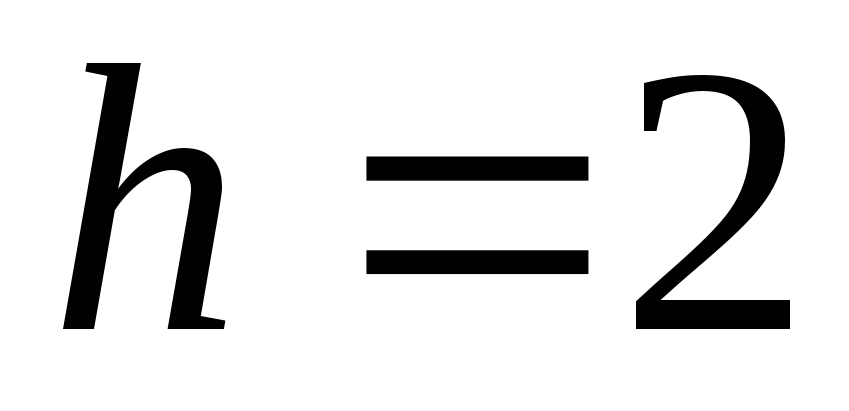 ,
при этом ,
при этом
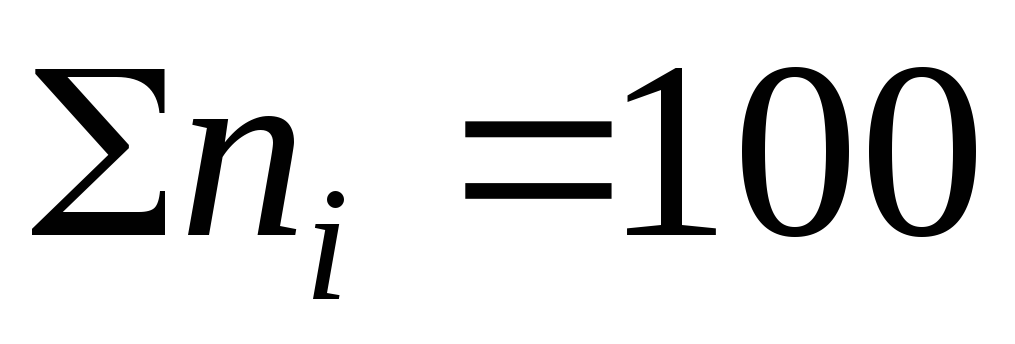 .
Из графи-ка найдем .
Из графи-ка найдем
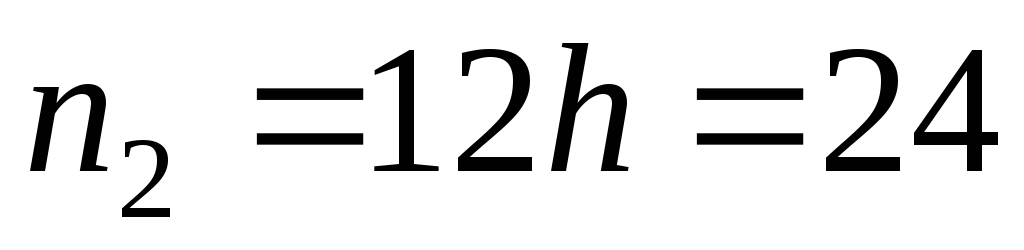 , ,
 , ,
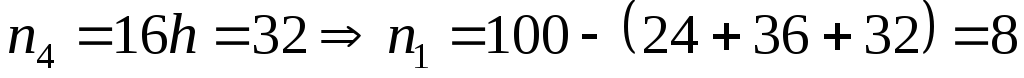 .
Найдем .
Найдем
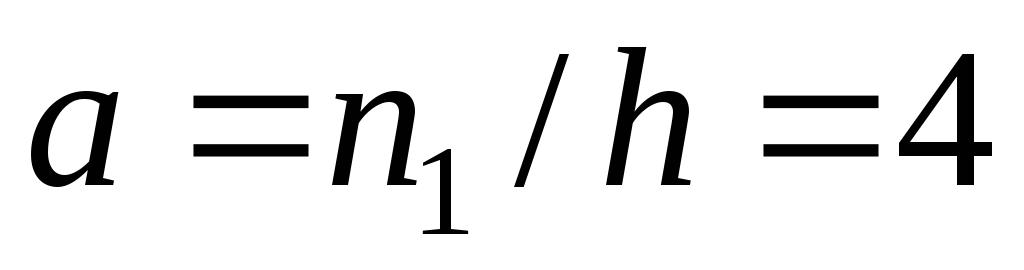 . .
Ответ:
1)
ЗАДАНИЕ
N 21
(-
выберите один вариант ответа)
(II.
стр.8)
Мода
вариационного ряда 3 , 4 , 5 , 6 , 10 ,
10 , 12 равна …
Варианты
ответов:
1)
3,
2) 10,
3) 12,
4) 6.
Ответ:
2)
ЗАДАНИЕ
N 22
(-
выберите один вариант ответа)
(II.
стр.7)
Дана
выборка объема n.
Если каждый элемент выборки
уменьшить в 4 раза, то выбо-рочное
среднее
 … …
Варианты
ответов:
1)
увеличится в 4 раза,
2) уменьшится
в 2 раза,
3) не
изменится
,
4)
уменьшится
в 4 раза.
Решение:
По условию задачи
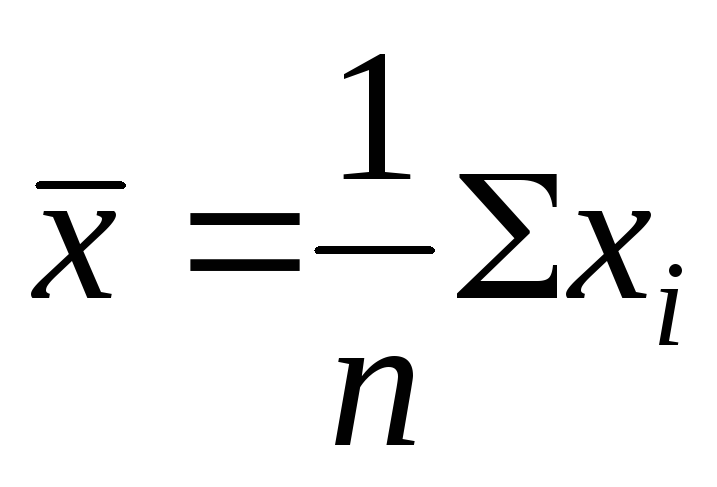 ,
сделаем замену ,
сделаем замену
 .
Получим .
Получим
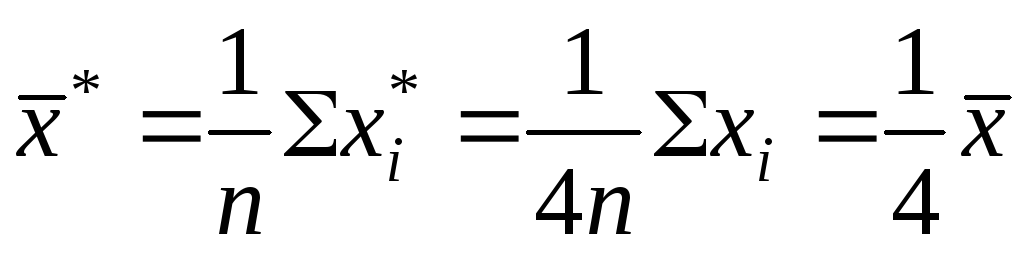 . .
Ответ:
4)
ЗАДАНИЕ
N 23
(-
введите ответ)
(II.
стр.43)
Максимальное
значение функции
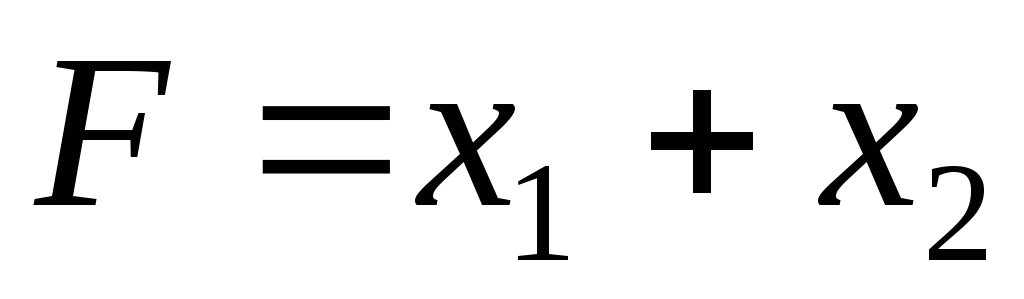 при
ограничениях при
ограничениях
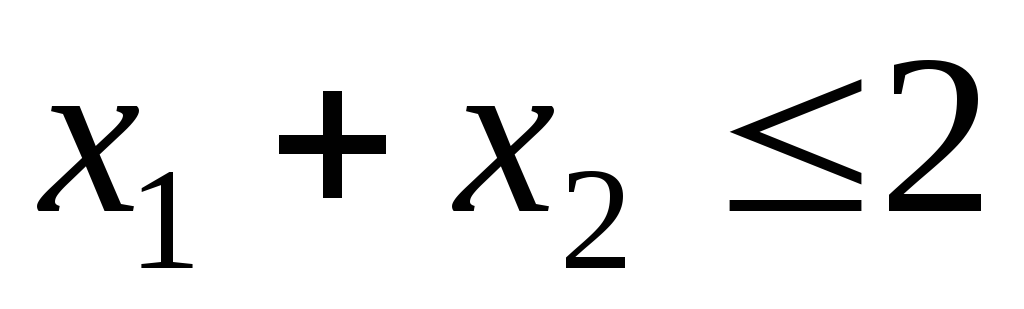 , ,
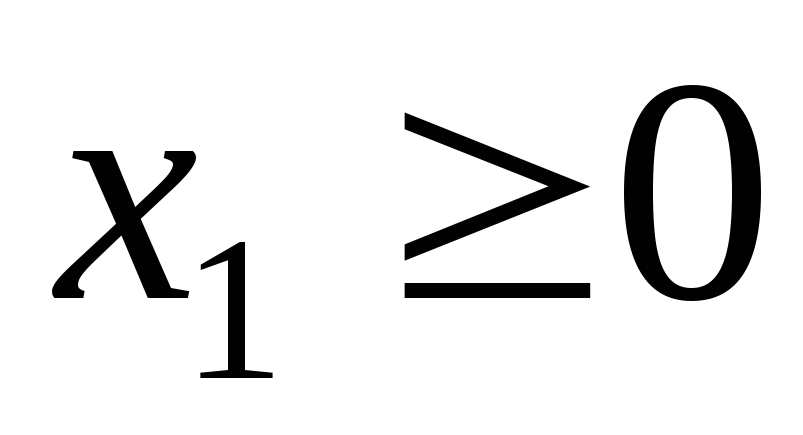 , ,
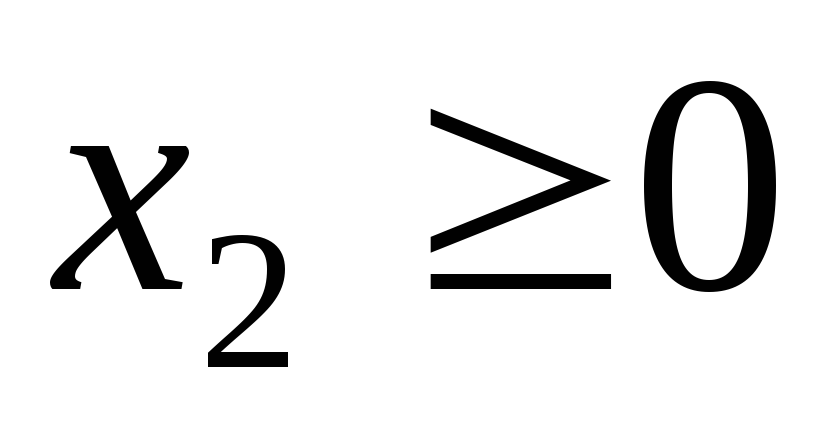 равно
… равно
…
Решение:
Определим прямые
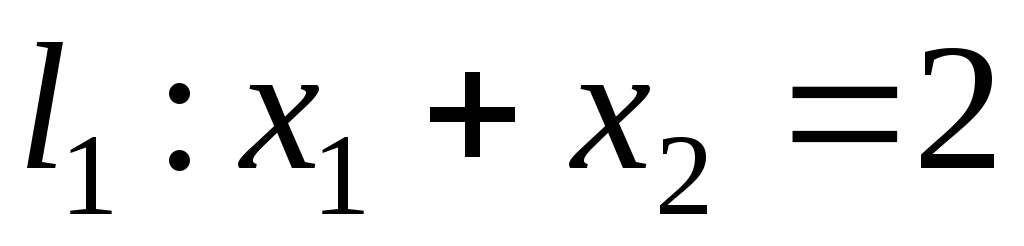 , ,
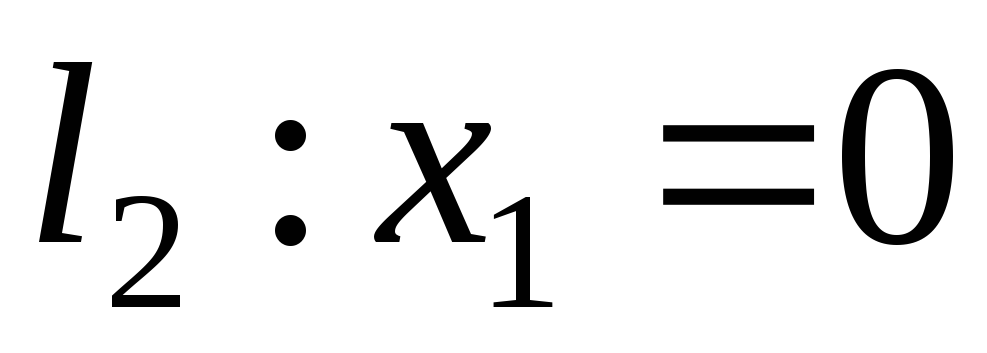 , ,
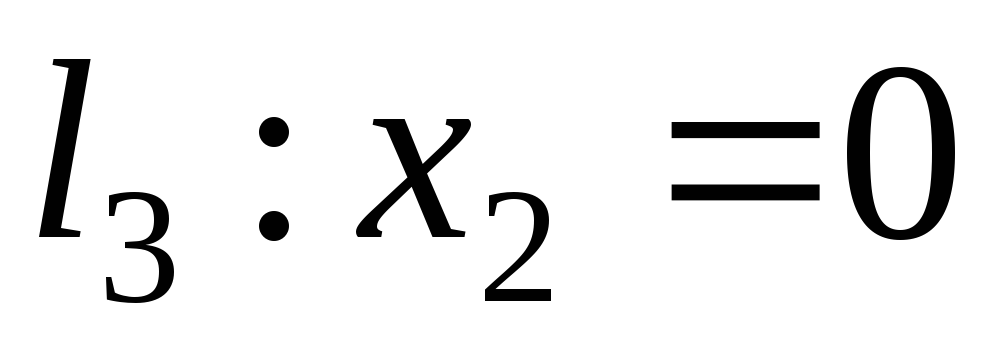 .
Найдем точки пересечения прямых .
Найдем точки пересечения прямых
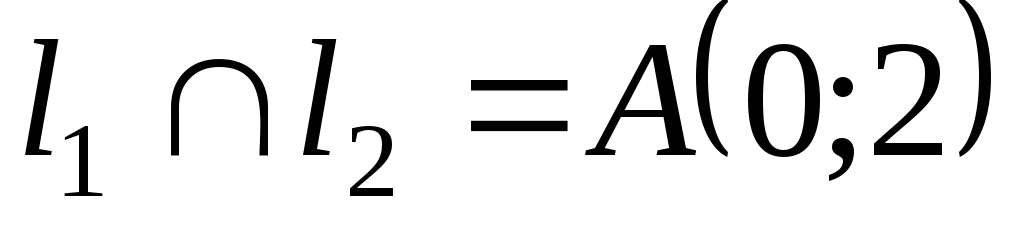 , ,
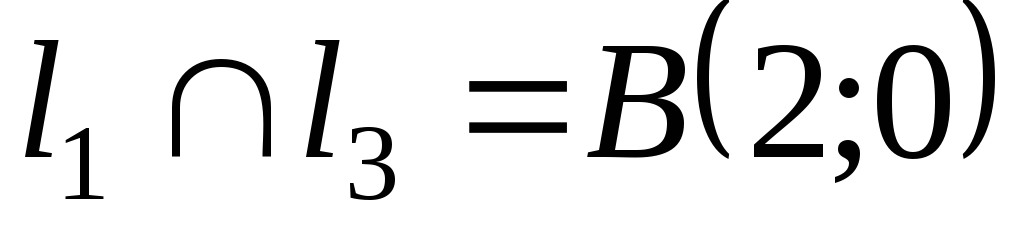 , ,
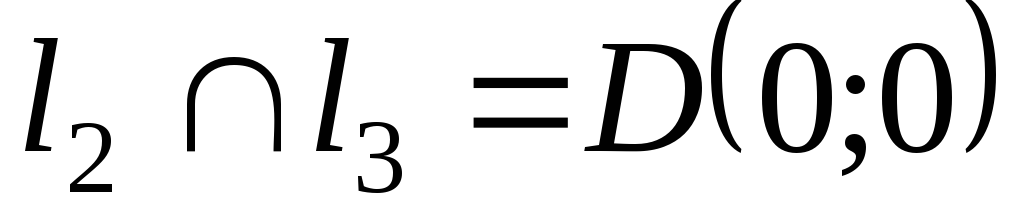 и значения
функции
и значения
функции
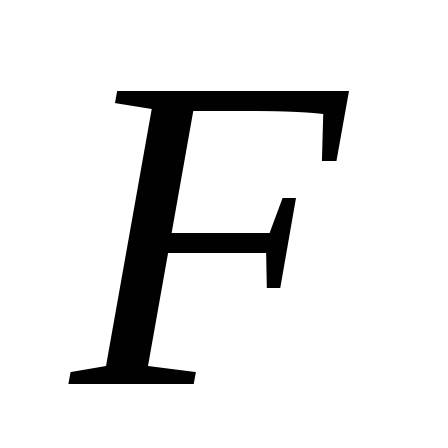 в полученных точках
в полученных точках
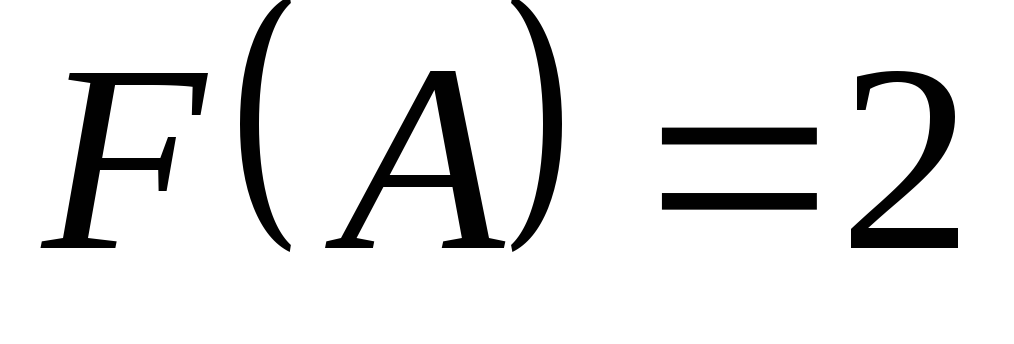 , ,
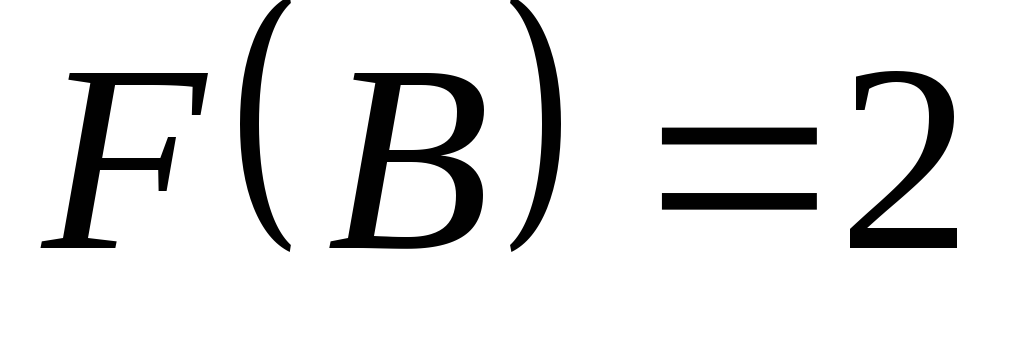 , ,
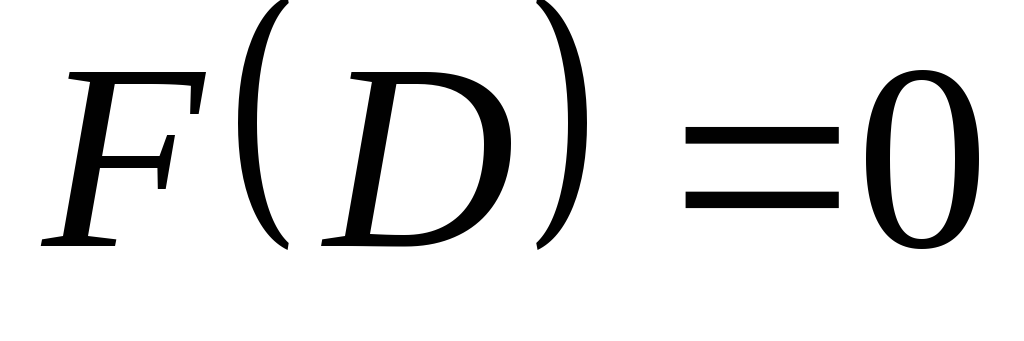 . .
Ответ:
2
ЗАДАНИЕ
N 24
(-
выберите один вариант ответа)
(II.
стр.95)
Транспортная
задача
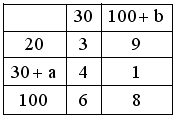
будет
закрытой, если …
Варианты
ответов:
1)
a=55, b=80,
2) a=55,
b=75,
3) a=55,
b=70,
4) a=55,
b=65.
Решение:
Из условий задачи находим
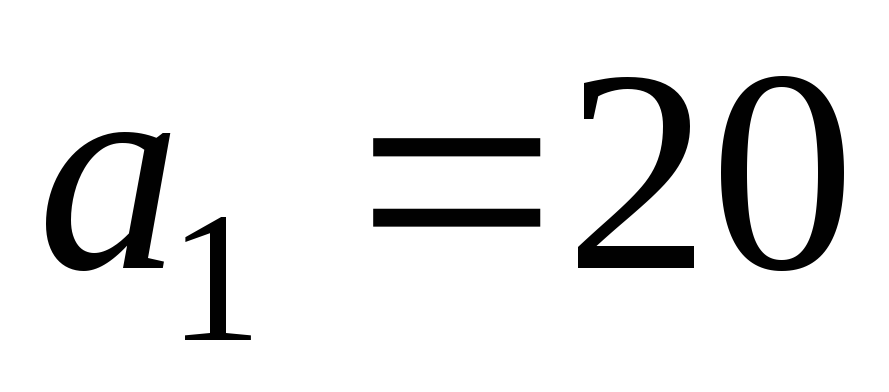 , ,
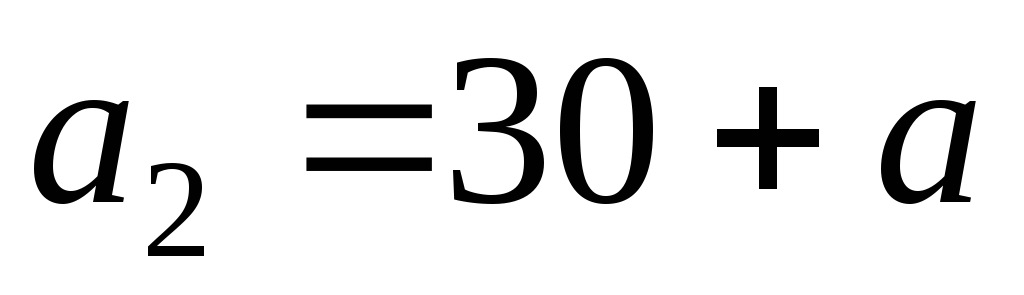 , ,
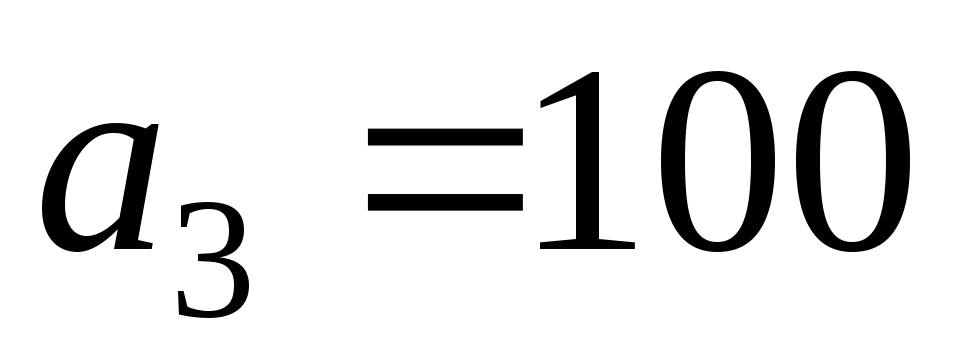 , ,
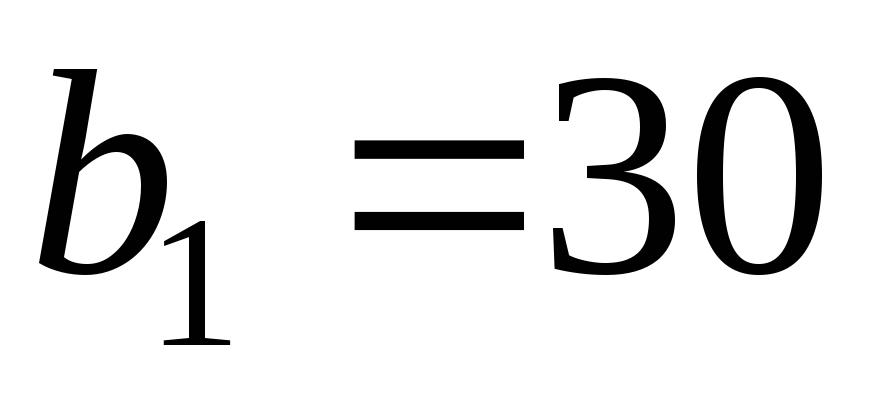 , ,
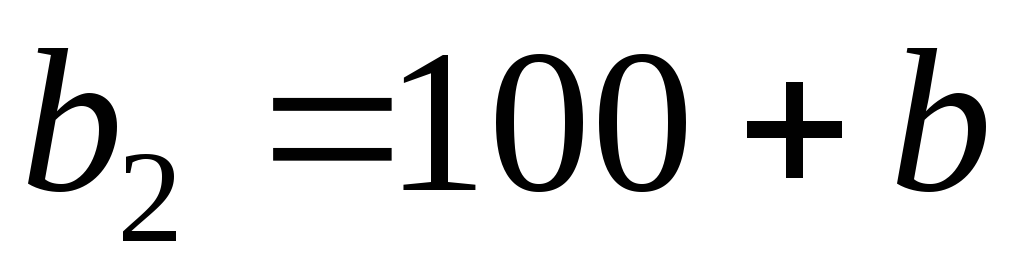 .
Транспортная задача называется
закрытой, если .
Транспортная задача называется
закрытой, если
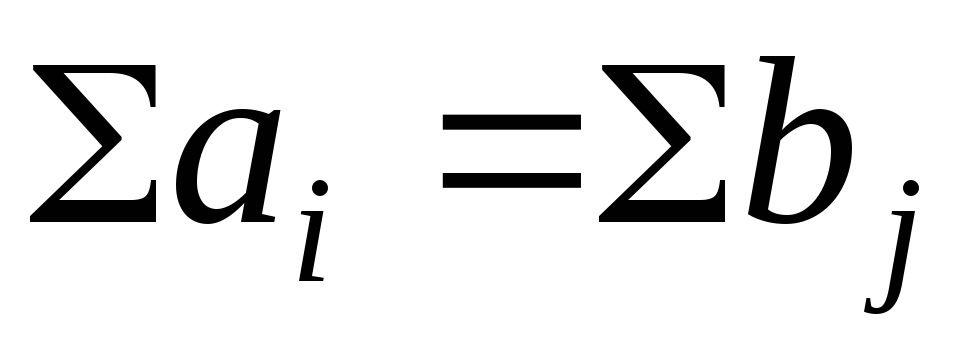 .
В задаче .
В задаче
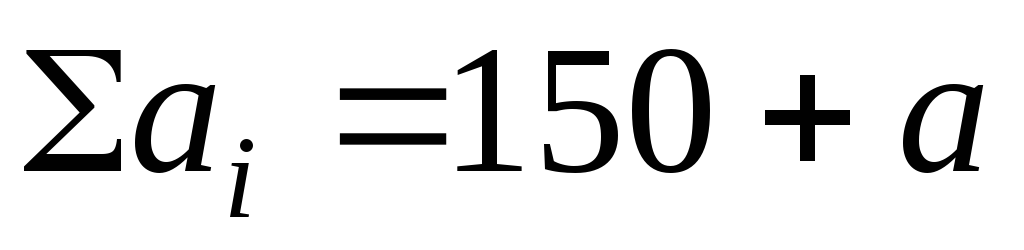 , ,
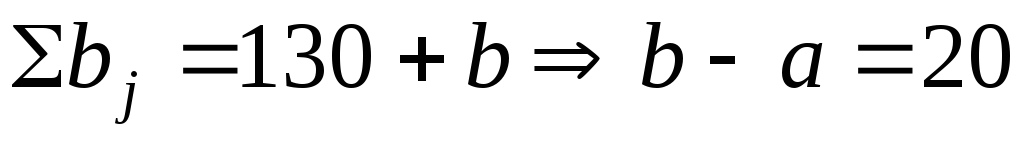 . .
Ответ:
2)
ЗАДАНИЕ
N 25
(-
выберите один вариант ответа)
(II.
стр.160, 162)
Для
сетевого графика, изображенного
на рисунке
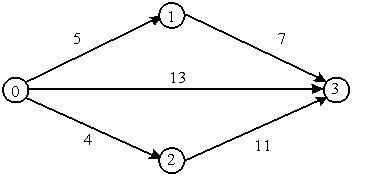
длина
критического пути равна…
Варианты
ответов:
1)
40,
2) 12,
3) 13,
4)
15.
Решение:
Наиболее протяженный путь по
времени называется критическим
путем. В задаче наиболее протяженным
является путь
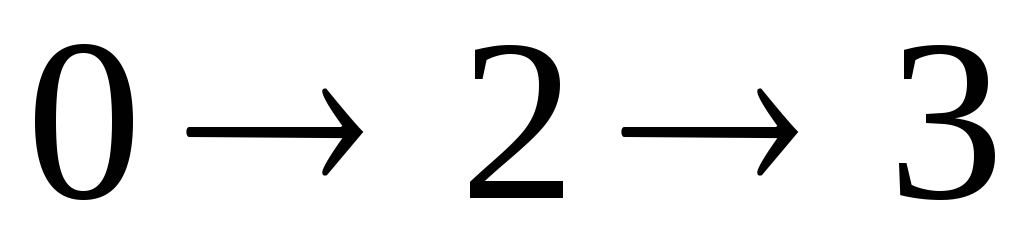 ,
его длина равна 4+11+15. ,
его длина равна 4+11+15.
Ответ:
4)
ЗАДАНИЕ
N 26
(-
выберите один вариант ответа)
(I.
стр.112)
Функция
полезности потребления имеет
вид
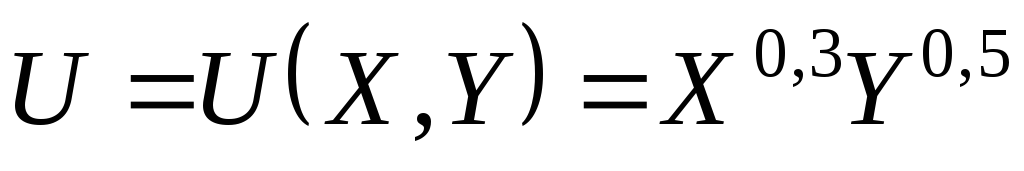 .
Тогда при .
Тогда при
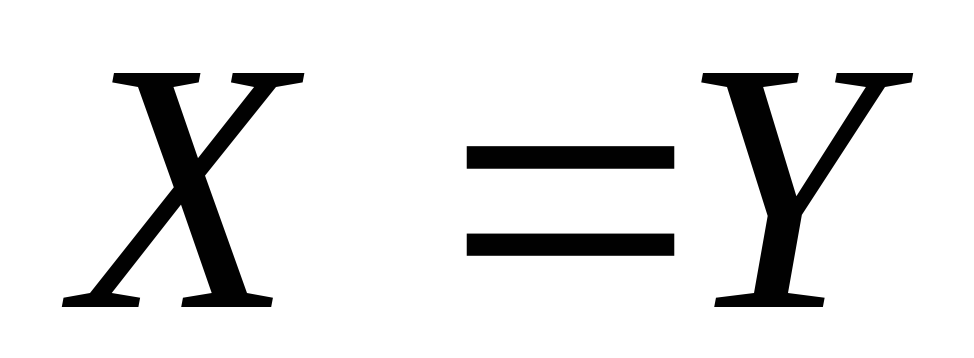 предельная
норма замещения продукта X
продуктом Y предельная
норма замещения продукта X
продуктом Y
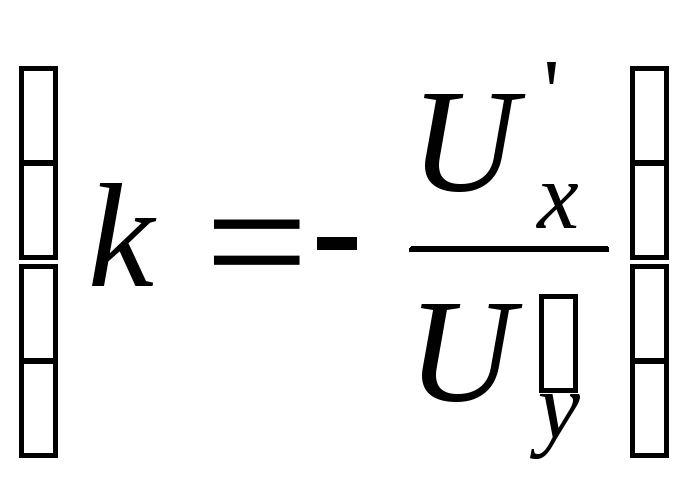 равна
… равна
…
Варианты
ответов:
1)
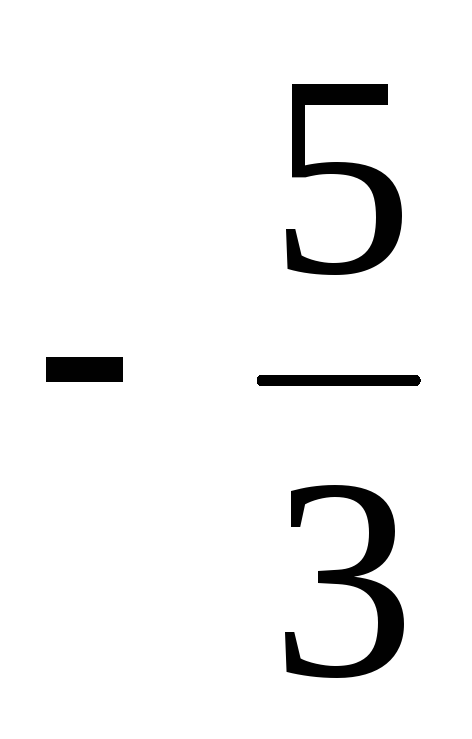 ,
2) ,
2)
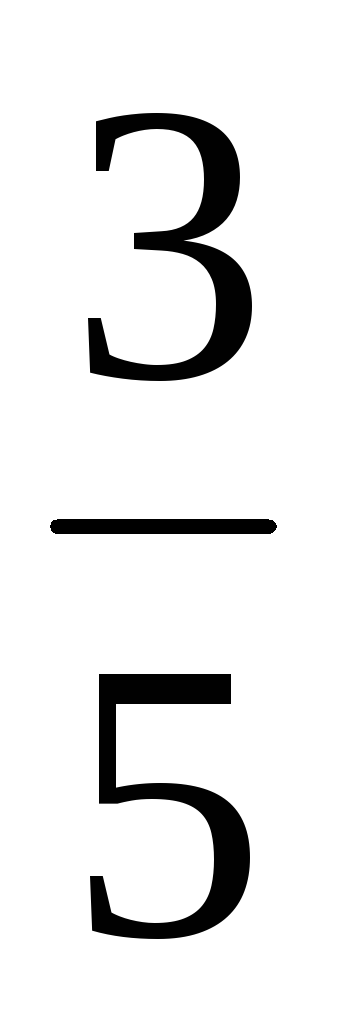 ,
3) ,
3)
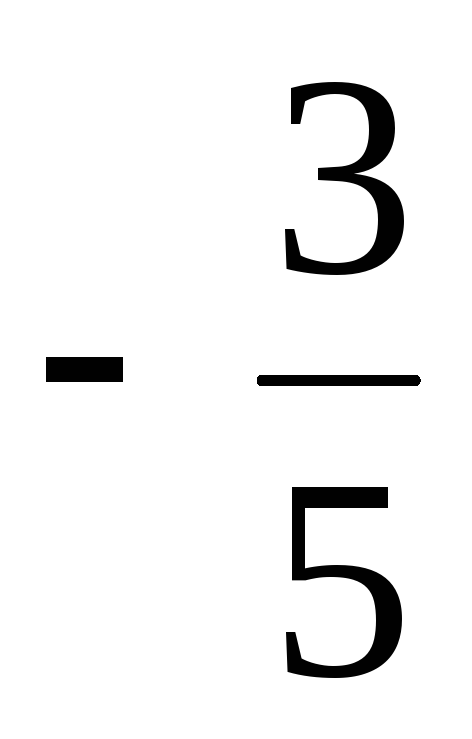 ,
4) ,
4)
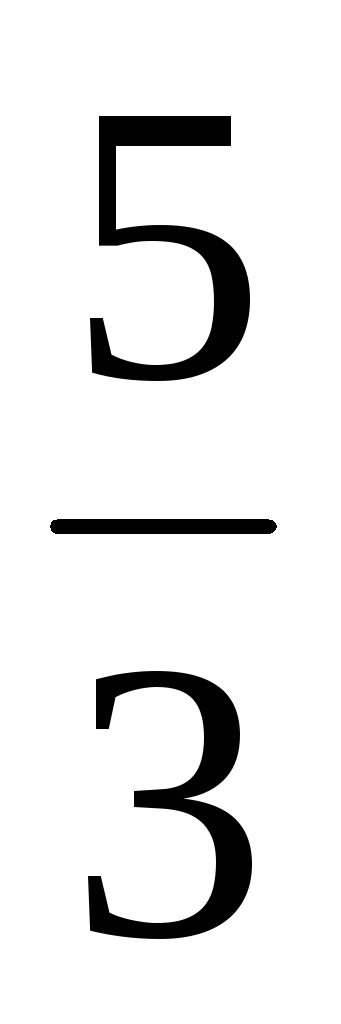 . .
Решение:
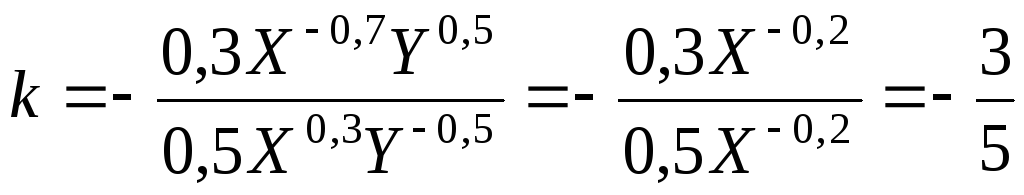 . .
Ответ:
3)
ЗАДАНИЕ
N 27
(-
выберите один вариант ответа)
(I.
стр.109)
Дана
функция полезности
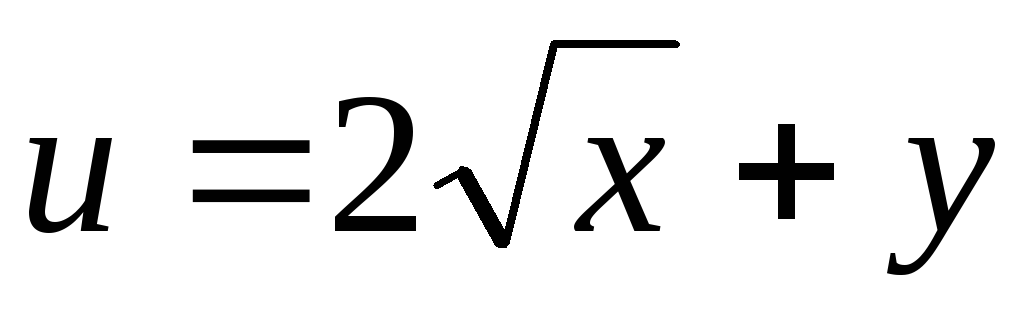 .
Тогда кривая безразличия задается
уравнением… .
Тогда кривая безразличия задается
уравнением…
Варианты
ответов:
1)
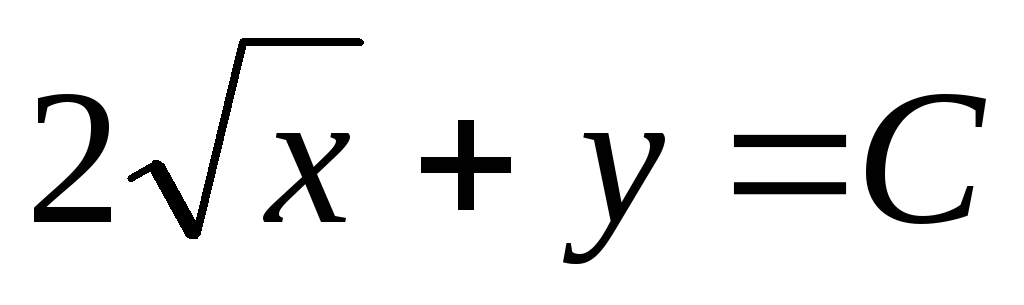 ,
2) ,
2)
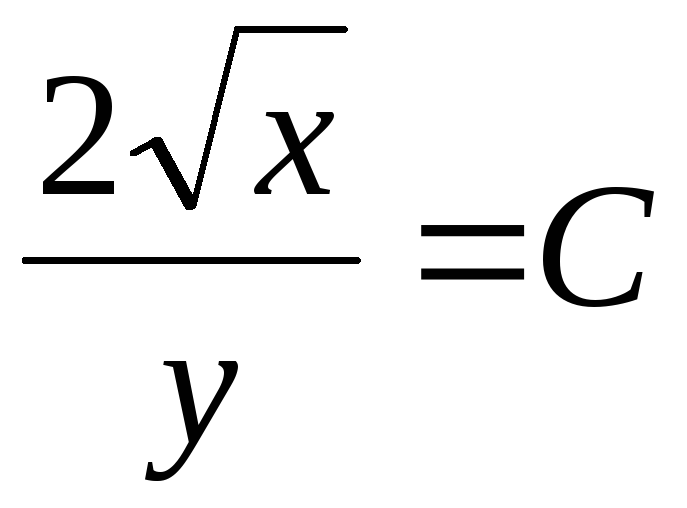 ,
3) ,
3)
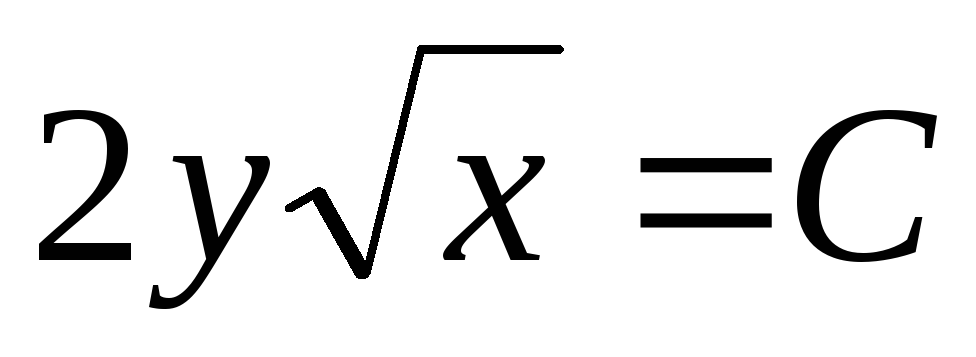 ,
4) ,
4)
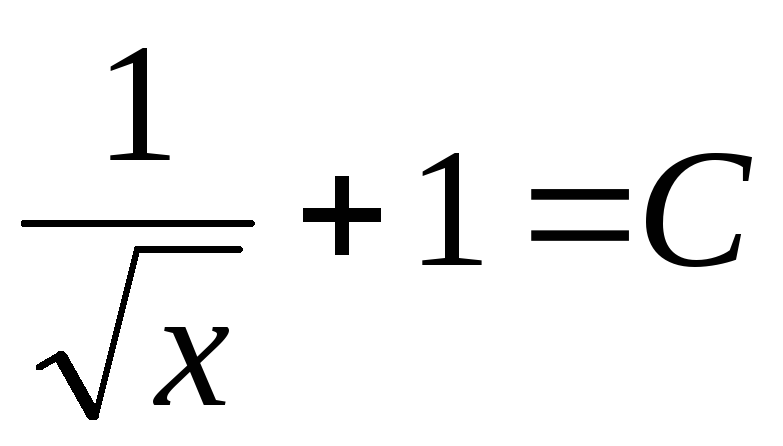 . .
Решение:
Кривая безразличия задается
уравнением
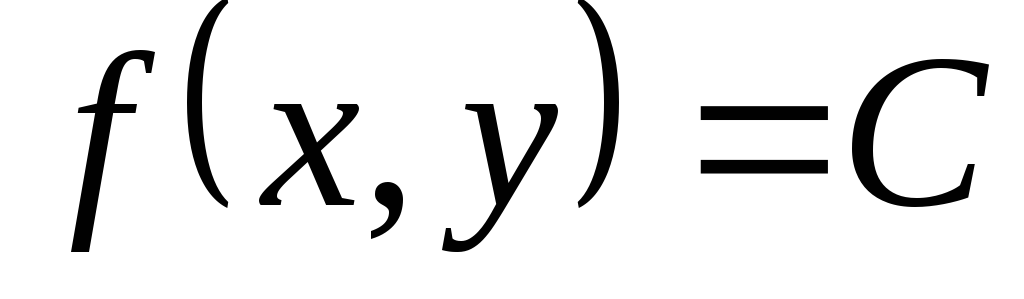 . .
Ответ:
1)
ЗАДАНИЕ
N 28
(-
выберите один вариант ответа)
(I.
стр.58)
Даны
функции спроса
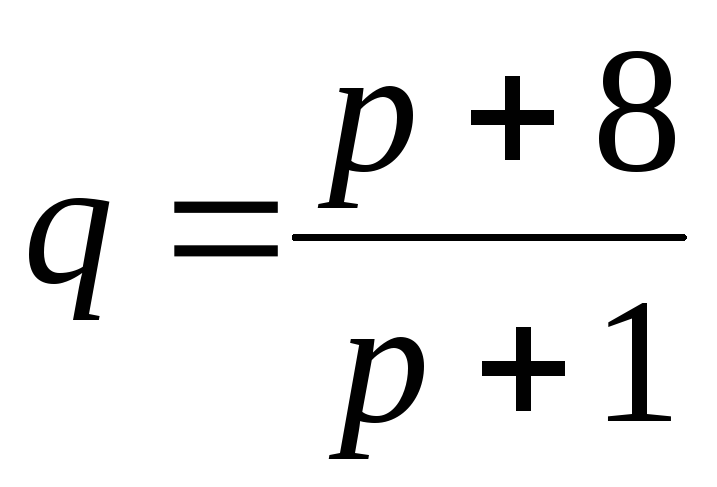 и
предложения и
предложения
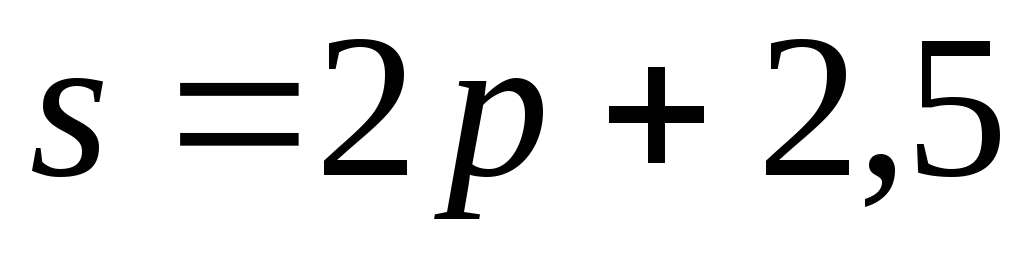 ,
где р
– цена товара. Тогда равновесная
цена
равна… ,
где р
– цена товара. Тогда равновесная
цена
равна…
Варианты
ответов:
1)
5,5;
2) 1;
3) 4,5;
4) 2,75.
Решение:
Равновесная цена определяется
уравнением
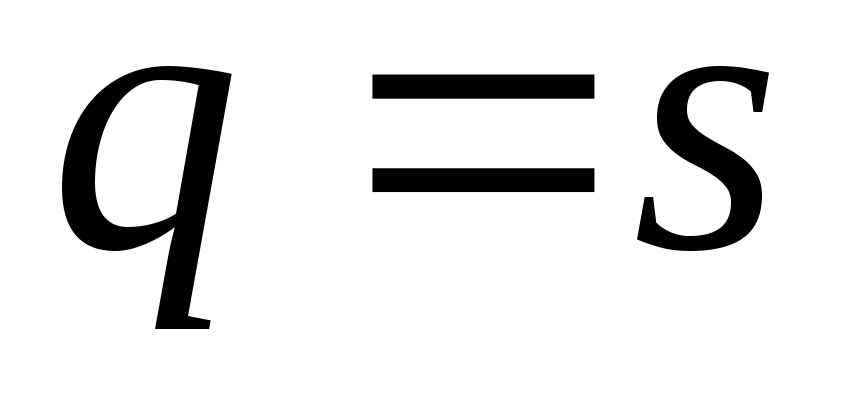 .
Для задачи получим .
Для задачи получим
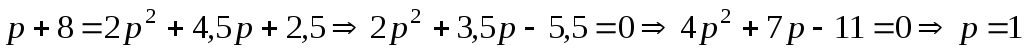 . .
Ответ:
2)
|


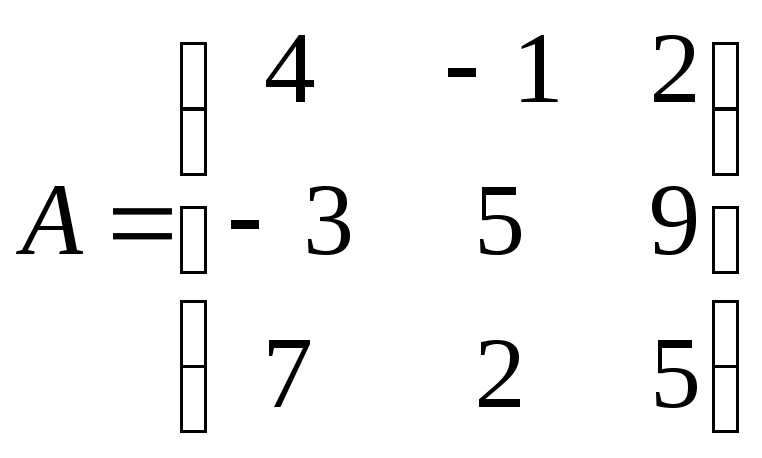 .
Тогда алгебраическое дополнение
элемента
.
Тогда алгебраическое дополнение
элемента
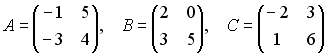 .
Установите
соответствие между двумя
множествами
.
Установите
соответствие между двумя
множествами базисными
(несвободными) переменными можно
считать…
базисными
(несвободными) переменными можно
считать… равен …
равен …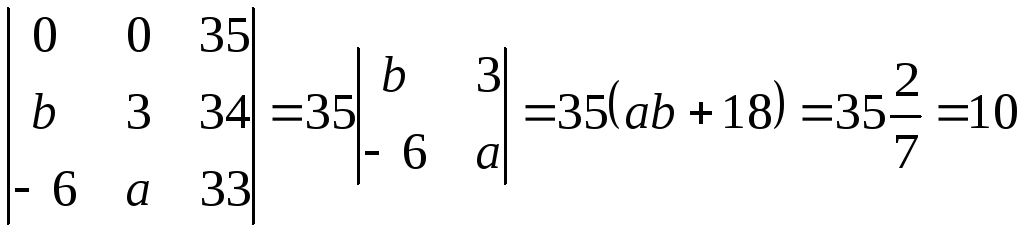 .
.









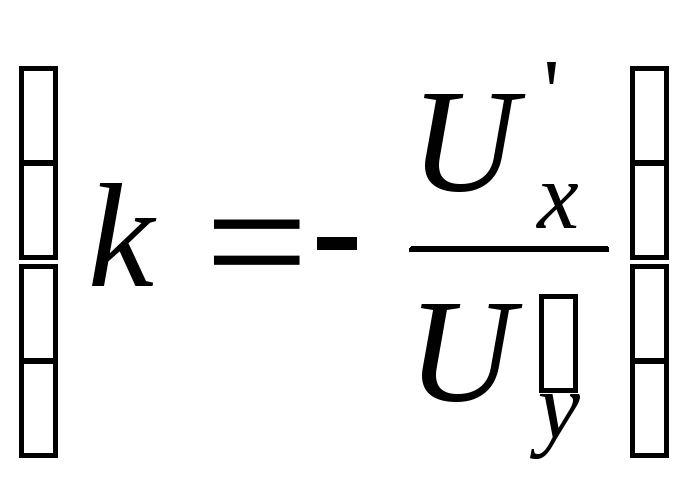 равна
…
равна
…