1.9. Поиск экстремума функции одной переменной.

При решении задач поиска максимума (минимума) выделяют локальный (с указанием границ) и глобальный максимум (минимум). Локальный минимум функции одной переменной ищет встроенная функция [x, y]=fminbnd(name, a, b, options). В ней:

• name имя М-функции,

• a, b границы поиска,

• options параметры управляющие ходом решения,

• x, y координаты точки минимума.

Для вычисления локального максимума, надо взять функцию name с другим знаком. Для примера, рассмотрим функцию y(x)=x⁴-0.5x³-28x²+140

Сначала найдем минимум на интервале, например, от -4 до -2.

[x,y]=fminbnd(@ext,-4,-2), где @ext обращение к М-функции вычисляющей интересующую нас функцию.

Потом найдем максимум на интервале от -6 до 6, для этого обратимся не к @ext, а к @ext_2, в которой функция y(x) взята с другим знаком, то есть y(x)=-(x⁴-0.5x³-28x²+140). То есть ее минимум будет максимумом исходной функции.

Получим и в том, и в другом случае координаты точки минимума (максимума) на заданном отрезке, что и требовалось.

1.10. Поиск экстремума функции нескольких переменной.

Минимум функции нескольких переменных z=f(x₁, x₂, …, x_n) осуществляет встроенная функция [X,Z]=fminsearch(name, x0, options) где:

• name имя М-функции вычисляющей z=f(x1, x2, …, xn),

• х0 вектор из n элементов, содержащих координаты точки начального приближения,

• options параметры управляющие ходом решения,

• Х вектор из n элементов, содержащий значения переменных, при которых функция z=f(x1, x2, …, xn) минимальна,

• Z это и есть минимальное значение функции.

Например, [X, Z]=fminsearch(@extr, [3 2]); где @extr обращение к М-функции extr, вычисляющей значение интересующей нас функции z=x₁²+x₂²-6x₂-2x₁+11, причем заданы начальные приближения [3 2] для х₁ и х₂ соответственно. В результате получим значения переменных в точке минимума и значение функции в минимуме.

Глава 2. Моделирование простых гидравлических систем

В MATLAB предусмотрена возможность создания полноценных графических приложений, содержащих различные элементы управления (кнопки, окна, полосы прокрутки и т. д.). Эти приложения можно вызывать из командной строки – нужно просто набрать имя, под которым приложение было сохранено.

Для создания подобных приложений служит среда GUIDE, которая вызывается из командного окна MATLAB командой guide. Следует заметить, что это требует определенных навыков.

Начинающему пользователю MATLAB лучше сперва ознакомиться со всем, что предлагается, по очереди. Файл с графическим интерфейсом имеет расширение .fig, а файл с текстом программы – расширение .m. Для того, чтобы увидеть текст программы находясь в графической среде GUIDE, надо запустить (командой Run или одноименной кнопкой с зеленым треугольником) и сохранить созданный графический интерфейс в файл с расширением fig. После этого откроется файл с тем же именем и расширением .m, который будет содержать текст программы.

2.1. Стационарный режим движения жидкости

К простым гидравлическим системам (рис.2.1.) относятся технологические схемы трубопроводов, для которых принимаются следующие допущения:

• во всех трубах протекает однофазный поток жидкости, температура которого одинакова на всех участках;

• все трубы располагаются на одном уровне, в системе нет рециклических (обратных) потоков, или рециклов, не учитываются местные сопротивления и перепады давлений в трубах, т. е. рассматриваются, так называемые короткие трубопроводы;

• системы включают только клапаны (вентили) с постоянными, не изменяющимися коэффициентами пропускной способности и закрытые емкости (аккумуляторы), давление газа в которых подчиняется идеальным законам.

Реальные гидравлические системы включают насосы, компрессоры и другие единицы оборудования; в них наряду с жидкостью могут перемещаться потоки газа, газо- и парожидкостной смеси. Тем не менее, изучение общих принципов построения математических моделей простых гидравлических систем позволяет получить представление о стратегии их математического моделирования.

Рис. 2.1. Простая гидравлическая система

Для системы, изображенной на рис. 2.1, будут справедливы два уравнения массового баланса (третье возможное балансовое уравнение – уравнение общего баланса – получается сложением двух других, т. е. будет линейно-зависимым):

; (1)

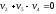. (2)

Формула для определения скорости протекания жидкости через клапан в соответствии с уравнением Бернулли для суммарной удельной энергии элементарной струи идеальной жидкости при установившемся движении и с учетом допущений о простой гидравлической системе имеет вид:

, (3)

где k – коэффициент пропускной способности клапана, Р_вх, Р_вых – давления жидкости на входе и на выходе из клапана.

Более строгая запись формулы (3) имеет вид:

, (4)

где sgn(x) – функция знака и может принимать только три значения: –1, 0, +1 в соответствии со схемой:

sgn(x) = – 1, если х < 0;

sgn(x) = 0, если х = 0; (5)

sgn(x) = +1, если х > 0.

При этом знак скорости потока жидкости становится отрицательным, если направление ее движения будет противоположным направлению, указанному на рис. 2.1.

Так как гидравлическая система содержит 5 клапанов, то приведенных формул (3) в системе уравнений математического описания должно быть 5.

По аналогии, должно быть две группы уравнений, определяющих давление жидкости внизу закрытой емкости и давление газа над поверхностью жидкости. При этом принимаются допущения:

• об идеальном поведении газа в емкости;

• о цилиндрической форме закрытой емкости с площадью поперечного сечения S и геометрической высотой Н^G;

• об одинаковом давлении газа Р_N в емкостях, не заполненных жидкостью.

В соответствии со следствием из закона Паскаля давление жидкости Р_жидк внизу емкости определяется по формуле:

Р_жидк. = P_газ + gH, (6)

где Р_газ – давление газа над поверхностью жидкости;  – плотность жидкости; Н – уровень жидкости в емкости.

Для определения давления газа Р_газ используется соотношение для идеального газа:

= =const, (7)

где 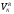– объем пустой емкости, т. е. не заполненной жидкостью,=S  H^G; – объем газа в закрытой емкости,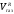=S (H^G – H).

В результате будет справедливо:

Р_газ S (H^G – H) = P_N S H^G

или

. (8)

Формулы для определения давления жидкости Р_жидк (6) и давления газа Р_газ (8) используются для описания поведения двух закрытых емкостей в гидравлической системе, изображенной на рис. 2.1.