3.2. Теплообменник типа смешение–вытеснение

Рис. 3.7. Схематическое изображение теплообменника смешение–вытеснение

Представленная схема змеевикового теплообменника включает в себя два потока теплоносителей – поток в резервуаре c начальной температурой (на входе в аппарат) , конечной температурой (на выходе), расходом, теплоёмкостьюи поток в змеевике c начальной температурой (на входе в аппарат), конечной температурой (на выходе), расходом, теплоёмкостью. Длина змеевика обозначена L.

Для построения математического описания данной модели примем следующие допущения:

• поток, проходящий через резервуар, описывается гидродинамической моделью идеального смешения;

• поток в змеевике описывается гидродинамической моделью идеального вытеснения;

• рассматривается стационарный режим работы теплообменника;

• коэффициент теплопередачи считается постоянным;

• кроме теплопередачи никаких процессов не происходит;

• теплоёмкости теплоносителей одинаковы и не меняются с изменением температуры.

Математическое описание процесса

Уравнение теплового баланса для потока теплоносителя в резервуаре для рассматриваемой гидродинамической модели идеального перемешивания в случае стационарного режима записывается как

1 . (32)

Выражение для локальной интенсивности теплопередачи для потока теплоносителя в резервуаре:

2 . (33)

Уравнение теплового баланса для потока в змеевике (гидродинамический режим идеального вытеснения) записывается следующим образом:

3 . (34)

Выражение для локальной интенсивности теплопередачи для потока теплоносителя в змеевике:

4 . (35)

С учётом равенства (27) выведем уравнение общего теплового баланса:

. (36)

В уравнении (36) произведение 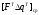представляет собой усреднённое по длине змеевика значение.

Уравнение теплового баланса для потока в змеевике (34) записывается через ∆q^T с учётом (27) следующим образом:

. (37)

Для того чтобы определить скорость теплопередачи в рассматриваемой модели теплообменника, необходимо найти площадь криволинейной трапеции под линией на рис. 3.8, то есть проинтегрировать функцию по длине змеевика и разделить на длину змеевика, в результате чего получается усредненное значение :

. (38)

Рис. 3.8. Зависимость функции от длины змеевика

При расчете (38) с учетом (37) будет справедливо:

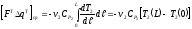. (39)

Подставляя выражение для функции (39) в (36), получаем уравнение общего теплового баланса для змеевикового теплообменника:

. (40)

Таким образом, система уравнений математического описания рассматриваемой модели теплообменника будет состоять из следующих уравнений:

уравнение общего теплового баланса:

1 ;

обыкновенное дифференциальное уравнение в явном виде для потока теплоносителя в змеевике:

2 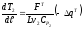; (41)

выражение для локальной скорости теплопередачи:

3 .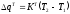

Кроме этого, для решения дифференциального уравнения 2 системы (41) (получение частного решения на компьютере) к данной системе уравнений математического описания необходимо добавить начальное условие:

2′ .

В качестве определяемых переменных для решения системы интегро-дифференциальных уравнений (41) необходимо выбрать зависимость температуры теплоносителя в змеевике от длины змеевика, температуру теплоносителя в резервуаре, локальную скорость теплопередачи и начальную температуру теплоносителя в змеевике:

. (42)

В данном случае дополнительное условие 2′ задаётся при одном значении независимой переменной, то есть решается задача Коши.

Решение дифференциального уравнения 2 системы (41) схематически показано на рис. 3.9.

Рис. 3.9. Зависимость температуры теплоносителя в змеевике от длины змеевика

Уравнение 2 системы (41) для решения на компьютере представляется в конечно-разностной форме согласно нумерации системы (41 – это будет уравнение :

, (43)

где – правая часть дифференциального уравнения (37) и конечно-разностного уравнения (43), расчет которой необходим для определения дискретных значений функции.

Уравнение 1 (корректирующее уравнение) – это внешний цикл решения задачи; уравнение 2 – цикл решения дифференциального уравнения, внутренний цикл решения задачи.

Корректирующее уравнение 1 представляется в следующем виде:

, (44)

где – функция этого уравнения, решаемого относительно.

Во внешнем цикле решения может быть применен, например, метод половинного деления для решения одного уравнения (44).

Во внутреннем цикле решается дифференциальное уравнение (37) или соответственно (43) (например, методом Эйлера) при каждом очередном приближении Т₁.