Глава 3. Моделирование стационарных режимов процессов теплопередачи в теплообменниках различных типов

Движение потоков теплоносителей в теплообменниках для целей компьютерного моделирования представляется идеальными гидродинамическими моделями, что позволяет получать адекватные компьютерные модели без излишнего усложнения математического описания.

Гидродинамические модели идеального смешения и идеального вытеснения для потоков теплоносителей можно применять для поверхностных теплообменников следующих типов:

• кожухотрубные теплообменники;

• трубчатые теплообменники;

• аппараты воздушного охлаждения;

• пластинчатые теплообменники;

• змеевиковые теплообменники.

Рис. 3.1. Кожухотрубный теплообменник

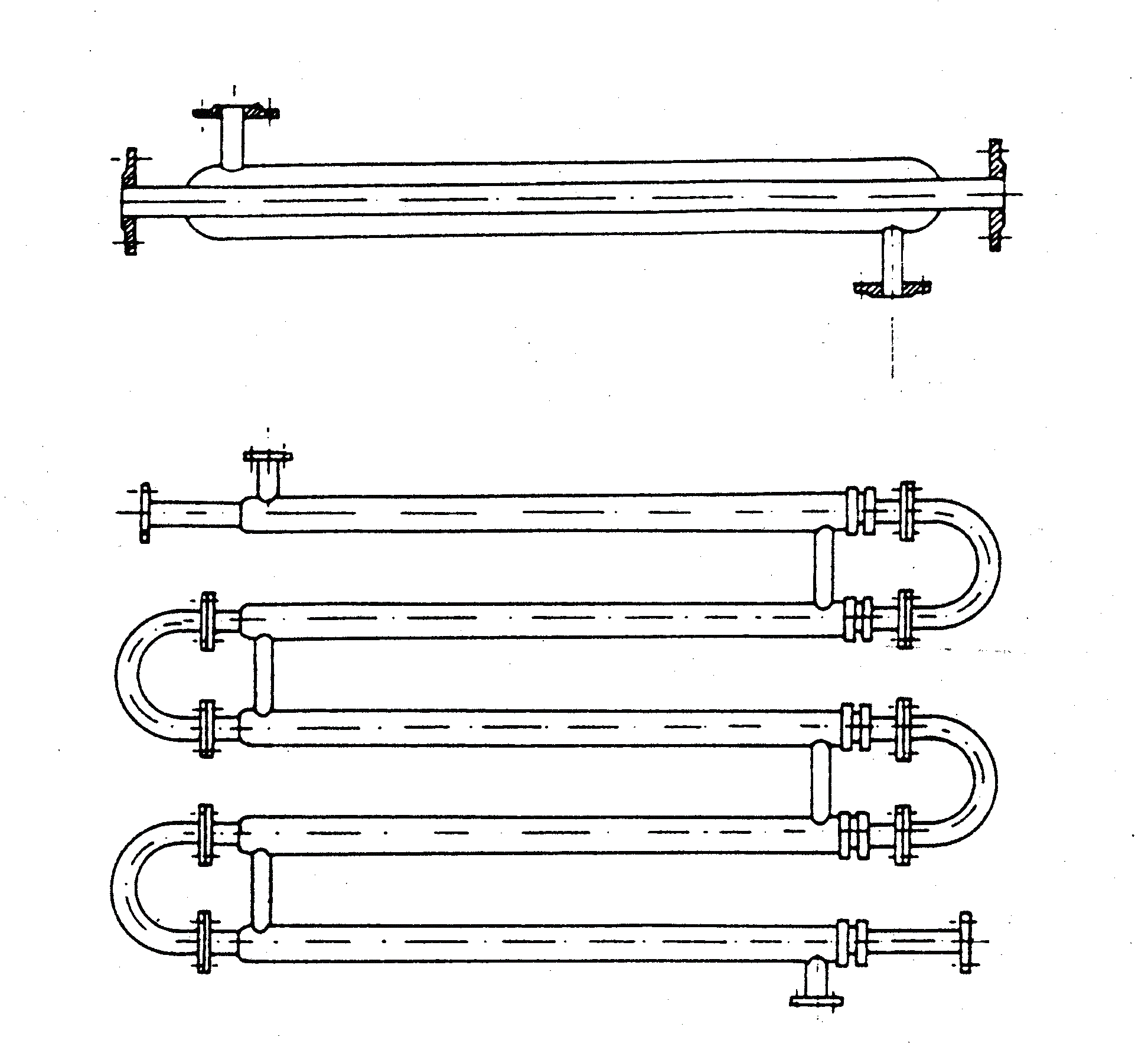
Рис. 3.2. Трубчатый теплообменник

Рис. 3.3. Змеевиковый теплообменник

В настоящем разделе приведены алгоритмы поверочно-оценочного расчётов стационарных режимов типовых фрагментов поверхностных теплообменников, в которых учитываются только процессы теплопередачи.

3.1. Теплообменник типа смешение–смешение

Рис. 3.4. Схематическое изображение теплообменника типа смешение–смешение

Представленная на рис. 3.4 схема теплообменника включает в себя два потока теплоносителей – например, охлаждаемый поток c начальной температурой (на входе в аппарат) , конечной температурой (на выходе), расходом, теплоёмкостьюи нагреваемый поток c начальной температурой (на входе в аппарат), конечной температурой (на выходе), расходом, теплоёмкостью. Поверхность теплообмена имеет площадь. Коэффициент теплопередачи обозначен.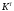

Для упрощения построения математического описания рассматриваемого процесса принимаются следующие допущения:

• стационарный режим теплопередачи;

• модель идеального смешения для обоих потоков теплоносителей;

• происходит только процесс теплопередачи.

Математическое описание процесса

В уравнение теплового баланса для потока первого теплоносителя рассматриваемой гидродинамической модели (идеального перемешивания) производная по времени равна нулю, так как рассматривается стационарный режим:

1 , (23)

где – локальнаяинтенсивность теплопередачи.

В систему уравнений математического описания необходимо включить выражение для локальной интенсивности теплопередачи для первого потока теплоносителя:

2 . (24)

Уравнение теплового баланса для потока второго теплоносителя (нижний индекс «2») имеет аналогичный (23) вид:

3 . (25)

Выражение для локальной интенсивности теплопередачи для второго потока теплоносителя также включается в систему уравнений математического описания:

4 . (26)

Учитывая, что локальные интенсивности теплопередачи обоих потоков совпадают по величине, но различны по знаку, можно записать:

(27)

Это даёт возможность сократить количество уравнений, входящих в систему линейных алгебраических уравнений математического описания для данной модели теплообменника.

В результате система уравнений математического описания стационарных режимов процесса в теплообменнике типа смешение–смешение записывается следующим образом:

1 ;

2 ; (28)

3 .

Рассмотрим следующий частный случай.

Принимается допущение о том, что константа теплопередачи через поверхность теплообмена постоянна (K^T = const). Это означает, что, в частности, теплоёмкости потоков и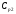постоянны и не зависят от температуры.

В этом случае система из трёх уравнений (28) позволяет найти три определяемых переменных. В качестве определяемых переменных выбираем температуры потоков на выходе из теплообменника Т₁ и Т₂, локальную интенсивность теплопередачи Δq^T.

Для решения системы (28) преобразуем ее путём подстановки в уравнения 1 и 2 выражения для локальной интенсивности теплопередачи Δq^T:

1 ; (29)

2 .

Обозначив коэффициенты перед переменными Т₁ и Т₂ как «a» с соответствующими индексами и свободный член уравнений 1 и 2 системы (29) как «b» также с соответствующими индексами, получаем возможность записать систему в матричном виде:

(30)

откуда методом обратной матрицы находим значения температур потоков на выходе из теплообменника Т₁, Т₂:

(31)

После определения температур потоков на выходе из теплообменника из уравнения 3 системы (28) определяется значение локальной интенсивности теплопередачи Δq^T. Таким образом определяются все три искомые переменные.