
RGR-3-po-LINEJNOJ-ALGEBRE
.pdf
Вариант 1
№1. Вычислить определитель матрицы
.
№2. Выполнить действия A(B–C)-1D, где
.
№3. Решить матричное уравнение
№4. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x1 2x2 3x3 x4 54x1 8x2 13x3 x4 19
x1 2x2 2x3 6x4 10
№5. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов
|
|
|
|
|
|
|
|
Вариант 2 |
|
|
|
|
|
||||||||
№1. Вычислить определитель матрицы |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№2. Выполнить действия A(B–C)-1D, где |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 2 |
3 |
8 |
5 |
3 |
5 |
3 |
|
1 |
4 |
3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A |
|
, B |
3 |
3 |
2 |
|
, C |
2 |
2 |
|
3 |
|
, D |
7 |
2 |
. |
|||||
1 1 |
8 |
|
7 |
1 7 |
|
|
3 |
|
|
3 |
2 |
|
|
1 |
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
№3. Решить матричное уравнение 





№4. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x1 2x2 3x3 x4 85x1 10x2 16x3 x4 39
x1 2x2 2x3 7x4 11
№5. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов

|
|
|
|
|
|
|
Вариант 3 |
|
|
|
|
|
||||||||||
№1. Вычислить определитель матрицы |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
№2. Выполнить действия A(B–C)-1D, где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 3 |
4 |
9 |
5 |
3 |
6 |
3 |
|
1 |
4 |
4 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A |
|
, B |
4 |
3 |
3 |
|
, C |
2 |
2 |
|
3 |
|
, D |
9 |
3 |
. |
||||||
1 0 |
10 |
|
7 |
1 7 |
|
|
3 |
|
3 |
2 |
|
|
2 |
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
№3. Решить матричное уравнение 





№4. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x1 2x2 3x3 x4 116x1 12x2 19x3 x4 65
x1 2x2 2x3 8x4 12
№5. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов
|
|
|
|
|
|
|
|
|
Вариант 4 |
|
|
|
|
|
||||||||
№1. Вычислить определитель матрицы |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№2. Выполнить действия A(B–C)-1D, где |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2 |
1 |
1 |
7 6 |
4 |
|
3 |
4 |
1 |
|
|
6 |
1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A |
5 |
|
, B |
1 |
3 |
1 |
, C |
|
2 |
2 |
4 |
|
, D |
|
2 |
1 . |
||||||
0 |
4 |
|
9 |
2 |
|
|
|
4 |
|
|
4 2 |
|
|
|
1 |
|
||||||
|
|
|
|
8 |
|
|
|
|
|
|
|
2 |
||||||||||
№3. Решить матричное уравнение 





№4. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x1 2x2 4x3 x4 33x1 6x2 13x3 x4 8
x1 2x2 3x3 5x4 14
№5. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов

|
|
|
|
|
|
|
|
Вариант 5 |
|
|
|
|
|
|
||||||||
№1. Вычислить определитель матрицы |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№2. Выполнить действия A(B–C)-1D, где |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 |
1 3 |
9 |
6 |
4 |
5 |
4 |
1 |
|
|
6 |
3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A |
|
, B |
3 3 |
1 |
|
, C |
2 |
2 |
4 |
|
, D |
|
6 |
1 |
. |
|||||||
0 |
3 8 |
|
9 |
2 |
8 |
|
|
4 |
|
|
4 2 |
|
|
|
1 |
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
№3. Решить матричное уравнение 





№4. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x1 2x2 4x3 x4 115x1 10x2 21x3 x4 54
x1 2x2 3x3 7x4 18
№5. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов
|
|
|
|
|
|
|
|
|
Вариант 6 |
|
|
|
|
|
|
|||||||||
№1. Вычислить определитель матрицы |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
№2. Выполнить действия A(B–C)-1D, где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
2 |
4 |
10 |
6 |
4 |
|
|
6 |
4 |
|
|
1 |
6 |
4 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
A |
|
|
, B |
4 |
3 |
2 |
|
, C |
|
|
2 2 |
4 |
|
, D |
8 |
2 |
. |
|||||||
0 |
2 10 |
|
9 |
2 |
8 |
|
|
|
|
4 |
|
4 |
2 |
|
|
2 |
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
№3. Решить матричное уравнение 





№4. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x1 2x2 4x3 x4 156x1 12x2 25x3 x4 89
x1 2x2 3x3 8x4 20
№5. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов

|
|
|
|
|
|
|
Вариант 7 |
|
|
|
|
|
|||||||||
№1. Вычислить определитель матрицы |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
№2. Выполнить действия A(B–C)-1D, где |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3 |
2 |
1 |
8 |
7 |
5 |
3 |
5 |
|
1 |
8 |
1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A |
7 |
|
, B 1 |
3 |
2 |
|
, C |
2 |
2 |
|
5 |
|
, D |
1 |
2 |
. |
|||||
1 |
4 |
|
|
9 |
|
|
5 |
|
5 |
2 |
|
|
1 |
3 |
|
||||||
|
|
|
11 3 |
|
|
|
|
|
|
||||||||||||
№3. Решить матричное уравнение 





№4. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x1 2x2 5x3 x4 43x1 6x2 16x3 x4 11
x1 2x2 4x3 5x4 19
№5. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов
|
|
|
|
|
|
Вариант 8 |
|
|
|
|
|
||||||||||
№1. Вычислить определитель матрицы |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№2. Выполнить действия A(B–C)-1D, где |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
3 |
1 |
2 |
9 |
7 |
5 |
4 |
5 |
|
1 |
8 |
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A |
6 |
|
, B 2 |
3 |
1 |
, C |
2 |
2 |
|
5 |
|
, D |
3 |
3 |
. |
||||||
1 |
6 |
|
|
|
|
5 |
|
5 |
2 |
|
|
0 |
1 |
|
|||||||
|
|
|
11 3 |
9 |
|
|
|
|
|
||||||||||||
№3. Решить матричное уравнение 





№4. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x1 2x2 5x3 x4 94x1 8x2 21x3 x4 35
x1 2x2 4x3 6x4 22
№5. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов

|
|
|
|
|
|
|
Вариант 9 |
|
|
|
|
|
|
|||||||||
№1. Вычислить определитель матрицы |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№2. Выполнить действия A(B–C)-1D, где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3 |
1 |
4 |
11 |
7 |
5 |
6 |
5 |
|
|
1 |
8 |
4 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
A |
|
|
, B 4 |
3 |
1 |
|
, C |
2 2 |
5 |
|
, D |
7 |
1 |
. |
||||||||
1 |
4 10 |
|
3 9 |
|
|
5 |
5 |
2 |
|
|
2 |
3 |
|
|||||||||
|
|
|
11 |
|
|
|
|
|
||||||||||||||
№3. Решить матричное уравнение 





№4. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x1 2x2 5x3 x4 19
6x1 12x2 31x3 x4 113
x1 2x2 4x3 8x4 28
№5. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов
|
|
|
|
|
|
|
Вариант 10 |
|
|
|
|
|
|||||||||
№1. Вычислить определитель матрицы |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
№2. Выполнить действия A(B–C)-1D, где |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4 |
3 |
1 |
9 |
8 |
6 |
3 |
6 |
|
1 |
|
10 |
1 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A |
9 |
|
, B 1 |
3 |
3 |
|
, C |
2 |
2 |
|
6 |
|
, D |
0 |
3 |
. |
|||||
2 |
4 |
|
4 |
10 |
|
|
6 |
|
6 2 |
|
|
1 |
4 |
|
|||||||
|
|
|
13 |
|
|
|
|
|
|
||||||||||||
№3. Решить матричное уравнение 





№4. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x1 2x2 6x3 x4 53x1 6x2 19x3 x4 14
x1 2x2 5x3 6x4 24
№5. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов

|
|
|
|
|
|
|
Вариант 11 |
|
|
|
|
|
||||||||
№1. Вычислить определитель матрицы |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
№2. Выполнить действия A(B–C)-1D, где |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4 |
2 |
2 |
10 8 |
6 |
4 |
6 |
|
1 |
10 |
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A |
8 |
|
, B 2 |
3 |
2 |
|
, C |
2 |
2 |
|
6 |
|
, D |
2 |
2 |
. |
||||
2 |
6 |
|
4 |
10 |
|
|
6 |
6 |
2 |
|
|
0 |
4 |
|
||||||
|
|
|
13 |
|
|
|
|
|
||||||||||||
№3. Решить матричное уравнение 





№4. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x1 2x2 6x3 x4 114x1 8x2 25x3 x4 43
x1 2x2 5x3 6x4 28
№5. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов
|
|
|
|
|
|
Вариант 12 |
|
|
|
|
||||||||||
№1. Вычислить определитель матрицы |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
№2. Выполнить действия A(B–C)-1D, где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4 |
1 |
3 |
11 |
8 |
6 |
5 |
6 |
|
1 |
10 |
3 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A |
7 |
|
, B 3 |
3 |
1 |
, C |
2 |
2 |
|
6 |
|
, D |
4 |
1 . |
||||||
2 |
8 |
|
|
|
|
6 |
|
6 |
2 |
|
|
1 |
|
|||||||
|
|
|
13 |
4 10 |
|
|
|
|
4 |
|||||||||||
№3. Решить матричное уравнение 





№4. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x1 2x2 6x3 x4 175x1 10x2 31x3 x4 84
x1 2x2 5x3 7x4 32
№5. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов

|
|
|
|
|
|
|
|
|
Вариант 13 |
|
|
|||||||||
№1. Вычислить определитель матрицы |
|
|
|
|
|
|
|
|
. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№2. Выполнить действия A(B–C)-1D, где |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
||||||||||||||
1 |
2 |
1 |
6 5 |
2 |
4 |
2 |
1 |
1 |
1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A |
|
|
, B |
1 |
3 |
2 |
|
, C |
3 2 |
2 |
|
, D |
6 |
2 . |
||||||
4 |
0 5 |
|
5 |
1 |
7 |
|
|
2 |
|
2 |
3 |
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
1 |
|||||||||||
№3. Решить матричное уравнение 





№4. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x1 3x2 2x3 x4 04x1 12x2 9x3 x4 1x1 3x2 x3 6x4 7
№5. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов
|
|
|
|
|
|
|
|
|
|
Вариант 14 |
|
|
|
|||||||||
№1. Вычислить определитель матрицы |
|
|
|
|
|
|
|
|
. |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№2. Выполнить действия A(B–C)-1D, где |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
1 |
3 |
2 |
7 |
5 |
2 |
|
5 |
2 |
1 |
1 |
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A |
1 |
|
, B |
2 3 |
3 |
|
, C |
|
3 2 |
2 |
|
, D |
8 |
3 |
. |
|||||||
4 |
7 |
|
5 |
1 |
7 |
|
|
|
2 |
|
2 |
3 |
|
|
1 |
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
№3. Решить матричное уравнение 





№4. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x1 3x2 2x3 x4 25x1 15x2 11x3 x4 9x1 3x2 x3 7x4 7
№5. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов

|
|
|
|
|
|
|
|
|
|
Вариант 15 |
|
|
|||||||||
№1. Вычислить определитель матрицы |
|
|
|
|
|
|
|
|
|
. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№2. Выполнить действия A(B–C)-1D, где |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
1 |
4 |
3 |
8 |
5 |
2 |
6 |
2 |
1 |
1 |
3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A |
2 |
|
, B |
3 3 |
4 |
|
, C |
3 2 |
2 |
|
, D |
10 |
4 . |
||||||||
4 |
9 |
|
5 |
1 |
7 |
|
|
2 |
|
|
2 |
3 |
|
|
0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
1 |
|||||||||||
№3. Решить матричное уравнение 





№4. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x1 3x2 2x3 x4 4
6x1 18x2 13x3 x4 23x1 3x2 x3 8x4 7
№5. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов
|
|
|
|
|
|
|
|
Вариант 16 |
|
|
|
|
|
||||||
№1. Вычислить определитель матрицы |
|
|
|
|
|
|
. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
№2. Выполнить действия A(B–C)-1D, где |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 2 |
1 |
6 |
7 |
4 |
|
|
2 |
4 |
1 |
|
5 |
1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A |
|
, B |
1 3 |
2 |
|
, C |
|
|
3 |
2 |
4 |
|
, D |
0 |
2 |
. |
|||
2 6 |
1 |
|
9 |
1 |
9 |
|
|
|
|
4 |
|
4 3 |
|
|
4 |
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
№3. Решить матричное уравнение 





№4. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x1 3x2 4x3 x4 62x1 6x2 9x3 x4 13
x1 3x2 3x3 4x4 17
№5. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов

|
|
|
|
|
|
|
Вариант 17 |
|
|
|
|
|
|||||||||
№1. Вычислить определитель матрицы |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№2. Выполнить действия A(B–C)-1D, где |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
1 1 2 |
9 |
7 |
4 |
5 |
4 |
|
1 |
5 |
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A |
|
, B |
2 |
3 |
1 |
|
, C |
3 |
2 |
|
4 |
|
, D |
6 |
1 |
. |
|||||
|
2 3 7 |
|
9 |
1 9 |
|
|
4 |
|
|
4 |
3 |
|
|
1 |
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
№3. Решить матричное уравнение 





№4. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x1 3x2 4x3 x4 65x1 15x2 21x3 x4 29
x1 3x2 3x3 7x4 23
№5. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов
|
|
|
|
|
|
|
Вариант 18 |
|
|
|
|
|
||||||||||
№1. Вычислить определитель матрицы |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
№2. Выполнить действия A(B–C)-1D, где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 2 |
3 |
10 |
7 |
4 |
6 |
4 |
|
1 |
5 |
3 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A |
|
, B |
3 |
3 |
2 |
|
, C |
3 |
2 |
|
4 |
|
, D |
8 |
2 |
. |
||||||
2 2 |
9 |
|
9 |
1 9 |
|
|
4 |
|
4 |
3 |
|
|
0 |
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
№3. Решить матричное уравнение 





№4. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x1 3x2 4x3 x4 106x1 18x2 25x3 x4 59
x1 3x2 3x3 8x4 25
№5. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов

|
|
|
|
|
|
|
Вариант 19 |
|
|
|
|
|
|
||||||
№1. Вычислить определитель матрицы |
|
|
|
|
|
|
|
|
. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
№2. Выполнить действия A(B–C)-1D, где |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 3 |
1 |
7 8 |
5 |
|
|
2 |
5 |
1 |
7 |
1 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A |
|
, B |
1 3 |
3 |
|
, C |
|
|
3 2 |
5 |
|
, D |
1 |
3 |
. |
||||
1 8 |
1 |
|
11 2 |
10 |
|
|
|
|
5 |
|
5 |
3 |
|
|
4 |
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
№3. Решить матричное уравнение 


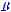


№4. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x1 3x2 5x3 x4 72x1 6x2 11x3 x4 15
x1 3x2 4x3 4x4 28
№5. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов
|
|
|
|
|
|
Вариант 20 |
|
|
|
|
|
||||||||||
№1. Вычислить определитель матрицы |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
№2. Выполнить действия A(B–C)-1D, где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
1 |
1 |
9 |
8 |
5 |
4 |
5 |
|
1 |
7 |
1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A |
6 |
|
, B 1 |
3 |
1 |
, C |
3 |
2 |
|
5 |
|
, D |
3 |
2 |
. |
||||||
1 |
5 |
|
|
|
|
5 |
|
5 |
3 |
|
|
2 |
2 |
|
|||||||
|
|
|
11 |
2 10 |
|
|
|
|
|
||||||||||||
№3. Решить матричное уравнение 





№4. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x1 3x2 5x3 x4 3
4x1 12x2 21x3 x4 11x1 3x2 4x3 6x4 28
№5. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов
