Сравнение нескольких дисперсий нормальных генеральных совокупностей

Пусть генеральные совокупности X₁ ,…, X_l распределены нормально. Из этих совокупностей извлечены независимые выборки объемов n₁ , n₂,…, n_l соответственно. По выборкам найдены исправленные выборочные дисперсии s,…, s. Требуется сравнить дисперсии генеральных совокупностей.

Схема сравнения D(X₁), …, D(X_l)

1. Выдвинуть нулевую гипотезу: D(X₁)=D(X₂)=…= D(X_l);

2. Задать число α – уровень значимости нулевой гипотезы;

3. Найти из табл. П 2.5 распределения χ² (см. приложение 2) значение χ²_крит по заданному α и числу степеней свободы l – 1 ;

4. Найти число ,

где ,

, ,;

5. Сравнить числа χ²_крит и B_набл :

• если B_набл > χ²_крит , то отвергнуть гипотезу H₀ ,

• если B_набл < χ²_крит то нет основания отвергать гипотезу H₀ .

Замечание 5. В случае принятия гипотезы H₀ в качестве оценки дисперсии генеральной совокупности за дисперсию этой генеральной совокупности принимают число 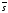².

Сравнение двух средних нормальных генеральных совокупностей

Пусть даны две независимые выборки объемов n₁ и n₂ соответственно из нормально распределенных генеральных совокупностей X и Y. По выборкам найдены оценки математических ожиданий ,и исправленные выборочные дисперсииs , s . Требуется сравнить M(X) и M(Y) генеральных совокупностей.

Схема сравнения M(X) и M(Y)

1. Выдвинуть нулевую гипотезу: H₀ : M(X) = M(Y) .

В качестве конкурирующей гипотезы рассмотреть

H₁ : M(X) ≠ M(Y) ;

2. Задать число α – уровень значимости нулевой гипотезы;

3. Найти по табл. П 2.6 распределения Стьюдента (см. приложение 2) значение T_крит по заданному α и числу k = n₁ + n₂ – 2;

4. Найти число ;

5. Сравнить числа T_крит и T_набл :

• если >T_крит , то отвергнуть гипотезу H₀ ,

• если <T_крит , то нет основания отвергать гипотезу H₀ .

Замечание 6. Если необходимо проверить гипотезу H₀: M(X) = M(Y) о равенстве средних двух нормальных генеральных совокупностей X и Y при условии известных дисперсий σи σ, то в описанной выше схеме вместоT_крит используют число N_крит , определяемое с помощью табл. П 2.2 (см. приложение 2) по заданному α из равенства:

Вместо T_набл по данным выборок вычисляют число

.

Если <N_крит, то нет основания отвергать гипотезу H₀ .

Если >N_крит, то гипотезу H₀ отвергают.

Задачи с решениями

Задача 9.1. По двум независимым выборкам объемов n₁ = 10 и n₂ = 15, извлеченным из нормальных генеральных совокупностей X и Y, найдены оценки дисперсий: s = 8,42, s = 4,23. При уровне значимости α = 0,05 проверить гипотезу H₀: D(X)=D(Y) при конкурирующей гипотезе H₁: D(X)>D(Y).

Решение. 1) По данным выборки вычисляем

=.

2) По табл. П 2.7 (см. приложение 2), учитывая значения

α = 0,05, k₁ = n₁ – 1 = 9 , k₂ = n₂ – 1 = 14.

находим число: F_крит = 2,65.

3) Сравниваем: так как 1,99 < 2,65, т.е. F_набл < F_крит , то нет основания отвергать гипотезу H_0.

Ответ: гипотеза H₀ : D(X)=D(Y) принимается.

Задача 9.2. По двум независимым выборкам объемов n₁=10 и n₂=15, извлеченным из нормальных генеральных совокупностей X и Y, найдены оценки дисперсий: S= 8,42, S= 4,23. При уровне значимости α = 0,1 проверить гипотезу H₀: D(X)=D(Y) при конкурирующей гипотезе H₁: D(X)≠D(Y).

Решение. 1) По данным выборки вычисляем

=.

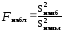2) По табл. П 2.7 (см. приложение 1), учитывая значения

α = 0,1 и ,k₁ = n₁ – 1 = 9 , k₂ = n₂ – 1 = 14.

находим число: F_крит = 2,65.

3) Сравниваем: так как 1,99 < 2,65, т.е. F_набл < F _крит , то нет основания отвергать гипотезу H_0.

Ответ: гипотеза H₀ : D(X)=D(Y) принимается.

Задача 9.3. По трем независимым выборкам объемов n₁ = 10 и n₂ = 15 и n₃ = 20, извлеченным из нормальных генеральных совокупностей X, Y и Z найдены оценки дисперсий: S= 3,62, S=4,23, S=7,45. При уровне значимости α = 0,05 проверить гипотезу H₀ : D(X)=D(Y)=D(Z).

Решение. 1) По данным выборок вычисляем:

k₁ = n₁ – 1=9, k₂ = n₂ – 1=14, k₃ = n₃ – 1=19.

= 9 + 14 + 19 = 42,

=

=

=.

=,

.

2) По табл. П 2.5 (см. приложение 2), учитывая значения

α = 0,05, k = 3 – 1 = 2,

находим число

χ²_крит = 6,0

3) Сравниваем: так как 2,06 < 6,0 , т.е. B_набл < χ²_крит , следовательно нет основания отвергать нулевую гипотезу.

Ответ: гипотезу H₀ : D(X) = D(Y) =D(Z) принимают.

Задача 9.4. По двум независимым выборкам объемов n₁=10 и n₂=16, извлеченным из нормальных генеральных совокупностей X и Y, найдены оценки математических ожиданий =2,5,=3,1 и исправленные выборочные дисперсииs =0,62, s=0,43 . Проверить нулевую гипотезу: H₀ : M(X) = M(Y) при конкурирующей гипотезе H₁ : M(X) ≠ M(Y) и уровне значимости α = 0,01.

Решение. 1) Так как s ≠ s, то предварительно проверим гипотезу H₀: D(X)=D(Y) о равенстве генеральных дисперсий при конкурирующей гипотезе H₁: D(X)>D(Y). Для этого поступаем по аналогии с решением 1 задачи.

а) По данным выборки вычисляем

=;

б) По табл. П 2.7 (см. приложение 2), учитывая значения

α = 0,01, k₁ = n₁ – 1 = 9 , k₂ = n₂ – 1 = 15.

находим число:

F_крит = 3,89.

в) Сравниваем: так как 1,44 < 3,89, т.е. F_набл < F_крит , то гипотеза о равенстве генеральных дисперсий принимается, то есть различие между s = 0,62 и s = 0,43 считаем незначительным.

2) Проверим гипотезу H₀ : M(X) = M(Y) о равенстве средних при конкурирующей гипотезе

H₁ : M(X) ≠ M(Y) .

а) Найдем по табл. П 2.6 (см. приложение 2) значение T_крит по заданному α = 0,01 и числу k = 10 + 16 – 2 = 24 :

T_крит = 2,8 .

б) Найдем число T_набл :

=

==

= .

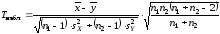в) Сравнить числа T_крит и : так как 2,101 < 2,8 то< T_крит и гипотеза H₀ : M(X) = M(Y) о равенстве средних принимается.

Ответ: гипотеза H₀ : M(X) = M(Y) принимается.

Задача 9.5. По двум независимым выборкам объемов n₁=10 и n₂=16, извлеченным из нормальных генеральных совокупностей X и Y, с дисперсиями σ=9, σ=12, вычислены оценки математических ожиданий=12,7,=10,2. При уровне значимости α = 0,05 проверить гипотезуH₀ : M(X) = M(Y) и конкурирующей гипотезе H₁ : M(X) ≠ M(Y).

Решение. Воспользуемся замечанием 6. 1) Вычислим:

= = 2,19.

2) Находим N_крит из уравнения

, то есть = 0,475

используя табл. П 2.2 (см. приложение 2).

Следовательно,

N_крит =1,96.

3) Сравниваем: так как 2,19 > 1,96, т.е. N_набл > N_крит , то гипотезу H₀ отвергают. Значит, различие генеральных математических ожиданий значительное.

Ответ: гипотеза H₀ : M(X) = M(Y) отвергается, т.е. M(X) ≠ M(Y).

Задачи

9.1. По двум независимым выборкам объемов n₁=10 и n₂=13, извлеченным из нормальных генеральных совокупностей X и Y , найдены исправленные выборочные дисперсии s=0,52 и s=0,28. При уровне значимости α = 0,01 проверить гипотезу H₀: D(X) = D(Y) при конкурирующей гипотезе H₁: D(X) > D(Y).

9.2. По двум независимым выборкам объемов n₁=15 и n₂=10, извлеченным из нормальных генеральных совокупностей X и Y , найдены исправленные выборочные дисперсии s=1,92 и s=3,21. При уровне значимости α = 0,1 проверить гипотезу H₀ : D(X)=D(Y) при конкурирующей гипотезе H₁: D(X) ≠ D(Y).

9.3. По двум независимым выборкам объемов n₁=15 и n₂=10, извлеченным из нормальных генеральных совокупностей X и Y c дисперсиями D(X)=25, D(Y)=32, найдены выборочные средние =53,= 61. При уровне значимости α = 0,1 проверить нулевую гипотезуH₀ : M(X)=M(Y) при конкурирующей гипотезе H₁ : M(X) ≠ M(Y).

9.4. По двум независимым выборкам объемов n₁=15 и n₂=12, извлеченным из нормальных генеральных совокупностей X и Y найдены выборочные средние =11,2,=15,7 и исправленные выборочные дисперсииs=0,58 , s=0, 83. При уровне значимости α = 0,05 проверить нулевую гипотезу H₀ : M(X)=M(Y) при конкурирующей гипотезе H₁: M(X) ≠ M(Y).

9.5. По трем независимым выборкам объемов n₁=10, n₂=12 и n₃=17, извлеченным из нормальных генеральных совокупностей X, Y и Z, найдены выборочные дисперсии D_в(X)=2,3, D_в(Y)=2,7 , D_в(Z)=4,5 При уровне значимости α = 0,05 проверить гипотезу H₀ : D(X) = D(Y) = D(Z).

9.6. По двум независимым выборкам объемов n₁=12 и n₂=18, извлеченным из нормальных генеральных совокупностей X и Y найдены исправленные выборочные дисперсии s=25,31 , s=10,23. При уровне значимости α = 0,05 проверить гипотезу H₀: D(X) = D(Y) при конкурирующей гипотезе H₁ : D(X) > D(Y).

9.7. По двум независимым выборкам объемов n₁=12 и n₂=10, извлеченным из нормальных генеральных совокупностей X и Y найдены исправленные выборочные дисперсии D_в(X)=12,3, D_в(Y)=18,5. При уровне значимости α = 0,02 проверить гипотезу H₀: D(X) = D(Y) при конкурирующей гипотезе H₁ : D(X) ≠ D(Y).

9.8. По двум независимым выборкам объемов n₁=40 и n₂=30, извлеченным из нормальных генеральных совокупностей X и Y c дисперсиями D(X) = 80, D(Y) = 70, найдены выборочные средние = 120, = 115. При уровне значимости α = 0,01 проверить нулевую гипотезу H₀ : M(X) = M(Y) при конкурирующей гипотезе H₁: M(X) ≠ M(Y).

9.9. Из двух партий изделий, изготовленных на двух одинаково настроенных станках, извлечены две выборки:

xi	2,2	2,6	2,8	3,1
mi	2	3	5	2

yi	2,5	2,7	2,8	3,0
mi	2	4	6	3

Проверить нулевую гипотезу H₀ : M(X)=M(Y) при конкурирующей гипотезе H₁ : M(X)≠M(Y) при уровне значимости α = 0, 1.

9.10. По четырем независимым выборкам объемов n₁=12 и n₂=15, n₃=18 и n₄=20 извлеченным из нормальных генеральных совокупностей X, Y, Z и U, найдены исправленные выборочные дисперсии S=0,27 , S=0,52, S=0,85 и S=0,99. При уровне значимости α = 0,01 проверить гипотезу H₀: D(X) =D(Y) = D(Z) = D(U).

Ответы

9.1. H₀ принимается: F_набл = 1,86 , F_крит = 4,39.

9.2. H₀ принимается: F_набл = 1,67 , F_крит = 2,65.

9.3. H₀ отвергается: N_набл =  5,36 , N_крит = 1,64.

9.4. H₀ отвергается: T_набл = 13,99 , T_крит = 2,06.

Указание. Предварительно проверить равенство дисперсий при заданном уровне значимости

9.5. H₀ принимается: B_набл = 4,064 , χ² _крит = 6,0.

9.6. H₀ отвергается: F_набл = 2,47 , F_крит = 2,41.

9.7. H₀ принимается: F_набл = 1,53 , F_крит = 4,63.

9.8. H₀ принимается: N_набл = 2,40 , N_крит = 2,58.

9.9. H₀ принимается: T_набл = 0,73 , T_крит = 1,71.

Указание: Предварительно проверить равенство дисперсий при заданном уровне значимости

9.10. H₀ принимается: B_набл. =2,918 , χ²=11,3.