
- •Оглавление
- •Задачи с решениями
- •§2. Случайные события и их классификация. Алгебра событий. Вероятность события. Теоремы сложения и умножения вероятностей Случайные события
- •Вероятность события
- •Теоремы сложения и умножения вероятностей
- •Задачи с решениями
- •§3. Формула полной вероятности. Повторные испытания. Формула Бернулли Формула полной вероятности
- •Повторные испытания. Формула Бернулли
- •Формулы Лапласа
- •Формула Пуассона
- •Задачи с решениями
- •Глава 2. Случайные величины §4. Дискретная случайная величина Понятие случайной величины. Закон распределения дискретной случайной величины
- •Фунция распределения
- •Свойства функции распределения
- •Числовые характеристики дискретной случайной величины
- •Свойства математического ожидания
- •Свойства дисперсии
- •Некоторые законы распределения дискретной случайной величины
- •§5. Непрерывная случайная величина Понятие непрерывной случайной величины. Функция распределения непрерывной случайной величины
- •Свойства функции распределения
- •Функция плотности распределения вероятностей
- •Свойства функции плотности распределения вероятностей
- •Числовые характеристики непрерывной случайной величины
- •§6. Некоторые законы распределения непрерывной случайной величины Равномерный закон распределения
- •Показательный (экспоненциальный) закон распределения
- •Нормальный закон распределения
- •"Правило трех сигм"
- •Глава 3. Элементы математической статистики §7. Статистическое распределение выборки Задачи математической статистики
- •Генеральная и выборочная совокупности
- •Статистическое распределение выборки. Полигон и гистограмма
- •Свойства функции (х)
- •Задачи с решениями
- •§8. Статистические оценки параметров Точечные статистические оценки параметров распределения
- •Интервальные оценки параметров нормального распределения
- •Задачи с решениями
- •§9. Проверка статистических гипотез Статистические гипотезы
- •Проверка гипотез
- •Сравнение двух дисперсий нормальных генеральных совокупностей
- •Сравнение нескольких дисперсий нормальных генеральных совокупностей
- •Сравнение двух средних нормальных генеральных совокупностей
- •Задачи с решениями
- •§10. Критерий согласия Пирсона Проверка гипотезы о нормальном распределении
- •Задачи с решениями
- •§11. Элементы теории корреляции
- •Коэффициент корреляции
- •Свойства коэффициента корреляции
- •Проверка значимости выборочного коэффициента корреляции
- •Линейная корреляция. Уравнение регрессии
- •Ранговая корреляция
- •Правило проверки наличия связи между качественными признаками
- •Приложение 1 Контрольные работы и контрольные вопросы по теории
- •Элементы теории вероятностей
- •Элементы математической статистики
- •3. Контрольные вопросы по теории
- •Приложение 2 Вероятностные таблицы
- •Значения функции
- •Критические точки распределения
- •Критические точки распределения Стьюдента
- •Критические точки распределения f Фишера – Снедекора
Оглавление
Глава 1. Вероятность случайного события 5
§ 1. Элементы комбинаторики 5
Основные понятия комбинаторики 5
Задачи с решениями 7
Задачи 9
Ответы 11
§2. Случайные события и их классификация. Алгебра событий. Вероятность события. Теоремы сложения и умножения вероятностей 11
Случайные события 11
Вероятность события 12
Теоремы сложения и умножения вероятностей 13
Задачи с решениями 14
Задачи 19
Ответы 22
§3. Формула полной вероятности. Повторные испытания. Формула Бернулли 23
Формула полной вероятности 23
Повторные испытания. Формула Бернулли 24
Формулы Лапласа 24
Формула Пуассона 25
Задачи с решениями 25
Задачи 30
Ответы 33
Глава 2. Случайные величины 33
§4. Дискретная случайная величина 33
Понятие случайной величины. Закон распределения дискретной случайной величины 33
Фунция распределения 35
Некоторые законы распределения дискретной случайной величины 39
Задачи 41
Ответы 44
§5. Непрерывная случайная величина 46
Понятие непрерывной случайной величины. Функция распределения непрерывной случайной величины 46
Функция плотности распределения вероятностей 47
Числовые характеристики непрерывной случайной величины 50
Задачи 51
Ответы 54
§6. Некоторые законы распределения непрерывной случайной величины 55
Равномерный закон распределения 55
Показательный (экспоненциальный) закон распределения 57
Нормальный закон распределения 58
Задачи 60
Ответы 63
Глава 3. Элементы математической статистики 64
§7. Статистическое распределение выборки 64
Задачи математической статистики 64
Генеральная и выборочная совокупности 64
Статистическое распределение выборки. Полигон и гистограмма 65
Задачи с решениями 66
Задачи 70
Ответы 72
§8. Статистические оценки параметров 78
Точечные статистические оценки параметров распределения 78
Интервальные оценки параметров нормального распределения 80
Задачи с решениями 82
Задачи 87
Ответы 90
§9. Проверка статистических гипотез 90
Статистические гипотезы 90
Проверка гипотез 91
Сравнение двух дисперсий нормальных генеральных совокупностей 92
Сравнение нескольких дисперсий нормальных генеральных совокупностей 93
Сравнение двух средних нормальных генеральных совокупностей 94
Задачи с решениями 95
Задачи 100
Ответы 101
§10. Критерий согласия Пирсона 102
Проверка гипотезы о нормальном распределении 102
Задачи с решениями 104
Задачи 109
Ответы 111
§11. Элементы теории корреляции 111
Коэффициент корреляции 112
Линейная корреляция. Уравнение регрессии 115
Ранговая корреляция 117
Задачи 125
Ответы 128
Приложение 1 128
Контрольные работы и контрольные вопросы по теории 128
1.Элементы теории вероятностей 128
2.Элементы математической статистики 134
3. Контрольные вопросы по теории 142
Приложение 2 144
Вероятностные таблицы 144
Глава 1. Вероятность случайного события
§ 1. Элементы комбинаторики
Основные понятия комбинаторики
Комбинаторикой (комбинаторным анализом) называют раздел математики, в котором изучаются задачи выбора и расположения элементов из некоторого основного (обычно конечного) множества в соответствии с заданными правилами.
Многие комбинаторные задачи могут быть решены с помощью следующих двух важных правил, называемых правилами суммы и произведения.
Правило суммы. Если объект А может быть выбран из некоторой совокупности объектов m способами, а другой объект В – n способами, то выбрать либо А, либо В можно m+n способами.
Правило произведения. Если объект А может быть выбран из некоторой совокупности объектов m способами и после каждого такого выбора объект В может быть выбран n способами, то пара объектов А и В в указанном порядке может быть выбрана m · n способами.
Эти правила распространяются на случай трёх и большего числа объектов.
Кроме этих правил известны формулы, помогающие решать некоторые типовые задачи, встречающиеся довольно часто. Комбинациям, фигурирующим в этих задачах, присвоены особые названия – размещения, перестановки и сочетания.
Определение 1. Размещениями из n элементов по m (m ≤ n) элементов в каждом называются комбинации, содержащие по m различных элементов, выбранных из данных n элементов, которые отличаются либо составом, либо порядком входящих в них элементов.
Число
всех возможных размещений из n
элементов
по m
обозначается символом
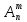 и вычисляется по формуле:
и вычисляется по формуле:
 =
n ∙ (
n – 1)
∙ … ∙ (
n
– m + 1)=
=
n ∙ (
n – 1)
∙ … ∙ (
n
– m + 1)=
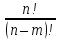 .
.
Определение 2. Перестановками из n различных элементов называются комбинации, состоящие из одних и тех же n элементов и отличающиеся только порядком расположения элементов.
Число
всех возможных перестановок из n
элементов обозначается символом
 и вычисляется по формуле:
и вычисляется по формуле:
 =
n
∙ (
n
1)
∙ … ∙2
∙1=
n !
=
n
∙ (
n
1)
∙ … ∙2
∙1=
n !
Нетрудно заметить, что перестановки из n элементов являются частным случаем размещений из n элементов по m, когда m = n, т.е. число элементов в комбинации совпадает с числом имеющихся элементов. Таким образом, справедлива формула:
 =
= .
.
Определение 3. Сочетаниями из n элементов по m (m ≤ n) в каждом называются комбинации, содержащие по m различных элементов, выбранных из данных n элементов, которые отличаются составом входящих в них элементов. При этом порядок расположения элементов не играет роли.
Число
всех возможных сочетаний из n
элементов по m
обозначается
символом
 и вычисляется по формуле:
и вычисляется по формуле:
 =
=
 =
=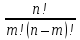 ,т.
е.
,т.
е.
 =
=
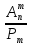 .
.
Свойства сочетаний:
 =
1,
=
1,
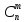 =
=
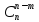 ,
,
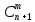 =
=
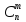 +
+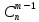 ,
,
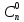 +
+
 +
+ + … +
+ … + =
= .
.
Определение 4. Размещениями с повторениями из n элементов по m элементов в каждом называются комбинации, содержащие по m возможно повторяющихся элементов, выбранных из данных n элементов, которые отличаются либо составом, либо порядком входящих в них элементов.
Число
всех возможных размещений с повторениями
из n
элементов по m
обозначается символом
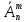 и вычисляется по формуле:
и вычисляется по формуле:
 =
=
 .
.
