Методы уточнения корней уравнений с одним неизвестным.

Метод деления отрезка пополам (дихотомии). Пусть функция, заданная выражением (5.5) на отрезке [Т_min , T_max], где Т_min < T_max , является непрерывной и имеет единственный корень, поскольку f(Т_min)< 0,а f(T_max) >0, (здесь Т_min и T_max - температуры кипения самого легкого и самого тяжелого компонента соответственно). f(T)

Для уточнения корня методом

деления отрезка пополам поступим

следующим образом (см. рис. 1). Раз-

делим отрезок [Т_min,T_max] пополам и

вычислим значение функции f(Т) в Т_min Т_cp T_max

средней точке. Если значение f(Т_cp)= 0,

то T_cp является решением уравнения, T

если f(Т_cp) 0, то в качестве следующе-

го отрезка, на котором расположен ко-

рень, будет выбран тот, на концах ко-

торого, функция имеет противополож-

ные знаки. В данном случае при f(Т_cp)<0 в Рисунок 1.

дальнейшем рассматривается отрезок [Т_cp,T_max], при f(Т_cp)>0 - отрезок [Т_cp,T_max]. Повторяя аналогичные действия с одним из выбранных отрезков, получим некоторую последовательность вложенных отрезков, предельная точка которых есть решение уравнения. Очевидно, что условием окончания будет ситуация, когда либо значение функции близко к нулю с заданной степенью точности, либо длина отрезка не превосходит заданной величины .

Метод секущих. f(T)

При использовании метода секущих

для уточнения корня уравнения (5.5)деление T₂ T₃ T₁

отрезка определения функции производитсяТ

в отношении, пропорциональном значениям

функции в конечных точках. В этом случае

график функции последовательно заменя- Рисунок 2.

ется прямой линией, проходящей через две точки, расположенные на кривой. Предположим, что известны значения функции при Т₁ и Т₂, т.е. имеются две точки [T₁,f(T₁)] и [T₂,f(T₂)].

Следующее приближение определяется как значение Т, соответствующее точке пересечения прямой, проходящей через [T₁,f(T₁)] и [T₂,f(T₂)]. Для этого запишем уравнение прямой,проходящей через две точки, задав f(Т₃) =0 (см. рис.2):

или (5.6)

Отсюда, к+1 - ое приближение будет вычисляться по формуле:

(5.7)

Условием окончания вычислительного процесса можно считать выполнение условия: .

Метод касательных (метод Ньютона). Пусть функция f(Т)=0 на отрезке [Т_min , T_max] дифференцируема, и первая и вторая производные ее не меняют знака. Исходя из некоторого начального приближения Т₁ вычислим значение Т₂ , используя разложение функции в окрестности Т₁ в ряд Тейлора до второго члена включительно, то есть запишем уравнение касательной к функции f(Т₁ ) в точке Т₁ (см. рис. 3).

f(Т₂)-f(Т₁) = f ’(Т₁)( Т₂ - Т₁) (5.8) f(Т)

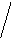
Тогда, полагаяf(Т₂) = 0, найдем точку пересечения касательной с осью абцисс: T₂ =T₁ - f(T₁)/f‘(T₁) (5.9)

Последующие значения Т будут определяться по формуле:

T_k+1=T_k - f(T_k)/f’(T_k) (5.10) T_k+1 T_k T

Рисунок 3

Условием окончания вычислительного процесса является:

.

Метод простой итерации.

Представим уравнение (5.5) в виде T=(T) (5.11)

где (T) - некоторая функция Т, для которой выполняется условие: ,Тогда для решения уравнения (5.11) можно будет воспользоваться методом простой итерации, который заключается в следующем.

Представим уравнение уравнение (5.11) в виде системы двух уравнений:

 y = Т

 y = (Т) (5.12)

Тогда, очевидно, решением уравнения (5.12) будет абцисса точки пересечения графиков этих функций (рис. 4).

f(T)

Задаваясь некоторым начальным приближением Т₀ по уравнению (5.11) вычислим Т₁ = (Т₀). Если , то используяT₁ в качестве нового приближения, вычислим по уравнению (5.11) Т₂. Этот процесс продолжается до тех пор, пока на некотором шагеk+1 не будет

выполнено условие . T₂ T₁ T₀ T

Важно отметить, что последовательность Рисунок 4.

Т₀ ,Т₁, ...T_k+1, будет сходящейся (к существующему

корню) если для (Т) на отрезке [Т_min,T_max] выполняется условие в каждой вычисляемой точке.

Комбинированный метод - метод секущих и касательных.

При использовании данного методаf(T)

щих для уточнения корня уравнения (5.5) наf(T_b)

интервале [T_a,T_b] на каждой i-й итерации Т_1k

имеем два приближения T_ik и T_ic между T_a T_1c T_b

которыми находится точное значение корня,

которое может быть найдено в на последую-

щих итерациях. f(T_a) T