1.5. Характеристика состояния электрона в атоме системой квантовых чисел

Уравнение Шредингера (1.16) часто записывают в компактной форме:

, (1.17)

где – гамильтониан, оператор энергии.

Оператор – это математический аппарат, воздействующий на Ψ-функцию с целью получения собственного значения. Например, гамильтониан – оператор полной энергии, воздействуя на Ψ-функцию, позволяет получить собственное значение полной энергии системы.

Отметим еще раз, что Ψ-функция – однозначная, конечная и непрерывная функция, имеющая нулевое значение в тех областях пространства, где нет частицы.

Решение уравнения Шредингера для атома водорода возможно лишь в полярной системе координат, где вместо декартовых координат x,y,zиспользуются радиус-вектор и два угла (рис. 1.4).

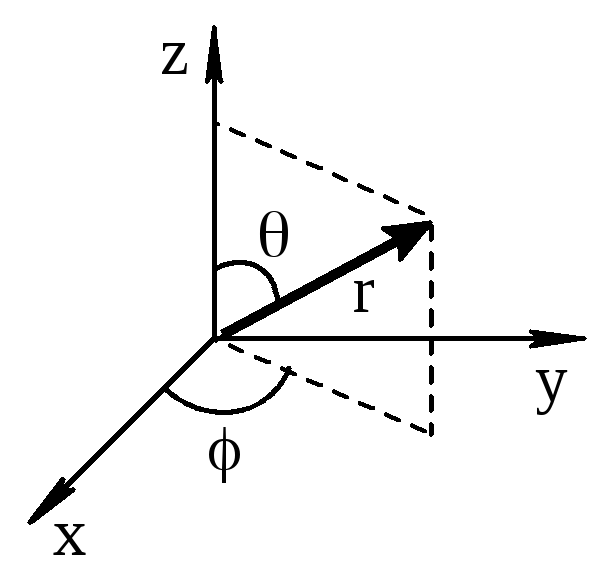
Рис. 1.4. Полярная система координат

Это решение приводит к неожиданному результату. Волновая функция электрона зависит не только от трёх координат (r, θ, φ), но и от трёх целочисленных параметров, названных квантовыми числами. Их традиционное обозначениеn(как квантовое число в теории Бора), ℓ иm_ℓ.

В результате решения уравнения Шредингера в полярной системе координат находят волновую функцию в виде произведения:

(1.18)

; ;

Выражение R(r)называется радиальной функцией распределения (радиальной составляющей волновой функции), а произведение– угловой составляющей.

Главное квантовое число nв значительной степени определяет значение энергии электрона в атоме и размеры электронного облака. Оно принимает положительные целочисленные значения от 1 до бесконечности. С ростомnвозрастают размеры электронного облака и энергия электронов. Вспомните, в теории Бора энергия электрона пропорциональна!

Кроме цифрового обозначения nиспользуется и буквенная индексация:

n = 1, 2, 3, 4 …

K, L, M, N …

Совокупность электронов, характеризующихся одним и тем же значением главного квантового числа, называют электронным слоем(школьное название – электронный уровень). Соответственно говорят о первом илиK-слое, втором илиL-слое, третьем илиM-слое и т.д.

Второе квантовое число (ℓ), называемое орбитальным (побочным, в иностранной литературе – азимутальным) квантовым числом, характеризует энергию электрона внутри слоя (уровня) и определяет форму электронного облака. Оно принимает положительные целочисленные значения, начиная с нуля, но имеет ограничение: при данном значении главного квантового числа nвеличина ℓ не может превысить значение (n–1). На практике побочное квантовое число чаще обозначается буквами:

ℓ = 0, 1, 2, 3, 4,…, n–1

s, p, d, f, g,…

Совокупность электронов c одним и тем же значением побочного квантового числа называют электронной оболочкой (подуровнем).Соответственно говорят обs-,p-,d-,f- и т. д. оболочках.

Третье квантовое число (m_ℓ), называемое магнитным, определяет ориентацию орбитали в пространстве. Орбиталь же образуется совокупностью электронов с одним и тем же значением магнитного квантового числа, её традиционно обозначают клеточкойٱ (квантовая ячейка). При данном значении ℓ, магнитное квантовое число принимает значения:

1, 2, 3, 4, …, ℓ

m_ℓ= 0

–1, –2, –3, –4, …, –ℓ

Общее число значений составляет (2ℓ+1).

Названные три квантовых числа непосредственно вытекают из решения уравнения Шредингера в трёхмерном мире. У электрона есть и четвертая квантовая характеристика – спиновое квантовое число m_s, отражающее четвёртую координату нашего мира – время. Спиновое квантовое число принимает (в единицах атомного мира) лишь два значения: +½ и –½. Договоримся считать значение +½ больше значения –½ и будем обозначать электроны со спином +½ стрелочкой, а электроны со спином –½ – стрелочкой.

Четыре квантовых числа есть полная и однозначная характеристика состояния электрона в атоме. Более того, в атоме не может быть двух электронов с одинаковым набором четырёх квантовых чисел(принцип Паули). Это – основной закон мира электронов. Принцип Паули позволяет рассчитать максимальное число электронов в слое, оболочке и на орбитали.

Орбиталь характеризуется постоянным значениемm_ℓ. Это возможно лишь при известном значении ℓ, что в свою очередь требует постоянства значенияn. Таким образом, для орбитали изменяется только спиновое квантовое число, отсюда следует, что на орбитали может быть максимально два электрона и они в соответствии с принципом Паули обязательно должны иметь противоположные спины:.

Возникает вопрос, а если на орбитали находится один электрон, то каково его состояние:или? Эта проблема регулируетсяправилом Хунда: суммарный спин электронов оболочки должен быть максимальным. Таким образом, в рамках принятых договорённостей единственный электрон на орбитали имеет спиновое квантовое число +½.

Оболочка характеризуется постоянным значением орбитального квантового числа, что возможно при известном значении главного квантового числа. Следовательно, для оболочки происходит изменение магнитного и спинового квантового чисел. При значении орбитального квантового числа равном ℓ число разрешённых значений магнитного квантового числа, а значит и число орбиталей в этой оболочке составляет (2ℓ+1) штук (ℓ положительных, ℓ отрицательных и ноль). Отсюда получаем, что максимальное число электронов в оболочке составит 2(2ℓ+1) или конкретно: для s-оболочки 2; дляp-оболочки 6; дляd-оболочки 10; дляf-оболочки 14 и т.д.

Наконец, для нахождения максимального числа электронов, могущих быть в данном слое, необходимо суммировать электроны всех оболочек этого слоя. Для слоя с главным квантовым числом nэто будут оболочки с ℓ =0, 1, 2, 3, …,n–1. Следовательно, ёмкость слоя составит:

Методом математической индукции легко показать, что эта сумма равна 2n². Отсюда максимальное число электронов составит: в первом слое (К-слое) 2; во втором слое (L-слое) 8; в третьем слое (М-слое) 18 и т.д.

Энергия электрона в атоме водорода (теория Бора) определяется единственным (главным) квантовым числом, а в многоэлектронном атоме – главным и орбитальным квантовыми числами. В целом энергия электрона возрастает по мере роста суммы названных квантовых чисел при доминирующем значении главного квантового числа. При одинаковой сумме энергия состояния с меньшим значением главного квантового числа ниже. В соответствии с этими правилами энергетический ряд атомных орбиталей выглядит следующим образом:

1s < 2s < 2p < 3s< 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s <

< 4f < 5d < 6p < 7s < 5f < 6d < 7p …

Для изображения атомных орбиталей используют значения волновой функции или её квадрата (точнее угловой части этой функции). Поскольку электронная орбиталь в принципе распространяется до бесконечности, то изображают её часть (например, 80 или 90%). На рис. 1.5 представлены формы 1s-, 2p- и 3d-орбиталей.

1s-орбиталь сферически симметрична, знак соответствующей функции одинаков в разных частях системы координат. Три 2p-орбитали представляют собой объёмные гантелеобразные фигуры, прошитые соответствующими осями координат. Четыре из пяти 3d-орбиталей представляют собой двугантельные образования, различно ориентированные в пространстве. Знаки соответствующих функций для гантелей различны. Пятая 3d-орбиталь представляет собой массивную гантель, насаженную на осьz, и тороидальную катушку в плоскостиxy.

Узловой поверхностью орбитали называют геометрическое место точек, где Ψ=0 (Ψ²=0). Узловые поверхности могут быть сферическими, плоскими и коническими. По определению каждая орбиталь имеет сферическую узловую поверхность с бесконечным радиусом.

Главное квантовое число равно общему числу узловых поверхностей данной орбитали. Например, любая из 3d-орбиталей имеет одну сферическую узловую поверхность и две плоские (две конические – для).

Побочное квантовое число равно числу узловых поверхностей орбитали, проходящих через начало координат. Например, любая из пяти

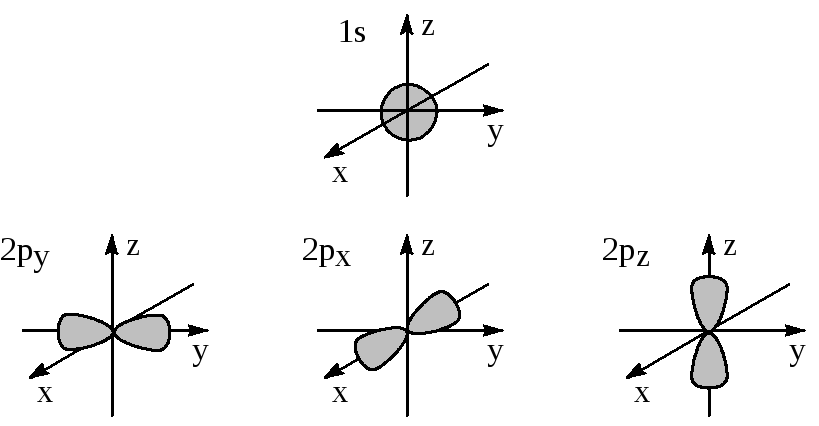
Рис. 1.5. Формы 1s, 2pи 3d-орбиталей

3d-орбиталей (ℓ=2) имеет по две узловые поверхности, проходящие через начало координат.

Отметим, что формы ns-орбиталей отличаются от формы 1s-орбитали, аналогичноnp-орбитали отличны от 2р-орбиталей. Однако при качественном рассмотрении вопросов химической связи, связанных с перекрыванием орбиталей, в определённом приближении можно считать любуюs-орбиталь сферически симметричной, а любую р-орбиталь – гантелеподобной.