Продолжение таблицы 2.3

1	2	3	4
Cl5+	88	I–	206
Cl7+	41	Ce3+	115
Cr6+	58	Nd3+	112
		Lu3+	100

Периодический закон ведёт к следующим закономерностям в изменении атомных и ионных радиусов.

1) В периодах слева направо в целом радиус атома уменьшается, хотя и неравномерно, затем в конце резко возрастает у атома благородного газа.

2) В подгруппах сверху вниз происходит рост радиуса атома: более значительный в главных подгруппах и менее значительный – в побочных. Эти закономерности легко объяснить с позиции электронного строения атома. В периоде при переходе от предыдущего элемента к последующему электроны идут в один и тот же слой и даже в одну и ту же оболочку. Рас-тущий заряд ядра ведёт к более сильному притяжению электронов к ядру, не компенсируемому взаимным отталкиванием электронов. В подгруппах увеличение числа электронных слоёв и экранирование притяжения к ядру внешних электронов глубинными слоями ведёт к росту радиуса атома.

3) Радиус катиона меньше радиуса атома и уменьшается с ростом заряда катиона, например:

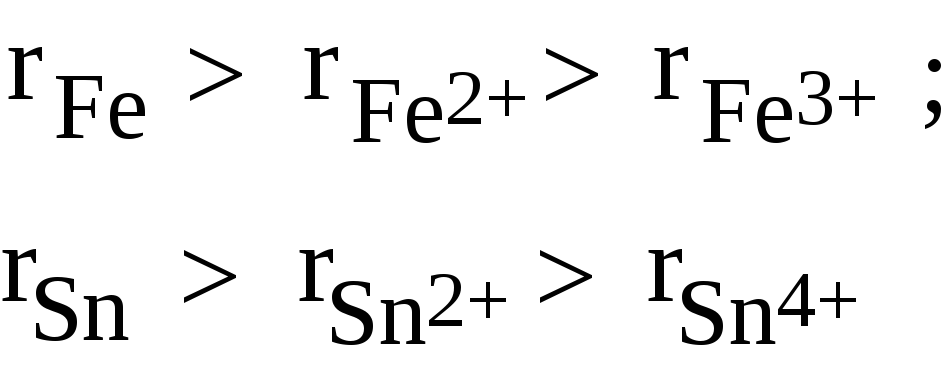
4) Радиус аниона больше радиуса атома, например:

5) В периодах радиусы ионов d-элементов одинакового заряда плавно уменьшаются, это так называемоеd-сжатие, например:

6) Аналогичное явление отмечается и для ионов f-элементов – в периодах радиусы ионовf-элементов одинакового заряда плавно уменьшаются, это так называемоеf-сжатие, например:

7) Радиусы однотипных ионов (имеющих сходную электронную “макушку”) в подгруппах плавно возрастают, например:

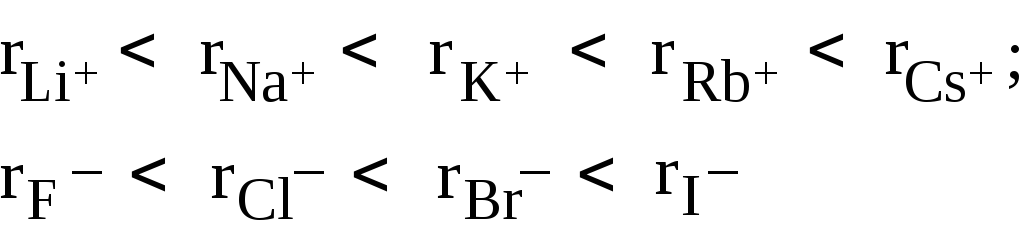
8) Если различные ионы имеют одинаковое число электронов (они называются изоэлектронными), то размер таких ионов, естественно, будет определяться зарядом ядра иона. Наименьшим будет ион с бóльшим зарядом ядра. Например, ионы Cl^–,S^2–,K⁺,Cа²⁺имеют одинаковое число электронов (18), это изоэлектронные ионы. Наименьшим из них будет ион кальция, поскольку у него наибольший заряд ядра (+20), а наибольшим – ионS^2–, у которого наименьший заряд ядра (+16). Таким образом, вырисовывается следующая закономерность: радиус изоэлектронных ионов уменьшается с ростом заряда иона.

Относительная сила кислот и оснований (схема Косселя)

Все кислородные кислоты и основания содержат в составе своих молекул фрагмент Эⁿ⁺ – О^2– – Н⁺. Хорошо известно, что диссоциация соединения по кислотному или основному типу связана со степенью окисления (более строго, с валентностью) атома элемента. Примем, что связь в этом фрагменте чисто ионная. Это достаточно грубое приближение, поскольку с ростом валентности атома полярность его связей значительно ослабевает (см. гл. 3).

В этом жёстком фрагменте, вырезанном из молекулы кислородной кислоты или основания, место разрыва связи и диссоциация соответственно с выбросом протона или гидроксил-аниона будут определяться величиной взаимодействия между ионами Эⁿ⁺и О^2–. Чем сильнее это взаимодействие, а оно будет возрастать с увеличением заряда иона (степень окисления) и уменьшением его радиуса, тем более вероятны разрыв связи О–Н и диссоциация по кислотному типу. Таким образом,сила кислородных кислот будет возрастать с увеличением степени окисления атома элемента и уменьшением радиуса его иона.

Отметим, что здесь и далее более сильным из двух является тот электролит, который при одинаковой молярной концентрации в растворе имеет бóльшую степень диcсоциации. Подчеркнём, что в схеме Косселя анализируются два фактора – степень окисления (заряд иона) и радиус иона.

Например, необходимо выяснить, какая из двух кислот более сильная – селеновая H₂SeO₄или селенистаяH₂SeO₃. ВH₂SeO₄ степень окисления атома селена (+6) выше, чем в селенистой кислоте (+4). Одновременно радиус ионаSе⁶⁺меньше радиуса ионаSе⁴⁺. В результате оба фактора показывают, что селеновая кислота сильнее селенистой.

Еще один пример, марганцевая кислота (HMnO₄) и рениевая (HReO₄). Степени окисления атомовMnиReв этих соединениях одинаковы (+7), поэтому следует сопоставить радиусы ионовMn⁷⁺иRe⁷⁺. Поскольку радиусы однотипных ионов в подгруппе возрастают, делаем вывод, что радиус ионаMn⁷⁺меньше, а значит марганцевая кислота сильнее.

Ситуация с основаниями будет противоположной. Сила оснований возрастает с падением степени окисления атома элемента и увеличением радиуса его иона. Отсюда, если один и тот же элемент образует различные основания, например, ЭОН и Э(ОН)₃, то второе из них будет слабее первого, поскольку степень окисления в первом случае меньше, а радиус иона Э⁺больше радиуса иона Э³⁺. В подгруппах сила однотипных оснований будет возрастать. Например, самым сильным основанием из гидроксидов щелочных металлов будетFrOH, а самым слабым –LiOH. Еще раз подчеркнём, что речь идёт о сравнении степеней диссоциации соответствующих электролитов и не касается вопроса об абсолютной силе электролита.

Используем этот же подход при рассмотрении относительной силы бескислородных кислот. Фрагмент Э^n– – Н⁺, имеющийся в молекулах этих соединений, заменяем ионной связью:

Сила взаимодействия между этими ионами, разумеется, определяется зарядом иона (степенью окисления атома элемента) и его радиусом. Имея в виду закон Кулона, получаем, что сила бескислородных кислот возрастает с уменьшением степени окисления атома элемента и увеличением радиуса его иона.

Сила бескислородных кислот в растворе будет возрастать в подгруппе, например, галогеноводородных кислот, поскольку при одинаковой степени окисления атома элемента увеличивается радиус его иона.