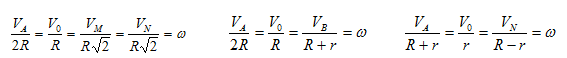термех12-20

     Плоскопараллельным (плоским) движением (ППД) твердого тела называется такое движение, при котором все точки тела перемещаются в плоскостях параллельных некоторой неподвижной плоскости (рисунок 2.11). 

    При таком движении точки, лежащие в разных плоскостях на одном отрезке, перпендикулярном неподвижной плоскости (например M₁M₂ ) совершают одинаковые движения.

Рисунок 2.11

Рисунок 2.12

    Отрезок M₁M₂  движется поступательно. Поэтому изучение плоскопараллельного движения сводится к изучению движения плоской фигуры в какой-то плоскости.

    На рисунке 2.12 показано перемещение пластинки в плоской системе отсчета xOy  из одного положения в другое. Такое перемещение можно осуществить двигая пластину поступательно с траекторией точки A  с последующим поворотом на угол φ  вокруг точки A₁. Это же перемещение можно выполнить иначе. 

    Например, перемещая пластинку поступательно с траекторией точки B , с последующим поворотом вокруг B₁  на угол φ. Траектории точек A  и B различны, а угол поворота в обоих случаях  одинаков. 

     Положение пластинки вполне определяется положением скрепленного с ней отрезка (например AB), закон движения которого можно задать в виде:

                                 x_A=x_A(t),  y_A=y_A(t),  φ=φ(t).

    Точка A  в этом случае называется полюсом. Если принять за полюс точку B , то получим уравнения:

                                x_B=xB(t),  y_B=yB(t),  φ=φ(t)

    За полюс выбирается точка, закон движения которой известен.

14. Мгновенный центр скоростей

16. Вращение твердого тела

17. Скорости и ускорения точек при вращении

Скорости и ускорения точек при вращении тела вокруг неподвижной точки

Скорости точек твердого тела, совершающего сферическое движение, в каждый момент времени определяются как их вращательные скорости при вращении вокруг мгновенной оси Ω (рисунок 3.4). Зная положение мгновенной оси вращения Ω и угловую скорость тела ω, можно определить скорость любой точки тела M как скорость этой точки во вращательном движении вокруг мгновенной оси по известной формуле

ν = ω × r ,

где r - радиус-вектор точки M, проведенный из неподвижной точки O.

Рис. 3.4

Модуль скорости

ν = ωr sin γ = ωhΩ,

где hΩ - расстояние точки от мгновенной оси вращения.

Введем подвижную Oxyz и неподвижную Ox1y1z1 системы координат аналогично рисунку 3.1.

Для проекций скорости точки на неподвижные и подвижные оси получены формулы Эйлера:

для неподвижной системы координат

для подвижной системы координат

Из формул (4), (5) можно получить уравнения мгновенной оси в неподвижной и подвижной системах координат, положив для точек, лежащих на мгновенной оси, все проекции скорости равными нулю.

Для неподвижной системы координат:

Для подвижной системы координат:

Если положение мгновенной оси Ω уже установлено, то для нахождения угловой скорости ω достаточно знать скорость ν какой-либо точки M, не лежащей на мгновенной оси (рисунок 3.4). Тогда, опустив из этой точки перпендикуляр hΩ на мгновенную ось Ω, получим ν = ω⋅ hΩ , откуда

ω = ν / hΩ.

Рис. 3.5

Для определения ускорения точки твердого тела служит теорема Ривальса: ускорение любой точки твердого тела при сферическом движении определяется как геометрическая сумма ее вращательного и осестремительного ускорений

a = aEвр + aΩос (3.8)

где aEвр = ε × r- вращательное ускорение точки,

aΩос = ω × ν- осестремительное ускорение точки.

Модули этих ускорений (рисунок 3.5)

aEвр = hEε и aΩос = hΩω2 (3.9)

где hE - расстояние от точки до оси углового ускорения E,

hΩ - расстояние от точки до мгновенной оси Ω.

Модуль ускорения точки можно найти как диагональ параллелограмма:

При сферическом движении осестремительное ускорение aΩос направлено по перпендикуляру, опущенному из точки на мгновенную ось Ω, а вращательное ускорение aEвр оказывается перпендикулярно плоскости проходящей через вектор углового ускорения ε и радиус-вектор r. Направление вращательного ускорения не совпадает с направлением скорости ν.

20.произвольное движение твердого тела .

19.2. Произвольное движение твердого тела и системы тел. Следствия из законов динамики Ньютона

 Октябрь 15th, 2011 |  fizportal.ru

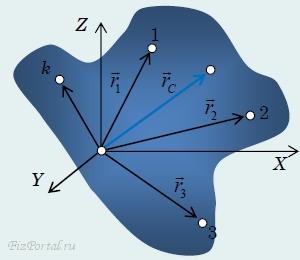
19.2. Произвольное движение твердого тела и системы тел

 Рассмотрим теперь уравнение второго закона Ньютона для произвольной системы материальных точек и их произвольного движения. Оказывается, что в этом случае можно рассматривать движение некоторой геометрической точки, для которой уравнение движения полностью определяется только внешними силами. В качестве такой точки следует взять центр масс системы.  Пусть совокупность тел представлена набором материальных точек, массы которых обозначим m₁, m₂, m₃..., положения этих точек определим с помощью их радиус-векторов r₁, r₂, r₃ ... в некоторой системе координат XYZ (рис. 103).

рис. 103

 Радиус-вектор центра масс системы определяется по формуле

 Аналогично можно выразить векторы скорости и ускорения центра масс системы через соответствующие характеристики движения материальных точек:

 В знаменателях этих формул стоит суммарная масса всей системы

m₁ + m₂ + m₃ + ... = m.

В числителе формулы (3) стоит то же выражение, что и в уравнении (3) §17. Поэтому из этих соотношений следует простое уравнение для ускорения центра масс: для произвольной системы независимо от того, движутся ли части этой системы друг относительно друга или нет, ускорение центра масс системы определяется уравнением a_c = F/m, в котором F − сумма внешних сил, действующих на систему, m− масса всей системы.  Мы определили особую точку системы материальных точек − центр масс. Фактически введение этого понятия оправдывается простотой уравнения, описывающего ее движение. Упрощенно можно сказать, что всю массу системы можно собрать в центре масс и при этом рассматривать движение системы как движение одной материальной точки. Существенно, что движение центра масс полностью определяется внешними силами и не зависит от внутренних сил, действующих между отдельными телами, входящими в рассматриваемую систему. Например, центр масс осколков разорвавшегося в воздухе снаряда продолжает двигаться по параболе (если, конечно, пренебречь сопротивлением воздуха) независимо от того, какие дополнительные скорости приобрели эти осколки в момент разрыва.  Отметим еще одно существенное обстоятельство: если в какой-либо инерциальной системе отсчета центр масс системы покоится, то никакие внутренние силы не могут изменить его положение. Для твердого тела, расстояния между точками которого остаются неизменными, центр масс однозначно «привязан» к самому телу.  Рассмотрим простейший пример твердого тела, состоящего из двух небольших шариков (материальных точек), массы которых равны m₁ и m₂, соединенных жестким невесомым стержнем длиной l (рис. 104).

рис. 104

 Направим ось вдоль стержня, начало отсчета совместим с первым шариком. Из определения (1), следует, что центр масс находится на стержне (координаты у, z обоих шариков равны нулю, поэтому и соответствующие координаты центра масс также равны нулю). Координата х_C центра масс рассчитывается по формуле (с учетом х₁ = 0, х₂ = l)

 Если массы шариков равны, то центр масс находится в середине стержня, если масса одного из шариков значительно превышает массу другого, то центр масс совпадает с массивным шариком. Так, при m₁ >> m₂, х_C = 0, в противном случае при m₁ << m₂, х_с = l. При произвольном соотношении между массами шариков центр масс находится ближе к более тяжелому шарику. Отметим интересное соотношение, следующее из формулы (4):

где l₁, l₂ − расстояния от центра масс до соответствующих материальных точек.  Для тел простой геометрической формы их центр масс может быть легко найден без громоздких вычислений по формуле (1). Так, для однородного стержня центр масс находится в его середине, для однородных кольца, диска, шара их центр масс совпадает с геометрическим центром. Центр масс однородной прямоугольной пластинки расположен в точке пересечения диагоналей, для треугольной пластинки − в точке пересечения медиан (рис. 105).

рис. 105

(Докажите эти утверждения самостоятельно.)