Поток отказов

2.4. Понятие о процессе восстановления (закономерности третьего вида)

Р

Рисунок 5.1 Формирование потока отказов от n изделий

анее были рассмотрены два вида закономерностей: изменение параметров технического состояния автомобилей по времени или пробегу и вариация параметров технического состояния. Эти закономерности достаточно точно характеризуют надежность автомобилей и их элементов, т. е. позволяют оценить среднюю наработку на отказ, вероятность отказа автомобиля при определенном пробеге, ресурсы его агрегатов и др.

Для рациональной организации производства необходимо, кроме того, знать, сколько отказов данного вида будет поступать в зоны ремонта в течение смены, недели, месяца; будет ли их количество постоянным, или переменным и от каких факторов оно зависит, т. е. речь идет не только о надежности конкретного автомобиля, но и группы автомобилей, например, автомобилей данной модели, колонны, АТП. При отсутствии этих сведений нельзя рационально организовать производство, т. е. определить необходимое число рабочих, размеры производственных площадей, расход запасных частей и материалов. Взаимосвязи между показателями надежности автомобилей и суммарным потоком отказов для группы автомобилей изучают с помощью закономерностей третьего вида, которые характеризуют процесс восстановления — возникновения и устранения отказов и неисправностей изделий во времени. Предположим, что фиксируются моменты появления однородных отказов в группе из п автомобилей (рис. 2.6). Очевидно, что наработки на отказы, во-первых, случайны для агрегата каждого автомобиля и описываются соответствующими функциями F(x) и f(x), во-вторых, независимы у одинаковых агрегатов разных автомобилей, в-третьих, при устранении отказа в зоне ремонта безразлично, от какого автомобиля поступает отказ и какой он по счету. К важнейшим характеристикам закономерностей третьего вида относятся: средняя наработка до k-го отказа

где — средняя наработка до первого отказа; — средняя наработка между первым и вторым отказом; — вторым и третьим и т. д.

События x₁, x₂, … x_k называются процессом восстановления.

Средняя наработка между отказами для п - автомобилей.

Между первым и вторым отказами . между (k—1)-ым и k -ым

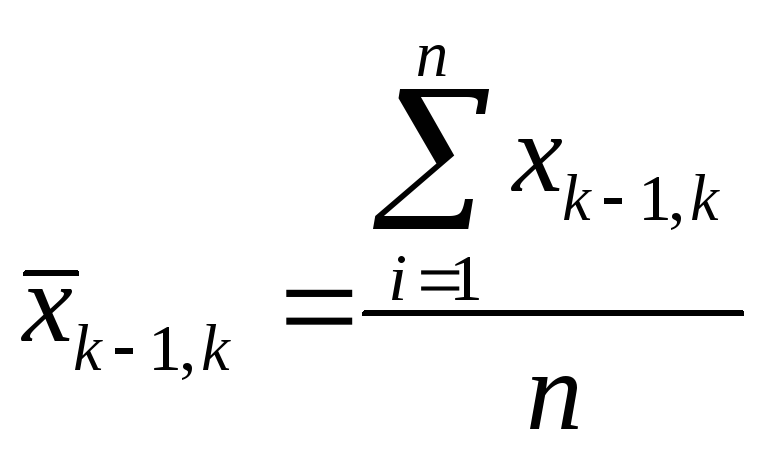
Коэффициент полноты восстановления ресурса характеризу­ет возможность сокращения ресурса после ремонта, т. е. качест­во произведенного ремонта (0≤ η ≤1), После первого ремонта (между первым и вторым отказами) этот коэффициент равен

, после k-го отказа

Сокращение ресурса после первого и последующих ремонтов, которое необходимо учитывать при планировании и организации работ по обеспечению работоспособности, объясняется: частич­ной заменой только отказавших деталей в узле и агрегате, при значительном сокращении надежности других, особенно сопря­женных; использование запасных частей и материалов иного ка­чества, чем при изготовлении автомобиля, например, восстанов­ленных деталей; уровнем организации и технологии.

Ведущая функция потока отказов (функция восстановления)

Ведущая функция потока отказов

Рисунок 5.2 Определение ведущей

функции потока отказов

Ω(х) определяет накопленное количество первых и последующих отказов изделия к моменту (на­работке) х. Как следует из рис. 2.7, из-за вариации нарабо­ток на отказы происходит их смешение, а функции вероятностей первых и последующих отказов F₁, F₂,… , F_k частично на­кладываются друг на друга. Поэтому, если вероятное количе­ство отказов, например, к пробегу х₁ (см. рис. 2.7) определяется как Ω(x₁) =F₁(x₁) то для момента х₂ общее количество отказов определяется суммирова­нием вероятностей первого F₁(x₂) и второго F₂(x₂) отказов. Поэто­му Ω{x₂)=F₁(x₂) + F₂(x₂), а в общем виде:

Параметр потока отказов ω(х) — плотность вероятности воз­никновения, отказа восстанавливаемого изделия, определяемая для данного момента времени или пробега:

,

где f(x) — плотность вероятности возникновения отказа.

Иными словами, ω(х) — это относительное число отказов, приходящееся на единицу времени или пробега одного изделия. Причем при характеристике надежности изделия число отказов обычно относят к пробегу, а при характеристике потока отказов, поступающих для их устранения, — ко времени работы соответ­ствующих производственных подразделений. Следует отметить, что ведущая функция и параметр потока отказов определяются аналитически лишь для некоторых видов законов распределения. Например, для экспоненциального закона

; ; при η=1, ;

для нормального закона

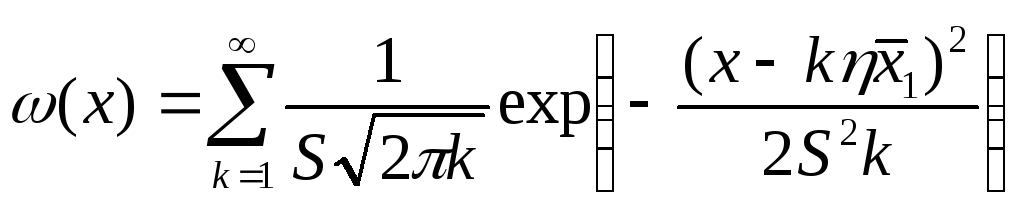
где Φ(z) – нормированная функция для ; k – число отказов (замен).

П р и м е р. Наработка до первой замены накладок сцепления составляет = 58 тыс. км, среднее квадратическое отклонение S =10 тыс. км, коэффици­ент восстановления ресурса т) = 0,6. Определить возможное число замен при пробеге автомобиля 150 тыс. км.

Для расчетов используем формулу (2.21), последовательно определяя F₁, F₂, F₃ и т. д.;

(приложение 2);

далее F₃(150) = 0,995; F₄(150) = 0,69; F₅(150) = 0,136; F₆(150) = 0,007.

Ввиду того, что F₆ мало, последующие расчеты для F₇ и других можно не производить. Таким образом, к пробегу 150 тыс. км возможное число замен данной детали составит .

Для практического использования важны некоторые прибли­женные оценки ведущей функции параметра потока отказов:

Из формулы (2.23) следует, что на начальном участке рабо­ты, где

F(x) << l, Ω(x) ≈ F(x).

Ведущая функция параметра потока отказов стареющих эле­ментов для любого момента времени или для пробега удовлетво­ряет следующему неравенству

.

Для рассмотренного выше примера с заменой накладок сцеп­ления, используя формулу 2.24, получим следующую оценку ве­дущей функции параметра потока отказов при пробеге автомо­биля х=150 тыс. км: 3,3 ≤ Ω(x) ≤ 4,3. Таким образом, к пробегу х в среднем будет наблюдаться от 3,3 до 4,3 отказов сцепления. Согласно более точным расчетам по формуле 2.21, эта величина составляет 3,83.

Для любого закона распределения наработки на отказ, имею­щего конечную дисперсию D = S², ведущая функция параметра потока отказов при достаточно большом значении х определяет­ся по следующей формуле

При расчете гарантированных запасов необходима интерваль­ная оценка ведущей функции параметра потока отказов (для до­статочно больших значений х)

,

где Z_α – нормированное отклонение для нормального закона распреде­ления при условии, что число отказов (замен) с вероятностью 1– α будет заключено в данных пределах

П р и м е р. Определить для условий предыдущего примера (x₁ = 58 тыс. км, η =0,6; S=10 тыс км) с достоверностью 1 – α = 0,9 необходимое число накла­док сцепления за пробег автомобиля 150 тыс. км. Так как условия задачи тре­буют обеспечение накладками с вероятностью 90%, то необходимо определить верхнюю границу потребности в накладках за 150 тыс. км пробега. Прежде всего определим нормированное отклонение при 1– α = 0,9 = Ф(Z_α). Из приложения 2 имеем Z_α =1,25. верхняя граница потребности в деталях со­ставит Ω(150)=5,04. Следовательно, с вероятностью 90% можно полагать, что за 150 тыс. км пробега потребуется не более 5 комплектов накладок сцеп­ления. Средний же расход составит около 3,8 комплектов.

Таким образом, используя значения параметра потока отка­зов, можно определить конкретный расход деталей за любой за­данный период и планировать работу системы снабжения.

Параметр потока отказов может быть оценен на основании экспериментальных данных (отчетных материалов, специальных наблюдений) следующим образом (см. рис. 2.6):

,

где т(х₁) – суммарное число отказов п автомобилей в интервале пробега от x₁ до х₂ (или времени работы от t₁ до t₂); Ω(x₁) и Ω(x₂) – ведущие функ­ции потока отказов к пробегу x₁, и х₂.

В общем случае параметр потока отказов непостоянен во вре­мени, т. е.

ω(t, x) ≠ const. Наблюдаются три основных случая поведения параметра во времени.

Первый случай (рис. 2.8, 1) – полное восстановление ресурса после каждого отказа, т. е. η_i = const. При этом происходит стабилизация параметра потока от­казов на уровне .

Второй случай (см. рис. 2.8, 2) – неполное, но постоянное восстановление ресурса после первого отказа, т. е. η_i <1; η_i = const. Для этого случая также характерна стабилизация параметра потока отказов, но на более высоком уровне, равном

.

Третий случай (см, рис. 2.8, 3) – последовательное снижение полноты восстановления ресурса, т. е. η_i ≠ const; 1 > η₁> η₂>... η_k.

В

Рисунок 5.3 Виды изменения параметра потока отказов

этом случае и параметр потока отказов непрерывно уве­личивается, что приводит к по­стоянному повышению нагрузки на ремонтные подразделения предприятия. Однако при расче­тах для этого случая можно принимать ω = const, как среднюю для отдельных периодов (например, х₂ – х₃; х₃ – х₄ и т. д., см. рис. 2.8), на которые разбивается весь пробег или время работы автомобиля. Подобный подход возможен также при анализе изме­нения параметра потока отказов в течение года. Этот параметр может приниматься практически постоянным для всех времен го­да: зимнего (ω_з), осенне-весеннего (ω_ов) и летнего (ω_л) пе­риодов.

Стабилизация параметра потока отказов позволяет рассмат­ривать потоки как простейшие или пуассоновские, обладающие рядом важных в прикладном плане свойств: стационарности, ординарности и отсутствия последствия.

Стационарным является поток отказов, при котором вероят­ность возникновения отказов в течение определенного промежут­ка времени (или пробега) зависит только от длины этого проме­жутка и не зависит от начала отсчета времени.

Для стационарного потока количество отказов за интервал х следующее:

Ординарность означает, что одновременное возникновение двух отказов у автомобиля практически маловероятно.

Отсутствие последствия – это независимость характера пото­ка от числа ранее поступивших отказов и моментов их возник­новения. На практике суммирование не менее 6–8 элементарных потоков приводит к образованию простейшего или близкого к нему потока.

Для простейшего потока отказов вероятность возникновения определенного числа отказов в течение времени определяется за­коном Пуассона:

,

где k = 0, 1, 2, ... – число отказов, возникающих за время t;

ω – пара­метр потока отказов.

В реальных условиях производства обычно фиксируют значе­ние t, например 1 ч, 1 смена, 1 неделя и так далее, т. е. t =1, а ωt = Ω° = a – среднее число отказов, возникающих за время t. В этом случае

Отказ, поступающий в зону ремонта для устранения, называ­ется требованием. В реальных условиях требование может включать комбинацию отказов и неисправностей агрегатов и автомобилей.

Используя формулу (2.30), можно установить вероятность появления определенного числа требований P_k при известном среднем значении а. Например, при а=3 вероятности равны (рис. 2.9. 2); отсутствие требований

1 – а = 1; 2 – а = 3; 3 – а = 6

Рисунок 5.3 Вероятность возникновения требований по закону Пуассона в зависимости от среднего их числа

или 5%; вероятность появления одно­го требования — 0,15; двух — 0,22; трех — 0,22; четырех — 0,16 и т. д. Таким образом, за­грузка постов и оборудования носит вероятностный характер: 22% от всех смен будет иметь фактическое число требований, совпадающее со средним, у 42% (5+15+22) загрузка будет меньше, а в 36% (100—22—42) случаев — больше средней.

Следовательно, расчет производственных помещений, обору­дования, штата рабочих, т. е. пропускной способности предприя­тия, исходя из средней потребности, может соответствовать не­полной загрузке зон и участков, или необходимости ожидания момента обслуживания, т. е. образованию очереди. В зависимо­сти от стоимости простоя автомобилей в ожидании ремонта (С_A), а также оборудования и рабочих в ожидании автомобилей (С_OP), требующих ремонта, определяют оптимальную пропускную спо­собность зон, участков, постов ТО и ремонта. Эта задача реша­ется с использованием теории массового обслуживания и из усло­вия минимизации выражения u = С_A + С_OP → min, называемого целевой функцией.

Характерным признаком закона Пуассона является равен­ство дисперсии среднему значению, поэтому коэффициент вариа­ции потока требований равен v = а^-1/2. Это означает, что с увели­чением программы вариация ее фактического значения сокра­щается:

Средняя программа ....................	1	2	3	4	5	9	25
Коэффициент вариации ...............	1	0,71	0,58	0,5	0,45	0,3	0,2

Закон распределения становится более симметричным (рис. 2.9, 3) с увеличением программы, что благоприятно сказывает­ся на организации технологического процесса ТО и ремонта. По­этому укрупнение предприятий, централизация и кооперирова­ние ТО и ремонта, приводящие к увеличению программ работы, является одним из направлений совершенствования технической эксплуатации автомобилей.