7. Магнитное поле тока

7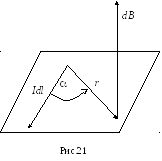.1. Закон Био-Савара-Лапласа: вектор индукции магнитного поля, созданного элементом тока, в точке, удаленной от элемента тока на расстояние:

• в векторной форме

;

• в скалярной форме

,

где – радиус-вектор, проведенный от элемента токадо той точки, в которой определяется индукция поля;– магнитная постоянная,– угол междуи(рис.21).

7.2. Принцип суперпозиции: при наложении магнитных полей магнитная индукция результирующего поля равна векторной сумме магнитных индукций, создаваемых каждым током и движущимся зарядом в отдельности:

.

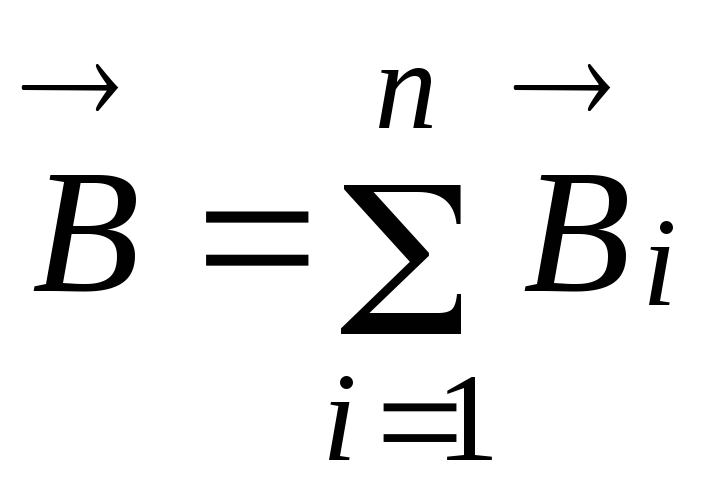7.3. Связь между величинами индукции магнитного поля В и напряженности Н в однородной среде:

В = ₀Н,

где -магнитная проницаемость среды; ₀–магнитная постоянная,

₀ = 410^-7 Гн/м.

7.4. Магнитная индукция:

• поля, создаваемого бесконечно длинным прямолинейным проводником с током на расстоянии r от оси проводника,

;

• поля в центре кругового тока радиусом R

;

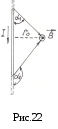
• поля, создаваемого отрезком прямолинейного проводника с током на расстоянии r₀ от проводника, (обозначения на рис.22):

;

• поля внутри бесконечно длинного соленоида () с токомI

,

где l – длина соленоида, d – диаметр соленоида, N – число витков соленоида, n – число витков на единицу длины соленоида.

7.4. Сила, действующая на проводник с током длиной l в однородном магнитном поле с индукцией В (сила Ампера):

F_A= I B l sin.

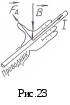
Направление силы определяется по правилу левой руки (применение правила левой руки показано на рис.23).

7.5. Сила взаимодействия двух прямых бесконечно длинных параллельных проводников с токами I₁ и I₂, находящихся на расстоянии d друг от друга, приходящаяся на отрезок провода длиной l ( l >> d ):

.

7.5. Магнитный момент контура с током:

,

где I – сила тока в контуре; S – площадь, охватываемая контуром; - вектор нормали к контуру;Р_m=IS – модуль вектора .

7.6. Механический момент, действующий на контур с током, помещенный в однородное магнитное поле с индукцией В:

или М = Р_mВsin,

где  - угол между векторами .

7.8. Сила, действующая на заряд q, движущийся в однородном магнитном поле с индукцией В со скоростью (сила Лоренца):

или F_л = qBsin.

Направление силы определяется по правилу левой руки, применение которого показано на рис.24.

7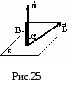.9. Магнитный поток однородного поляФ через плоский контур площадью S:

Ф = ВScos или Ф = В_nS,

где  - угол между вектором нормали к плоскости контура и вектором магнитной индукции ; В_n – проекция вектора индукции на нормаль к плоскости контура, В_n=Вcos (Рис.25).

7.10. Работа по перемещению замкнутого контура с током в магнитном поле:

,

где – изменение магнитного потока, пронизывающего поверхность, ограниченную контуром, при перемещении проводника.

7.11. Потокосцепление контура:

 = LI = NФ,

где L – индуктивность контура; I - сила тока в контуре; N – количество витков контура.

7.12. Закон электромагнитной индукции.

• Мгновенное значение электродвижущей силы, возникающей в проводящем контуре:

.

• Среднее значение ЭДС индукции:

,

где Ф = Ф₂ – Ф₁ - изменение магнитного потока за время t, N – число витков в контуре (например, в катушке).

• Мгновенное значение ЭДС самоиндукции, возникающей в замкнутом контуре с постоянной индуктивностью L при изменении в нем силы тока, если контур находится в неферромагнитной среде, для которой  = const:

.

• Среднее значение ЭДС самоиндукции:

.

7.13. Индуктивность бесконечно длинного соленоида (тороида):

L= ₀ n²V,

где n – число витков на единицу длины соленоида n = N/l; N – общее число витков; V – объем соленоида (V = Sl); S – площадь сечения соленоида; l – длина соленоида.

7.14 Энергия магнитного поля тока в контуре, обладающем индуктивностью :

.

7.15. Объемная плотность энергии магнитного поля (энергия, отнесенная к единице объема):

.