3. Динамика вращательного движения твердого тела

3.1. Момент силы и момент импульса

Различают момент силы относительно точки (точка О на рис. 3), называемая неподвижным началом или полюсом, и момент силы относительно оси.

Моментом силы относительно точки называется векторное произведение радиус-вектора , проведенного из этой точки (рис. 3), в точку приложения силына эту силу:

[ ]

Вектор перпендикулярен плоскости, в которой находятся векторыи.

Направление вектора определяется направлением векторного произведения векторови.

Модуль момента силы равен произведению модулей векторов ина синус угла α между ними:

М = rF sin α

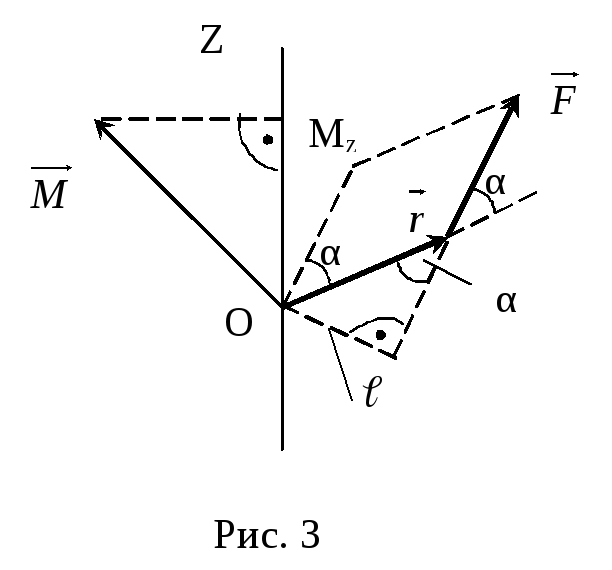
Модуль вектора может рассчитываться также как произведение модуля силына плечо (рис. 3):

М = F

Под плечом силы понимается кратчайшее расстояние между полюсом и линией действия этой силы.

Моментом силы относительно произвольной оси называется проекция момента силы относительно точки, находящейся на оси, на эту ось.

Моментом импульса материальной точки относительно неподвижного начала называется векторное произведение радиус-вектора , соединяющего неподвижное начало и движущуюся материальную точку, на импульс этой точки:

= [ ]

Вектор перпендикулярен плоскости, в которой находятся векторы и . Направление вектора определяется направлением векторного произведения векторови.

Модуль вектора момента импульса равен произведению модулей векторов ина синус угла между ними:

L = rPsin α

Моментом импульса относительно произвольной оси называется проекция момента импульса относительно точки, находящейся на оси, на эту ось.

Производная по времени t момента импульса материальной точки равна моменту сил, действующих на такую точку

Аналогичное утверждение справедливо и для системы тел или материальных точек, однако здесь под понимается момент импульса системы

,

а под - момент внешних сил,

,

действующих на такую систему:

3.2. Момент инерции твердого тела относительно данной оси:

,

где m_i и r_i - соответственно массы и расстояния материальных точек до оси вращения.

3.3. Моменты инерции относительно оси Z₀, проходящей через центр масс перпендикулярно плоскости основания:

сплошного цилиндра (диска) радиусом R и массой m

J_z0 = mR²;

полого цилиндра массой m, внутренним радиусом R₁ и внешним R₂

J_z0 = ;

тонкостенного полого цилиндра (обруча) массой m радиусами R₁R₂R

J_z0 = mR² .

Момент инерции шара массой m и радиусом R относительно оси Z₀, проходящей через центр масс

J_z0 = mR²

Момент инерции тонкого стержня массой m и длиной относительно осиZ₀, проходящей через центр масс стержня перпендикулярно его оси

J_z0 = m

3.4. Теорема Штейнера.

Момент инерции тела I относительно любой оси равен моменту его инерции I_c относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния d между осями:

.

3.5. Основное уравнение динамики вращательного движения.

Результирующий момент внешних сил относительно оси вращения z равен произведению момента инерции твердого тела относительно этой оси на угловое ускорение:

.

3.6. Момент импульса тела относительно оси вращения:

,

где I_z – момент инерции тела относительно оси вращения.

3.7. Закон сохранения момента импульса.

• Момент импульса в замкнутой системе тел сохраняется:

,

• в проекции на ось вращения z:

,

где - момент импульса i- го тела относительно оси вращения, т.е. проекция момента импульса i- го тела на ось вращения системы.

3.8. Кинетическая энергия тела, вращающегося относительно неподвижной оси:

.