Основные положения теории вероятностей

§ 1. Случайные события.

1. Пространство элементарных событий. Пусть при некотором фиксированном комплексе условий можно многократно повторить некоторый «эксперимент» или испытание. Если хотя бы некоторые из исходов таких испытаний будут различаться, то говорят об эксперименте со случайным исходом. Всевозможные результаты этих испытаний называются элементарными событиями ω. Совокупность всех элементарных событий Ω = {ω} называется пространством или множеством элементарных событий. Во многих случаях, но далеко не всегда, пространство элементарных событий конечно или хотя бы счётно. Например: множества элементарных исходов при бросании монеты или игральной кости – конечны; множество исходов в эксперименте, завершающимся выпадением «герба» в сколь угодно длинной серии бросания монеты – счётное; множество значений переменной x при мысленном бросании точки на отрезок [0;1] оси X (то есть, по сути, при выборе числа из этого интервала) – бесконечное и несчётное.

Любое подмножество A, B или C и т.д. множества элементарных событий называется случайным событием. Так как A Ì Ω, то для того, чтобы произошло событие A, должно осуществится хотя бы одно элементарное событие ωÎA.

Если заведомо известно (говорят «априори»), что в результате испытания произойдёт некоторое событие A, то такое событие называют достоверным; если событие A заведомо не произойдёт при осуществлении данного опыта, то оно называется невозможным.

Очевидно, само множество элементарных событий является достоверным событием. Невозможные события обычно обозначают символом Æ, означающим также пустое множество.

Операции над событиями. Рассматривая случайные события как подмножества множества Ω (оно же – достоверное событие) с обязательным добавлением невозможного события (пустого множества) Æ, можно утверждать:

— A Ì B, если из осуществления события A следует осуществление события B, или событие A влечёт за собой событие B;

— A = B и эти события называют эквивалентными, если одновременно выполняются условия A Ì B и B Ì A;

— событие Ā называется дополнением события A или противоположным событию A и осуществляется тогда, когда не происходит событие A;

— события называются совместными, если они могут происходить одновременно, и несовместными, если это не так (если речь идёт о совместности более, чем двух событий, то для каждой пары этой совокупности событий применяют термин попарной совместности или несовместности, оставляя для всей совокупности термин совместность или несовместность в совокупности; очевидно, совместные в совокупности события будут и попарно совместны, но обратное утверждение неверно);

— события называются независимыми, если наступление какого либо из них не зависит от того, наступили или нет ранее другие события из рассматриваемого множества событий; здесь также различают попарную независимость и независимость в совокупности и также первая не влечёт за собой вторую;

— объединением или суммой двух событий A и B называется событие C, состоящее в том, что произошло хотя бы одно из событий A или B: C = A U B или C = A + B; операцию объединения легко обобщить на произвольное число событий: событие состоит в том, что происходит хотя бы одно из событийA₁, A₂, . . . , A_n.

— пересечением или произведением двух событий A и B называется событие C, состоящее в том, что произошли оба события A и B: C = A ∩ B или C = A • B; операцию пересечения легко обобщить на произвольное число событий: событие состоит в том, что происходят одновременно все события A₁, A₂, . . . , A_n.

— разностью двух событий A и B называется событие C, состоящее в том, что событие A происходит, а событие B не происходит (или наоборот): C = A\ B (C = B \ A);

— множество событий { A₁, A₂, . . . , A_n }называется системой событий, если это множество не содержит ни одной пары эквивалентных событий; эта система будет называться системой несовместных событий, если все события в ней попарно несовместны; наконец, система несовместных событий называется полной, если сумма всех событий в системе является достоверным событием Ω.

Кроме того, необходимо отметить, что операции объединения (суммы) и пересечения (произведения) коммутативны и ассоциативны, то есть

A U B = B U A; A ∩ B = B ∩ A и (A U B) U C = A U (B U C); (A ∩ B) ∩ C = A ∩ (B ∩ C), а также эти операции взаимно дистрибутивны:

A U (B ∩ C) = (A U B) ∩ (A U C); A ∩ (B U C) = (A ∩ B) U (A ∩ C).

Из определения разности событий следует и из того, что , следует:

A\B = A ∩= ∩ A = ∩ = \ ; Ω\A = Ω ∩ Ā = Ā.

В теории вероятностей и её приложениях важную роль играет так называемый принцип двойственности, который можно выразить соотношениями:

∩.

К принципу двойственности следует отнести ещё одно соотношение:

2. Классическое определение вероятности. Пусть в результате некоторого эксперимента событие A может произойти или не произойти. Если выполнено N экспериментов и в результате событие A произошло n раз, то число ν(A) = n ⁄ N называется частотой появления события A. Если при увеличении N частота ν(A)сходится к некоторому постоянному значению, то говорят об устойчивости частоты или статистической устойчивости. Теория вероятностей основана на системе аксиом, которые опираются на экспериментальные факты, в частности на статистическую устойчивость. Величину P(A), к которой стремится частота ν(A) при увеличении N, называют вероятностью события А. Очевидно, что так определённая вероятность удовлетворяет следующим условиям: 0 ≤ P(A) ≤ 1, причём P(Æ) = 0 и P(Ω) =1, то есть вероятность невозможного события равна нулю, а вероятность достоверного события равна единице.

Элементы комбинаторики. В комбинаторике рассматриваются различные виды соединения элементов. Допустим, что требуется выполнить одно за другим k действий. Если первое действие можно выполнить n₁ способами, второе – n₂ способами, третье – n₃ способами и так до k-го действия, которое можно выполнить n_k способами, то все k действий вместе могут быть выполнены (n₁·n₂·n₃·...·n_k) способами; в этом заключается основной принцип комбинаторики (правило умножения).

Пусть– множество изn элементов. Произвольное m-элементное подмножество из n элементов называется сочетанием из п элементов по т. Сочетания из n элементов по m различаются составом элементов; их возможное число равно:

Сочетания с повторениями также различаются составом элементов, но элементы в них могу повторяться до m раз. Число различных сочетаний с повторениями из n элементов по m равно:

Множество называется упорядоченным, если каждому его элементу поставлено в соответствие некоторое число (номер элемента) от 1 до n (n – число элементов множества) так, что разным элементам соответствуют различные числа. Различные упорядоченные множества, которые отличаются лишь порядком элементов (то есть могут быть получены из того же самого множества), называются перестановками этого множества. Перестановки п элементов различаются их порядком; число возможных перестановок равно: P = 1·2·3·…·n! .

Перестановка с повторениями элементов, причём один из элементов повторяется α раз, другой – β раз, наконец, последний – γ раз, характеризуется возможным числом

В частности, при разбиении множества из n элементов на т не имеющих общих элементов подмножеств с k₁, k₂, …, k_т элементами соответственно (то есть k₁+ k₂+ …+ k_т = п), число таких разбиений задаётся полиномиальными коэффициентами

Рассмотрим теперь упорядоченные подмножества данного множества изn элементов. Само множество считается неупорядоченным, поэтому каждое каждое его подмножество может быть упорядочено каким-либо возможным способом. Число всехk-элементных подмножеств множества равно; каждое такое подмножество можно упорядочитьk! способами и таким образом получим все упорядоченные k-элементные подмножества множества . Упорядоченныеk-элементные подмножества множества из n элементов называется размещениями из n элементов по k, они различаются и составом элементов и их порядком. Возможное число таких размещений

Возможное число размещений с повторениями по k из n элементов R_повт.= n^k.

Пусть n-элементное множество A является суммой множеств A₁, A₂, …, A_k, число элементов которых равно соответственно n₁, n₂, …, n_k (﴿. При этом B – m-элементное подмножество множества A, содержащее m₁ элементов из A₁, m₂ из A₂, … , m_k элементов из A_k (). Число способов, которыми можно выбрать такое множествоB из A (множества неупорядоченные) в силу основного принципа комбинаторики равно

.

Геометрическая вероятность. Допустим, что в результате опыта в некоторой области Ω наудачу появляется точка ω. Требуется определить вероятность P(A) того, что ωÎA, где А – область, принадлежащаяΩ, то есть A Ì Ω. По определению полагают P(A) = m(A) / m(Ω), где m(A) и m(Ω) – мера области А и области Ω, под которой следует понимать длину, площадь, объём в одно-, двух- и трёхмерном случаях соответственно.

3. Условная вероятность; независимость событий; фрмулы сложения и умножения вероятностей; формулы полной вероятности и Байеса. Если мы имеем дело с зависимыми событиями А и В, то рассматривают так называемые условные вероятности Р(А/В) и Р(В/А), то есть вероятность наступления события А при условии того, что уже произошло событие В и наоборот. Таким образом, если P(A)= Р(А/В), то события А и В независимые, а если P(A) ≠ Р(А/В), то события А и В зависимые. Так как В – результат опыта, то P(A) называют доопытной или априорной вероятностью, а Р(А/В) – послеопытной или апостериорной вероятностью.

При расчёте вероятностей различных событий используются следующие соотношения:

— формула сложения вероятностей: P(A U B) = P(A) + P(B)– P(A∩B); поскольку для несовместных событий А ∩B = Æ, то для них P(A + B) = P(A) + P(B); и втом и в другом случаях в результате определяется вероятность того, что произойдёт или событие А или событие В, причём в первом случае они могут произойти и одновременно; обобщение на случай произвольного конечного числа событий: вероятность того, что произойдёт хотя бы одно из событий A₁, A₂, . . . , A_n равна для несовместных событий и

для совместных событий;

— формула умножения вероятностей: вероятность того, что в результате опыта произойдут оба зависимых события А и В равна: P(A∩B) = P(A)·P(B/A) = P(B)· P(A/B); если события А и В независимые, то P(A·B) = P(A)· P(B); обобщение этих формул на случай произвольного конечного числа событий имеет следующий вид: вероятность того, что произойдёт каждое из событий A₁, A₂, . . . , A_n равна для независимых событий идля зависимых;

— формула полной вероятности: пусть H₁, H₂, . . . , H_m – полная группа несовместных событий, называемых обычно гипотезами, и событие А совместно хотя бы с некоторыми из этих событий, то есть не все условные вероятности P(A/H_j), j = 1,2, …,m , равны нулю; тогда вероятность наступления события А равна: , гдеP(H_j) понимается как априорная вероятность наступления гипотезы H_j, j = 1,2,…,m , а P(A/H_j) – как вероятность наступления события А при выполнении этой гипотезы;

— формула Байеса: для той же полной группы несовместных событий – гипотез H₁, H₂, . . . , H_m может представлять интерес вопрос о том, как изменятся вероятности гипотез после того как наступило событие А (т. е. каковы апостериорные вероятности гипотез); возможность такого перерасчёта позволяет формула:

.

4. Повторение испытаний; формула Бернулли. Пусть вероятность появления события А при единичном испытании P(A) = p. Опыт повторяется при некотором фиксированном комплексе условий n раз, т.е. осуществляется серия из n независимых испытаний. Вероятность того, что в сериип испытаний событие А наступит ровно т раз (наступит т «успехов»), определяется по формуле Бернулли

, т = 1,2, … , п, (1.1)

где q = (1 – p) – вероятность наступления противоположного события Ā при однократном испытании.

Совокупность чисел, определяемых формулой (1) при заданных п и р, называется биномиальным распределением вероятностей.

Значение т = т₀, при котором вероятность (1) принимает наибольшее значение, называется наивероятнейшим числом «успехов». Это число принимает значения в единичном интервале p(n+1) – 1 ≤ m₀≤ p(n+1); это единственное значение m₀ = [p(n+1)] при условии, что p(n+1) – дробное число (здесь […] – целая часть числа), и два числа (границы интервала), если p(n+1) – целое число.

Если в результате каждого из n независимых испытаний может произойти одно из k попарно несовместных событий A_1, A_2, …, A_k с вероятностями p_1, p_2, …, p_k соответственно (p₁+ p₂+ …+ p_k = 1), то вероятность наступления m₁ раз события A₁, m₂ раза – события A₂, …, m_k раз – события A_k , причём m₁+ m₂+…+ m_k = n, определяется равенством, задающим полиномиальное распределение вероятностей

(1.2)

Пусть дана совокупность N объектов, среди которых M отмеченных (например бракованных изделий, белых шаров, выигрышных билетов и т.п.). Извлекается наугад n объектов; требуется определить вероятность P(n,m) того, что среди них окажется m отмеченных. Если производить извлечение с возвращением после каждого опыта объектов в общую совокупность с последующим перемешиванием, то получается вероятностная схема Бернулли с p=M/N и числом опытов n. Извлечение без возвращения даёт так называемое гипергеометрическое распределение

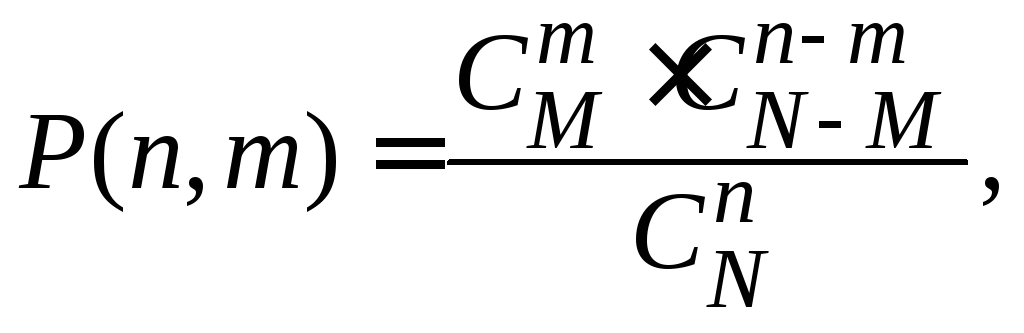(1.3)

где – число способов извлечьm объектов из M отмеченных; – число способов выбораn объектов из совокупности N различных объектов; – соответствующее число способов добратьn – m объектов до общего числа n, выбирая их из N – M не отме-ченых.

Приближённая формула Пуассона; теоремы Муавра – Лапласа. При больших значениях п (~ 10÷10² и более) для биномиального распределения справедливы следующие асимптотические соотношения (тем более точные, чем больше п):

а) при n → ∞ и p → 0 так, что np → λ = const справедлива асимптотика Пуассона

; , (1.4 – 1.5)

в) при n → ∞ и p – немалой (практически, при p ≥ 0,1 , а точнее при npq > 9) справедливы: локальная теорема Муавра – Лапласа

где , (1.6)

а также интегральная теорема Муавра – Лапласа

где . (1.7 – 1.8)

Вероятность того, что относительная частота k/n события A в серии n независимых испытаний отличается от вероятности этого события в отдельном испытании p по абсолютной величине не более чем на ε>0, равна

. (1.9)

Приближённые формулы (5) и (7) справедливы и при условии, что входящие в них неравенства являются строгими. Вычисления по формулам (4 – 7; 9) производятся с применением таблиц II – IV приложения.

Практическая работа I

З а д а н и я

Вариант 1.

1. Доказать, что если события A и B независимы, то события A и,и B, итакже независимы.

2. Бросаются две игральные кости. Определить вероятность того, что: а) сумма числа очков не превосходит N = 8; б) произведение числа очков не превосходит N = 16; в) произведение числа очков делится на N = 4.

3. Слово ВЕРОЯТНОСТЬ составлено из карточек, на каждой из которых написана одна буква. Затем карточки смешивают и вынимают наугад без возврата по одной. Найти вероятность того, что из вынутых по порядку букв составится первоначальное слово.

4. В квадрат с вершинами (0;0), (0;1), (1;0), (1;1) наудачу брошена точка. Пусть (ξ;η) – её координаты. Найти вероятность того, что корни уравнения x² + ξ·x + η = 0 – действи-тельные .

5. В двух партиях k₁ = 71% и k₂ = 47% доброкачественных изделий соответственно. Наудачу выбирают по одному изделию из каждой партии. Какова вероятность обнаружить среди них: а) хотя бы одно бракованное; б) два бракованных; в) одно доброкачественное и одно бракованное.

6. В одной урне 5 белых и 6 чёрных шаров, а в другой – 4 белых и 8 чёрных шаров. Из первой урны случайным образом вынимают 3 шара и опускают во вторую урну. После этого из второй урны также случайно извлекают 4 шара. Найти вероятность того, что все шары, вынутые из второй урны – белые. Оценить, при таком исходе, вероятность того, что на первом этапе из первой урны извлекли 3 чёрных шара.

7. Монета бросается до тех пор, пока герб не выпадет n = 3 раза. Определить вероятность того, что цифра выпадет m = 5 раз.

8. Имеется общество из n = 500 человек. Найти вероятность того, что у двух человек день рождения придётся на Новый год. Вероятность рождения в фиксированный день полагать равной p = 1 / 365.

9. Какова вероятность того, что в столбике из 100 наугад отобранных монет будет от 45 до 55 монет, расположенных «гербом» вверх.

Вариант 2.

1. Пусть A, B, C – случайные события. Каков смысл равенств: а) A·B·C = =A; б) AUBUC = A.

2. Бросаются две игральные кости. Определить вероятность того, что на верхних гранях появятся следующие числа очков: а) только нечётные; б) сумма которых чётна; в) сумма которых больше, чем их произведение.

3. Имеются изделия четырёх сортов, причём число изделий i -го сорта (i = 1, 2, 3, 4) равно n_i (n₁ = 2; n₂ = 3; n₃ = 4: n₄ = 2 соответственно). Определить вероятность, что среди них m₁ = 1 первосортных, m₂ = 2, m₃ = 3 и m₄ = 1 второго, третьего и четвёртого сорта соответственно (m₁ + m₂ + m₃ + m₄ = m).

4. В квадрат с вершинами (0;0), (0;1), (1;0), (1;1) наудачу брошена точка. Пусть (ξ;η) – её координаты. Найти вероятность того, что ξ + η ≤ 1.

5. В урне 6 белых и 5 чёрных шаров. Из урны случайно извлекают 4 шара. Найти вероятность того, что среди них имеются: а) 2 белых шара; б) меньше двух белых шаров; в) хотя бы один белый шар.

6. Имеется три партии микросхем общей численностью n = 1000 штук, причем n₁ = 160 и n₂ = 570 в первой и второй партиях. В первой партии 6%, во второй – 5%, а в третьей – 4% бракованных изделий. Наудачу из общего количества выбирается одна микросхема. Какова вероятность, что она – бракованная? Какова вероятность, что эта микросхема принадлежит третьей партии изделий?

7. Вероятность выигрыша по лотерейному билету равно p = 0,3. Куплено n = 13 билетов. Найти наивероятнейшее число выигравших билетов и соответствующую вероятность.

8. На телефонной станции неправильное соединение происходит с вероятностью p = 0,005. Найти вероятность того, что среди n = 200 соединений произойдет: а) одно неправильное; б) менее 3-х неправильных; в) более 2-х неправильных соединений.

9. В каждом из n = 600 независимых испытаний событие A происходит с постоянной вероятностью p = 0.85. Найти вероятность того, что относительная частота m/n этого события по модулю от вероятности более чем на: а) ε₁ = 0,0055; б) ε₂ = 0,011.

Вариант 3.

1. Пусть события A и B₁ независимы и независимы также события A и B₂, при этом B₁∩B₂ = Ø. Доказать, что события A и B₁+B₂ независимы.

2. Бросаются три игральные кости. Определить вероятность того, что на верхних гранях появятся следующие числа очков: а) только чётные; б) которые все одинаковы; в) произведение которых делится на их сумму.

3. Слово АПЕЛЬСИН составлено из карточек, на каждой из которых написана одна буква. Затем карточки смешивают и вынимают наугад без возврата по одной. Найти вероятность того, что из вынутых по порядку букв составится слово СПАНИЕЛЬ.

4. В квадрат с вершинами (0;0), (0;1), (1;0), (1;1) наудачу брошена точка. Пусть (ξ;η) – её координаты. Доказать, что для 0 ≤ x; y ≤ 1 P{ξ < x; η < y}=P{ξ < x}· P{η < y}= xy.

5. Сколько раз надо бросить пару игральных костей, чтобы с вероятностью не менее 0,5 хотя бы однажды выпало одинаковое число очко на костях?

6. В трёх урнах содержатся шары: в первой – 2 белых и 3 чёрных; во второй – 2 белых и 2 чёрных; в третьей – 3 белых и 1 чёрный шар. Из первой урны наугад переложен шар во вторую. После этого также перекладывают шар из второй урны в третью и, наконец, перекладывают шар из третьей урны в первую. Какой состав шаров в первой урне после этого наиболее вероятен? Определить вероятность того, что состав шаров во всех урнах останется без изменений.

7. Наблюдениями установлено, что в некоторой местности в сентябре в среднем бывает 12 дождливых дней. Какова вероятность, что из случайно выбранных в этом месяце 8 дней 3 дня окажутся дождливыми?

8. На телефонной станции неправильное соединение происходит с вероятностью p = 0,004. Найти вероятность того, что среди n = 100 соединений произойдет: а) два неправильное; б) менее 4-х неправильных; в) более 3-х неправильных соединений.

9. Производство даёт 1% брака. Какова вероятность того, что из взятых на исследование 1100 изделий выбраковано будет не более 17?

Вариант 4.

1. Доказать, что если события A и B – независимы, то они совместны.

2. Бросаются четыре монеты. Определить вероятность того, что : а) только на одной монете появится герб; б) хотя бы на одной монете появится герб; в) ни на одной монете не появится герб.

3. Монеты общим количеством 20 штук, среди которых 10 – достоинством в 1 руб.; 5 – достоинством в 2 руб.; 3 – достоинством в 5 руб. и остальные номиналом по 10 руб., раскладываются случайным образом на четыре кучки. Какова вероятность того, что в каждой кучке окажутся монеты одного номинала.

4. В квадрат с вершинами (0;0), (0;1), (1;0), (1;1) наудачу брошена точка. Пусть (ξ ; η) – её координаты. Определить вероятность P{|ξ – η| < 1/3}.

5. Сколько раз надо бросить пару игральных костей, чтобы с вероятностью не менее 0,9 хотя бы однажды на костях выпало 8 очков?

6. Три орудия производят стрельбу по трём целям. Каждое орудие выбирает себе цель случайным образом и независимо от других. Цель, обстрелянная одним орудием, поражается с вероятностью p. Определить вероятность того, что из трёх целей будут поражены только две. Если такое произошло, то как изменится оценка вероятности того, что были обстреляны все три цели (оценить эту величину в общем случае и при p = 0,6)?

7. Что вероятнее, выиграть у равносильного противника: 1) три партии из четырёх или пять из восьми? 2) не менее трёх партий из четырёх или не менее пяти партий из восьми?

8. Средняя плотность болезнетворных микробов в одном кубическом сантиметре воздуха равна 100. Берётся на пробу 2 дм³ воздуха. Найти вероятность того, что в нём будет обнаружен хотя бы один микроб.

9. Всхожесть семян данного растения равна 0,9. Найти вероятность того, что из 900 посаженных семян число проросших будет заключено между 790 и 890.

Вариант 5.

1. Пусть события A, B и С – произвольные случайные события. Выразить через операции с этими событиями события, состоящие в том, что: а) произошло, по крайней мере, два из этих событий; б) произошло два и только два из этих событий; в) произошло не больше двух из этих трёх событий.

2. Бросаются три игральные кости. Определить вероятность того, что на верхних гранях появятся следующие числа очков: а) сумма числа очков не более 16; б) произведение числа очков не менее 16; в) произведение числа очков делится на 16.

3. В лифт семиэтажного дома на первом этаже вошли 3 человека. Каждый из них с одинаковой вероятностью выходит на любом этаже, начиная со второго. Наити вероятности событий: A = {все пассажиры выйдут на седьмом этаже}; B = {все пассажиры выйдут на одном и том же этаже}; C = {все пассажиры выйдут на разных этажах}.

4. На отрезок [a;b] длиной l случайным образом бросаются две точки Какова вероятность того, что расстояние между ними не превзойдёт числа λ (0 ≤ λ ≤ l).

5. Вероятность попадания в цель для первого стрелка равна 0,7, а для второго – 0,8. Стрелки выстрелили одновременно. Какова вероятность того, что лишь один из них попадёт в цель? Какова вероятность того, что первый стрелок попадёт в цель?

6. В пирамиде стоят без определённого порядка 18 винтовок, 3 из которых с оптическим прицелом. Стрелок, стреляя из винтовки с оптическим прицелом, поражает мишень с вероятностью 0,9 , а стреляя из винтовки без оптического прицела – с вероятностью 0,75. Какова вероятность того, что стрелок поразит мишень стреляя из случайно взятой винтовки? Если мишень поражена, то какова вероятность того, что это сделано из винтовки с оптическим прицелом.

7. При въезде в новую квартиру в осветительную сеть было включено 2k новых электролампочек. Каждая из них в течении года перегорает с вероятностью p. Найти вероятность того, что в течении года не менее половины первоначально включенных ранее лампочек придётся заменить новыми. Оценить эту вероятность в общем виде и найти её значение для k = 9 и p = 0,1.

8. Вероятность того, что любой абонент позвонит на коммутатор в течении часа, равна 0,01. Коммутатор обслуживает 800 абонентов. Определить вероятность того, что в течении часа позвонит от 5 до 7 абонентов.

9. Сколько нужно произвести опытов с бросанием монеты, чтобы с вероятностью 0,92 можно было ожидать отклонение частоты выпадения «герба» от теоретической вероятности 0,5 на абсолютную величину, меньшую чем 0,01?

Вариант 6.

1. Доказать, что три события образуют полную группу

событий.

2. На шахматную доску из 64 клеток ставятся наудачу две ладьи (чёрная

и белая). Какова вероятность того, что они не «бьют» друг друга? (В шахматах ладья какого-либо цвета, чёрная или белая, будет иметь под «ударом» ладью противника, т. е. другого цвета, если та стоит на клетках одной горизонтали или одной вертикали с ней ).

3. При наборе телефонного номера абонент забыл две последние цифры и набрал их на удачу, помня только, что эти цифры нечётные и разные. Найти вероятность того, что номер набран правильно

4. Какой толщины должна быть монета, чтобы вероятность события {монета встала на ребро} была бы равна 1/3 ?

5. Имеется группа из k космических объектов, каждый из которых независимо от других обнаруживается радиолокационной станцией с вероятностью p. За группой объектов ведут наблюдения независимо друг от друга m радиолокационных станций. Найти вероятность того, что не все объекты группы будут обнаружены.

6. На вход радиолокационного устройства с вероятностью p поступает смесь полезного сигнала с помехой, а с вероятностью (1- p) – только одна помеха. В первом случае устройство регистрирует наличие какого-то сигнала с вероятностью p₁, а во втором – с вероятностью p₂. Найти вероятность того, что устройство зарегистрирует наличие какого-то сигнала, и какова при этом вероятность, что в его составе имеется полезный сигнал.

7. Изделия некоторого производства содержат 5% брака. Найти вероятность того, что среди десяти взятых наугад изделий: а) нет ни одного испорченного; б) будут два испорченных; в) будет менее трёх испорченных.

8. Прядильщица обслуживает 1000 веретён. Вероятность обрыва нити на одном веретене в течение одной минуты равна 0,004. Найти вероятность того, что в течение одной минуты обрыв произойдет: а) хотя бы на одном веретене; б) на двух веретёнах.

9. В первые классы школы принимают 200 детей. Определить вероятность того, что среди них окажется 100 девочек, если вероятность рождения мальчика равна 0,515.

Вариант 7.

1. Доказать, что .

2. Из последовательности чисел 1, 2, …, n наудачу выбираются два числа. Какова вероятность того, что одно из них меньше k, а другое больше k, где 1< k < n– произвольное целое число.

3. Вероятность того, что цель поражена при одном выстреле первым стрелком, равна p₁ = 0,66, вторым – p₂ = 0,49. первый сделал n₁ = 3, второй – n₂ = 2 выстрела. Определить вероятность того, что цель не поражена.

4. В отрезке единичной длины наудачу появляется точка. Определить вероятность того, что расстояние от точки до концов отрезка превосходит величину 1/3.

5. Два охотника стреляют в волка, причём каждый делает по одному выстрелу. Какова вероятность попадания в волка хотя бы одним из охотников, если вероятность попадания в цель для первого охотника равна 0,8 , а для второго – 0,7 ? Как изменится результат, если охотники сделают по два выстрела ?

6. Предположим, 5% всех мужчин и 25% всех женщин – дальтоники. Какова вероятность того, что наугад выбранное лицо страдают дальтонизмом? Какова вероятность того, что это мужчина? (Считать, что мужчин и женщин одинаковое число).

7. (З а д а ч а Б а н а х а) Некий курящий математик носит с собой две коробки спичек. Каждый раз, когда он хочет достать спичку, он выбирает наугад одну из коробок. Найти вероятность того, что когда математик вынет первый раз пустую коробку, в другой коробке окажется r спичек; 1 ≤ r ≤ n, где n – первоначальное число спичек в каждой коробке.

8. В опытах Резерфорда с α – излучением радиоактивное вещество испускало в среднем 3,87 α-частиц за 7,5 секунд. Найти вероятность того, что за 1 с это вещество испустит хотя бы одну α-частицу.

9. Вероятность рождения мальчика равна 0,515 , а девочки 0,485. В некоторой семье шестеро детей. Найти вероятность того, что среди них не больше двух девочек.

Вариант 8.

1. Пусть события A, B и С – произвольные случайные события. Выразить через операции с этими событиями события, состоящие в том, что: а) произошло по крайней мере одно из этих событий; б) произошло одно и только одно из этих событий; в) произошло только A.

2. В секретном замке на общей оси 4 диска, каждый из которых разделён на 10 секторов, содержащих различные цифры от 0 до 9. Замок открывается лишь в том случае, когда диски установлены так, что цифры на них образуют определённое четырёхзначное число. Найти вероятность того, что при произвольной установке дисков замок откроется.

3. По линии связи, имеющей 4 приёмнопередающих пункта, передаётся сообщение. На первом пункте происходит искажение сообщения с вероятностью 0,1. На каждом последующем пункте вероятность искажения возрастает на 0,05. Какова вероятность получения неискажённого сигнала?

4. В круг радиуса R вписан квадрат. Какова вероятность того, что поставленные наудачу внутри круга 2 точки окажутся внутри квадрата: а) обе; б) хотя бы одна из них.

5. Сколько раз нужно бросить игральную кость, чтобы с вероятностью, не меньшей: а) 0,5; б) 0,9 , хотя бы один раз выпало шесть очков ?

6. При помещении в урну тщательно перемешанных n шаров (m белых и n – m чёрных) один шар неизвестного цвета затерялся. Из оставшихся в урне n – 1 шаров наудачу извлекают один. Какова вероятность, что вынутый шар окажется белым ? Если так и произошло, то какова вероятность того, что затерялся белый шар?

7. Вероятность получения удачного результата при проведении сложного эксперимента равна 2/3. Найти наивероятнейшее число удачных опытов, если всего их было проведено 7.

8. Изготовитель отправил торговому предприятию 5000 изделий. Вероятность повреждения каждого изделия в пути равна 0,0002. Какова вероятность того, что предприятие получит не более 3-х повреждённых изделий?

9. Вероятность появления положительного результата в каждом из n испытаний равна 0,9. Сколько нужно произвести опытов, чтобы с вероятностью не меньшей 0,98 можно было ожидать, что не менее 150 опытов дадут положительный результат?

Вариант 9.

1. Последовательно бросают три монеты. Рассмотрим события A = {выпадение «герба» на первой монете} и B = {выпадение хотя бы одной «решётки»}. Определить, зависимы ли эти события и, если зависимы, то как?

2. На пяти карточках написаны цифры: 1, 2, 3, 4, 5. Вынимается одна карточка и записывается стоящее на ней число, после чего карточка кладётся обратно и смешивается с остальными. Затем вынимается вторая карточка и число, стоящее на ней, сравнивается с ранее записанным числом. Определить вероятности следующих событий: A – второе число больше первого; B – оба числа одинаковы; C – второе число меньше первого.

3. Батарея, состоящая из k орудий, ведёт огонь по r целям (k < r). Каждое орудие выбирает себе цель случайно и независимо от других. Найти вероятность того, что все орудия будут стрелять: а) по разным целям; б) по одной и той же цели.

4. Двое договорились о встрече в определённом месте между двумя и тремя часами дня. Тот, кто пришёл первым, ждёт другого в течение 15 минут, после чего уходит. Чему равна вероятность их встречи, если приход каждого из них в течение указанного часа может произойти в любое время? (Указание: обозначить моменты прихода лиц через x и y и рассматривать их как декартовы координаты на плоскости)

5. Прибор состоит из трёх узлов. В первом узле n₁ элементов, во втором n₂ и в третьем n₃. Узел Ι включён последовательно с блоком дублирующих друг друга и потому соединённых параллельно узлов ΙΙ и ΙΙΙ. Надёжность (вероятность безотказной работы) каждого элемента в любом из узлов одинакова и равна p. Выход из строя одного элемента означает выход из строя всего узла. Элементы выходят из строя независимо друг от друга. Найти надёжность прибора P.

6. Если позволяет погода, лётчик сажает самолёт на аэродром, наблюдая за ним визуально, и вероятность благополучной посадки при этом равна p₁. В условиях низкой облачности лётчик сажает самолёт вслепую по приборам. Надёжность приборов слепой посадки равна P и, если они работали нормально, самолёт садится благополучно с той же вероятностью p₁. Если приборы слепой посадки отказали, то вероятность благополучной посадки самолёта очень мала и равна p*. Найти: а) полную вероятность благополучной посадки самолёта, если в k% всех случаев посадки аэродром затянут низкой облачностью; б) вероятность того, что при благополучном приземлении самолёта лётчик пользовался приборами слепой посадки.

7. Баскетболист бросает мяч в корзину до первого попадания, но делает не более 6 бросков. Определить вероятность того, что число бросков будет не менее 4.

8. Оценить число бракованных изделий в партии из 1000 изделий, если вероятность обнаружить хотя бы одно бракованное среди 10 отобранных для контроля изделий не превосходит 0,1.

9. Игральную кость бросают 80 раз. Найти приближённо границы, в которых число m выпадений шестёрки будет заключено с вероятностью 0,9973.

Вариант 10.

1. Пусть события A, B и С – произвольные случайные события. Каков смысл равенств: A∩B∩С = BUС и AUBUС = A и возможно ли их одновременное выполнение?

2. На 10 карточках написаны цифры от 0 до 9. Карточки перевёрнуты и тщательно перемешаны. Две из них извлекаются наугад и укладываются на стол в порядке появления, затем читается полученное двухзначное число. Найти вероятность, что число будет: а) чётным; б) делится на 4. Как изменятся эти вероятности, если из карточек выкладывать трёхзначное число?

3. (Преферанс) Колода из 32 карт (от семёрок до тузов) раздаётся на три игрока (по 10 карт каждому) и ещё 2 карты остаётся в прикупе. Один из игроков видит, что у него на руках 6 карт бубновой масти, (что, при взятии игры на себя, позволить объявить эту масть козырной). Беря игру на себя, игрок сбрасывает две из 4-х карт других мастей и берёт две из прикупа. Какова вероятность того, что в прикупе две карты бубновой масти? Хотя бы одна?

4. Стержень длины l сломали на три части, выбирая наудачу места разлома. Найти вероятность того, что из получившихся трёх частей можно составить треугольник. (Указание: если x и y – длины двух из этих частей, то для того, чтобы можно было составить треугольник, необходимо выполнение неравенств x, y < l /2; x + y > l /2).

5. Студент пришёл на зачёт, зная из 30 вопросов только 24. Какова вероятность сдать зачёт, если после отказа отвечать на вопрос преподаватель задаёт ещё один вопрос?

6. В группе из 10 студентов, пришедших на экзамен, 3 подготовились отлично, 4 – хорошо, 2 – посредственно и 1 – плохо. В экзаменационных билетах 20 вопросов и отлично подготовленный студент может ответить на все из них, хорошо подготовленный – на 16, посредственно – на 10, плохо – на 5. Какова вероятность, что выбранный наудачу из этой группы студент ответит на три произвольно заданных вопроса? Если это произошло, то найти вероятность того, что студент подготовлен: а) отлично; б) плохо.

7. На пути движения автомобиля 6 светофоров, каждый из которых может остановить автомобиль с вероятностью 0,8. Определить вероятность того, что автомобиль пройдёт не менее 3-х светофоров до первой остановки.

8. Изделия некоторого производства содержат 2,5% брака. Найти вероятность того, что среди 200 взятых наугад изделий: а) нет ни одного испорченного; б) будет не более одного испорченного.

9. Вероятность появления успеха в каждом из 625 независимых испытаний равна 0,8. Найти вероятность того, что частота появления успеха отклонится по абсолютной величине от его вероятности не более, чем на 0,04.

Вариант 11.

1. Показать, что для трёх произвольных событий A, B и C соотношение справедливо тогда и только тогда, когдаA∩C = B∩C.

2. На полке лежат 20 фотографий, среди которых 8 фотографий родственников. Наудачу берётся 4 фотографии. Определить вероятность того, что среди них будет хотя бы одна фотография родственников.

3. Известно, что среди 30 лотерейных билетов 10 содержат какой-либо выигрыш. Найти вероятность того, что среди 3 выбранных наудачу билетов: а) один с выигрышем; б) хотя бы один с выигрышем.

4. В квадрат с вершинами (0;0), (0;1), (1;0), (1;1) наудачу брошена точка. Пусть (ξ;η) – её координаты. Определить вероятность P{ξ·η < z}.

5. По каналу связи передаются два сигнала: 0 и 1. Из-за помех сигнал подвергается искажению с вероятностью 0,05 независимо от того, искажались или нет предшествующие сигналы. Зная, что послан двоичный код 11010, найти вероятность того, что: а) код принят без искажения; б) принята комбинация 10001; в) принята комбинация 11111.

6. В порт в течение суток может зайти до 3 пассажирских и до 4 грузовых судов. Вероятности захода пассажирского и грузового судов равны 0,15 и 0,25 соответственно. Какова вероятность захода судна в порт в течение суток? Судно зашло в порт. Что вероятнее: пассажирское ли это судно или грузовое?

7. Вероятность умереть на 71 году жизни равна 0,04. Какова вероятность, что из 3-х лиц 70-ти летнего возраста двое доживут до 71 года?

8. Проверяется партия из 500 изделий на брак. Вероятность того, что изделие бракованное, равна 0,05. Найти с вероятностью 0,940 границы, в которых будет заключено число m бракованных изделий среди проверенных.

9. В практически неограниченной совокупности половина предметов обладает свойством А, а пятая часть – свойством В. Эти свойства распределены между предметами независимо. Произведена случайная выборка 1600 предметов. Какова вероятность того, что в этой выборке частоты свойств А и В уклонятся от вероятности не более, чем на 1%?

Вариант 12.

1. Пусть A Ì B. Упростить выражения: A∩B; AUB; A∩B∩C; AUBUC.

2. В старинной игре в кости необходимо было для выигрыша получить

при бросании трёх игральных костей сумму очков превосходящую 10. Найти вероятности: а) выбросить 11 и 12 очков; б) выигрыша.

3. Девять пассажиров рассаживаются наудачу в трёх вагонах. Найти вероятность, того, что: а) в каждый вагон сядет по три пассажира; б) в один вагон сядут 4, в другой – 3 и в третий – 2 пассажира.

4. В квадрат с вершинами (0;0), (0;1), (1;0), (1;1) наудачу брошена точка. Пусть (ξ;η) – её координаты. Определить вероятность P{½ (ξ + η) < z}.

5. Вероятность поражения стрелком мишени при каждом выстреле равна p. Найти вероятность того, что число последовательных (подряд) промахов будет оставаться меньше трёх в течении а) трёх выстрелов; б) четырёх выстрелов; в) пяти выстрелов.

6. Стрелок А поражает мишень при некоторых условиях стрельбы с вероятностью p₁ = 0,6, стрелок В – с вероятностью p₂ = 0,5 и стрелок С – с вероятностью p₃ = 0,4. Стрелки дали залп по мишени, и две пули попали в цель. Что вероятнее: попал стрелок С в мишень или нет?

7. Сколько изюма должны содержать в среднем сдобные булочки для того, чтобы вероятность иметь хотя бы одну изюминку в булке была не менее 0,99?

8. В некоторой местности в среднем на каждые 100 выращиваемых арбузов приходится один весом не менее 10 кг. Найти вероятность того, что в партии арбузов из этой местности, содержащей 4000 штук, будет а) ровно 3 арбуза весом не менее 10 кг каждый; б) не менее 2 таких арбузов.

9. В водоём выпущено 100 меченых рыб. Вскоре после этого сделали контрольный вылов рыб из этого водоёма: было поймано 400 рыб, среди которых оказалось 5 меченых. Оценить общее количество рыб в этом водоёме с вероятностью а) 0,9; б) 0,6.

Вариант 13.

1. Доказать, что если события A и B независимы, то события A и,и B, итакже независимы.

2. Бросаются две игральные кости. Определить вероятность того, что на верхних гранях появятся следующие числа очков: а) только нечётные; б) сумма которых чётна; в) сумма которых больше, чем их произведение.

3. Слово АПЕЛЬСИН составлено из карточек, на каждой из которых написана одна буква. Затем карточки смешивают и вынимают наугад без возврата по одной. Найти вероятность того, что из вынутых по порядку букв составится слово СПАНИЕЛЬ.

4. В квадрат с вершинами (0;0), (0;1), (1;0), (1;1) наудачу брошена точка. Пусть (ξ;η) – её координаты. Определить вероятность P{|ξ – η| < 1/3}.

5. Вероятность попадания в цель для первого стрелка равна 0,7 , а для второго – 0,8. Стрелки выстрелили одновременно. Какова вероятность того, что лишь один из них попадёт в цель? Какова вероятность того, что первый стрелок попадёт в цель ?

6. На вход радиолокационного устройства с вероятностью p поступает смесь полезного сигнала с помехой, а с вероятностью (1- p) – только одна помеха. В первом случае устройство регистрирует наличие какого-то сигнала с вероятностью p₁, а во втором – с вероятностью p₂. Найти вероятность того, что устройство зарегистрирует наличие какого-то сигнала, и какова при этом вероятность, что в его составе имеется полезный сигнал.

7. (З а д а ч а Б а н а х а) Некий курящий математик носит с собой две коробки спичек. Каждый раз, когда он хочет достать спичку, он выбирает наугад одну из коробок. Найти вероятность того, что когда математик вынет первый раз пустую коробку, в другой коробке окажется r спичек; 1 ≤ r ≤ n, где n – первоначальное число спичек в каждой коробке.

8. Изготовитель отправил торговому предприятию 5000 изделий. Вероятность повреждения каждого изделия в пути равна 0,0002. Какова вероятность того, что предприятие получит не более 3-х повреждённых изделия?

9. Игральную кость бросают 80 раз. Найти приближённо границы, в которых число m выпадений шестёрки будет заключено с вероятностью 0,9973.

Вариант 14.

1. Пусть A, B, C – случайные события. Каков смысл равенств: а) A·B·C = A; б) AUBUC =А.

2. Бросаются три игральные кости. Определить вероятность того, что на верхних гранях появятся следующие числа очков: а) только чётные; б) которые все одинаковы; в) произведение которых делится на их сумму.

3. Монеты общим количеством 20 штук, среди которых 10 – достоинством в 1 руб.; 5 – достоинством в 2 руб.; 3 – достоинством в 5 руб. и остальные номиналом по 10 руб., раскладываются случайным образом на четыре кучки. Какова вероятность того, что в каждой кучке окажутся монеты одного номинала.

4. На отрезок [a;b] длиной l случайным образом бросаются две точки Какова вероятность того, что расстояние между ними не превзойдёт числа λ (0 ≤ λ ≤ l).

5. Имеется группа из k космических объектов, каждый из которых независимо от других обнаруживается радиолокационной станцией с вероятностью p. За группой объектов ведут наблюдения независимо друг от друга m радиолокационных станций. Найти вероятность того, что не все объекты группы будут обнаружены.

6. Предположим, 5% всех мужчин и 25% всех женщин – дальтоники. Какова вероятность того, что наугад выбранное лицо страдают дальтонизмом? Какова вероятность того, что это мужчина ? (Считать, что мужчин и женщин одинаковое число).

7. Вероятность получения удачного результата при проведении сложного эксперимента равна 2/3. Найти наивероятнейшее число удачных опытов, если всего их было проведено 7.

8. Оценить число бракованных изделий в партии из 1000 изделий, если вероятность обнаружить хотя бы одно бракованное среди 10 отобранных для контроля изделий не превосходит 0,1..

9. Вероятность появления успеха в каждом из 625 независимых испытаний равна 0,8. Найти вероятность того, что частота появления успеха отклонится по абсолютной величине от его вероятности не более, чем на 0,04

Вариант 15.

1. Пусть события A и B₁ независимы и независимы также события A и B₂, при этом

B₁∩B₂ = Ø. Доказать, что события A и B₁+B₂ независимы.

2. Бросаются четыре монеты. Определить вероятность того, что : а) только на

одной монете появится герб; б) хотя бы на одной монете появится герб; в) ни на одной монете не появится герб.

3. В лифт семиэтажного дома на первом этаже вошли 3 человека. Каждый из них с одинаковой вероятностью выходит на любом этаже, начиная со второго. Наити вероятности событий: A = {все пассажиры выйдут на седьмом этаже}; B = {все пассажиры выйдут на одном и том же этаже}; C = {все пассажиры выйдут на разных этажах}.

4. Какой толщины должна быть монета, чтобы вероятность события {монета встала на ребро} была бы равна 1/3 ?

5. Два охотника стреляют в волка, причём каждый делает по одному выстрелу. Какова вероятность попадания в волка хотя бы одним из охотников, если вероятность попадания в цель для первого охотника равна 0,8 , а для второго – 0,7? Как изменится результат, если охотники сделают по два выстрела?

6. При помещении в урну тщательно перемешанных n шаров (m белых и n – m чёрных) один шар неизвестного цвета затерялся. Из оставшихся в урне n – 1 шаров наудачу извлекают один. Какова вероятность, что вынутый шар окажется белым? Если так и произошло, то какова вероятность того, что затерялся белый шар?

7. Баскетболист бросает мяч в корзину до первого попадания, но делает не более 6 бросков. Определить вероятность того, что число бросков будет не менее 4.

8. Изделия некоторого производства содержат 2,5% брака. Найти вероятность того, что среди 200 взятых наугад изделий: а) нет ни одного испорченного; б) будет не более одного испорченного.

9. В практически неограниченной совокупности половина предметов обладает свойством А, а пятая часть – свойством В. Эти свойства распределены между предметами независимо. Произведена случайная выборка 1600 предметов. Какова вероятность того, что в этой выборке частоты свойств А и В уклонятся от вероятности не более, чем на 1%?

Вариант 16.

1. Доказать, что если события A и B – независимы с положительными вероятностями,

то они совместны.

2. Бросаются три игральные кости. Определить вероятность того, что на верхних гранях появятся следующие числа очков: а) сумма числа очков не более 16; б) произведение числа очков не менее 16; в) произведение числа очков делится на 16.

3. При наборе телефонного номера абонент забыл две последние цифры и набрал их на удачу, помня только, что эти цифры нечётные и разные. Найти вероятность того, что номер набран правильно

4. В отрезке единичной длины наудачу появляется точка. Определить вероятность того, что расстояние от точки до концов отрезка превосходит величину 1/3.

5. Сколько раз нужно бросить игральную кость, чтобы с вероятностью, не меньшей: а) 0,5; б) 0,9 , хотя бы один раз выпало шесть очков ?

6. Если позволяет погода, лётчик сажает самолёт на аэродром, наблюдая за ним визуально, и вероятность благополучной посадки при этом равна p₁. В условиях низкой облачности лётчик сажает самолёт вслепую по приборам. Надёжность приборов слепой посадки равна P и, если они работали нормально, самолёт садится благополучно с той же вероятностью p₁. Если приборы слепой посадки отказали, то вероятность благополучной посадки самолёта очень мала и равна p*. Найти: а) полную вероятность благополучной посадки самолёта, если в k% всех случаев посадки аэродром затянут низкой облачностью; б) вероятность того, что при благополучном приземлении самолёта лётчик пользовался приборами слепой посадки.

7. На пути движения автомобиля 6 светофоров, каждый из которых может остановить автомобиль с вероятностью 0,8. Определить вероятность того, что автомобиль пройдёт не менее 3-х светофоров до первой остановки.

8. Проверяется партия из 500 изделий на брак. Вероятность того, что изделие бракованное, равна 0,05. Найти с вероятностью 0,940 границы, в которых будет заключено число m бракованных изделий среди проверенных.

9. В водоём выпущено 100 меченых рыб. Вскоре после этого сделали контрольный вылов раб из этого водоёма: было поймано 400 рыб, среди которых оказалось 5 меченых. Оценить общее количество рыб в этом водоёме с вероятностью а) 0,9; б) 0,6.

Вариант 17.

1. Пусть события A, B и С – произвольные случайные события. Выразить через операции с этими событиями события, состоящие в том, что: а) произошло, по крайней мере, два из этих событий; б) произошло два и только два из этих событий; в) произошло не больше двух из этих трёх событий.

2. На шахматную доску из 64 клеток ставятся наудачу две ладьи (чёрная и

белая).

Какова вероятность того, что они не «бьют» друг друга? (В шахматах ладья какого-либо цвета, чёрная или белая, будет иметь под «ударом» ладью противника, т. е. другого цвета, если та стоит на клетках одной горизонтали или одной вертикали с ней).

3. Вероятность того, что цель поражена при одном выстреле первым стрелком, равна p₁ = 0,66, вторым – p₂ = 0,49. первый сделал n₁ = 3, второй – n₂ = 2 выстрела. Определить вероятность того, что цель не поражена.

4. В круг радиуса R вписан квадрат. Какова вероятность того, что поставленные наудачу внутри круга 2 точки окажутся внутри квадрата: а) обе; б) хотя бы одна из них.

5. Прибор состоит из трёх узлов. В первом узле n₁ элементов, во втором n₂ и в третьем n₃. Узел Ι включён последовательно с блоком дублирующих друг друга и потому соединённых параллельно узлов ΙΙ и ΙΙΙ. Надёжность (вероятность безотказной работы) каждого элемента в любом из узлов одинакова и равна p. Выход из строя одного элемента означает выход из строя всего узла. Элементы выходят из строя независимо друг от друга. Найти надёжность прибора P.

6. В группе из 10 студентов, пришедших на экзамен, 3 подготовились отлично, 4 – хорошо, 2 – посредственно и 1 – плохо. В экзаменационных билетах 20 вопросов и отлично подготовленный студент может ответить на все из них, хорошо подготовленный – на 16, посредственно – на 10, плохо – на 5. Какова вероятность, что выбранный наудачу из этой группы студент ответит на три произвольно заданных вопроса? Если это произошло, то найти вероятность того, что студент подготовлен: а) отлично; б) плохо.

7. Вероятность умереть на 71 году жизни равна 0,04. Какова вероятность, что из 3-х лиц 70-ти летнего возраста двое доживут до 71 года?

8. В некоторой местности в среднем на каждые 100 выращиваемых арбузов приходится один весом не менее 10 кг. Найти вероятность того, что в партии арбузов из этой местности, содержащей 4000 штук, будет а) ровно 3 арбуза весом не менее 10 кг каждый; б) не менее 2 таких арбузов.

9. В водоём выпущено 100 меченых рыб. Вскоре после этого сделали контрольный вылов рыб из этого водоёма: было поймано 400 рыб, среди которых оказалось 5 меченых. Оценить общее количество рыб в этом водоёме с вероятностью а) 0,9; б) 0,6.

Вариант 18.

1. Пусть A Ì B. Упростить выражения: A∩B; AUB; A∩B∩C; AUBUC.

2. В старинной игре в кости необходимо было для выигрыша получить, при бросании трёх игральных костей, сумму очков превосходящую 10. Найти вероятности:

а) выбросить 11 и 12 очков; б) выигрыша.

3. Девять пассажиров рассаживаются наудачу в трёх вагонах. Найти вероятность, того, что: а) в каждый вагон сядет по три пассажира; б) в один вагон сядут 4, в другой – 3 и в третий – 2 пассажира.

4. В квадрат с вершинами (0;0), (0;1), (1;0), (1;1) наудачу брошена точка. Пусть (ξ;η) – её координаты. Определить вероятность P{½ (ξ + η) < z}.

5. Вероятность поражения стрелком мишени при каждом выстреле равна p. Найти вероятность того, что число последовательных (подряд) промахов будет оставаться меньше трёх в течении а) трёх выстрелов; б) четырёх выстрелов; в) пяти выстрелов.

6. Стрелок А поражает мишень при некоторых условиях стрельбы с вероятностью p₁ = 0,6, стрелок В – с вероятностью p₂ = 0,5 и стрелок С – с вероятностью p₃ = 0,4. Стрелки дали залп по мишени, и две пули попали в цель. Что вероятнее: попал стрелок С в мишень или нет?

7. Сколько изюма должны содержать в среднем сдобные булочки для того, чтобы вероятность иметь хотя бы одну изюминку в булке была не менее 0,99?

8. В некоторой местности в среднем на каждые 100 выращиваемых арбузов приходится один весом не менее 10 кг. Найти вероятность того, что в партии арбузов из этой местности, содержащей 4000 штук, будет а) ровно 3 арбуза весом не менее 10 кг каждый; б) не менее 2 таких арбузов.

9. Какова вероятность того, что в столбике из 100 наугад отобранных монет будет от 45 до 55 монет, расположенных «гербом» вверх.

Вариант 19.

1. Доказать, что три события 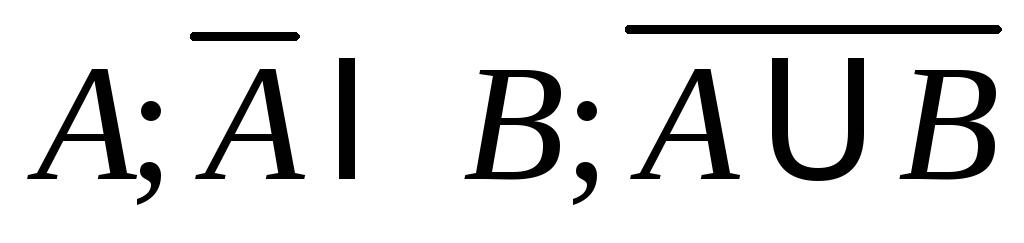образуют полную группу

событий.

2. Из последовательности чисел 1, 2, …, n наудачу выбираются два числа. Какова вероятность того, что одно из них меньше k, а другое больше k, где 1< k < n– произвольное целое число.

3. По линии связи, имеющей 4 приёмнопередающих пункта, передаётся сообщение. На первом пункте происходит искажение сообщения с вероятностью 0,1. На каждом последующем пункте вероятность искажения возрастает на 0,05. Какова вероятность получения неискажённого сигнала?

4. Двое договорились о встрече в определённом месте между двумя и тремя часами дня. Пришедший первым ждёт другого в течении 15 минут, после чего уходит. Чему равна вероятность их встречи, если приход каждого из них в течении указанного часа может произойти в любое время? (Указание: рассматривать моменты прихода лиц как декартовы координаты x и y на плоскости).

5. Студент пришёл на зачёт, зная из 30 вопросов только 24. Какова вероятность сдать зачёт, если после отказа отвечать на вопрос преподаватель задаёт ещё один вопрос?

6. В порт в течении суток может зайти до 3 пассажирских и до 4 грузовых судов. Вероятности захода пассажирского и грузового судов равны 0,15 и 0,25 соответственно. Какова вероятность захода судна в порт в течении суток? Судно зашло в порт. Что вероятнее: пассажирское ли это судно или грузовое?

7. Сколько изюма должны содержать в среднем сдобные булочки для того, чтобы вероятность иметь хотя бы одну изюминку в булке была не менее 0,99?

8. Имеется общество из n = 500 человек. Найти вероятность того, что у двух человек день рождения придётся на Новый год. Вероятность рождения в фиксированный день полагать равной p = 1 / 365.

9. В каждом из n = 600 независимых испытаний событие A происходит с постоянной вероятностью p = 0.85. Найти вероятность того, что относительная частота m/n этого события по модулю от вероятности более чем на: а) ε₁ = 0,0055; б) ε₂ = 0,011.

Вариант 20.

1. Доказать, что

2. В секретном замке на общей оси 4 диска, каждый из которых разделён на 10 секторов, содержащих различные цифры от 0 до 9. Замок открывается лишь в том случае, когда диски установлены так, что цифры на них образуют определённое четырёхзначное число. Найти вероятность того, что при произвольной установке дисков замок откроется.

3. (Преферанс) Колода из 32 карт (от семёрок до тузов) раздаётся на три игрока (по 10 карт каждому) и ещё 2 карты остаётся в прикупе. Один из игроков видит, что у него на руках 6 карт бубновой масти, (что, при взятии игры на себя, позволить объявить эту масть козырной). Беря игру на себя, игрок сбрасывает две из 4-х карт других мастей и берёт две из прикупа. Какова вероятность того, что в прикупе две карты бубновой масти ? Хотя бы одна ?

4. Стержень длины l сломали на три части, выбирая наудачу места разлома. Найти вероятность того, что из получившихся трёх частей можно составить треугольник. (Указание: если x и y – длины двух из этих частей, то для того, чтобы можно было составить треугольник, необходимо выполнение неравенств x, y < l /2; x + y > l /2).

5. По каналу связи передаются два сигнала: 0 и 1. Из-за помех сигнал подвергается искажению с вероятностью 0,05 независимо от того, искажались или нет предшествующие сигналы. Зная, что послан двоичный код 11010, найти вероятность того, что: а) код принят без искажения; б) принята комбинация 10001; в) принята комбинация 11111.

6. Стрелок А поражает мишень при некоторых условиях стрельбы с вероятностью p₁ = 0,6, стрелок В – с вероятностью p₂ = 0,5 и стрелок С – с вероятностью p₃ = 0,4. Стрелки дали залп по мишени, и две пули попали в цель. Что вероятнее: попал стрелок С в мишень или нет?

7. Монета бросается до тех пор, пока герб не выпадет n = 3 раза. Определить вероятность того, что цифра выпадет m = 5 раз

8. На телефонной станции неправильное соединение происходит с вероятностью p = 0,005. Найти вероятность того, что среди n = 200 соединений произойдет: а) одно неправильное; б) менее 3-х неправильных; в) более 2-х неправильных соединений.

9. Производство даёт 1% брака. Какова вероятность того, что из взятых на исследование 1100 изделий выбраковано будет не более 17?

Вариант 21.

1. Пусть события A, B и С – произвольные случайные события. Выразить

через операции с этими событиями события, состоящие в том, что: а) произошло, по крайней мере, одно из этих событий; б) произошло одно и только одно из этих событий; в) произошло только A.

2. На пяти карточках написаны цифры: 1, 2, 3, 4, 5. Вынимается одна карточка и записывается стоящее на ней число, после чего карточка кладётся обратно и смешивается с остальными. Затем вынимается вторая карточка и число, стоящее на ней, сравнивается с ранее записанным числом. Определить вероятности следующих событий: A – второе число больше первого; B – оба числа одинаковы; C – второе число меньше первого.

3. Девять пассажиров рассаживаются наудачу в трёх вагонах. Найти вероятность, того, что: а) в каждый вагон сядет по три пассажира; б) в один вагон сядут 4, в другой – 3 и в третий – 2 пассажира.

4. В квадрат с вершинами (0;0), (0;1), (1;0), (1;1) наудачу брошена точка. Пусть (ξ; η) – её координаты. Определить вероятность P{ξ·η < z}.

5. Вероятность поражения стрелком мишени при каждом выстреле равна p. Найти вероятность того, что число последовательных (подряд) промахов будет оставаться меньше трёх в течении а) трёх выстрелов; б) четырёх выстрелов; в) пяти выстрелов.

6. В одной урне 5 белых и 6 чёрных шаров, а в другой – 4 белых и 8 чёрных шаров. Из первой урны случайным образом вынимают 3 шара и опускают во вторую урну. После этого из второй урны также случайно извлекают 4 шара. Найти вероятность того, что все шары, вынутые из второй урны – белые. Оценить, при таком исходе, вероятность того, что на первом этапе из первой урны извлекли 3 чёрных шара.

7. Вероятность выигрыша по лотерейному билету равно p = 0,3. Куплено n = 13 билетов. Найти наивероятнейшее число выигравших билетов и соответствующую вероятность.

8. На телефонной станции неправильное соединение происходит с вероятностью p = 0,004. Найти вероятность того, что среди n = 100 соединений произойдет: а) два неправильное; б) менее 4-х неправильных; в) более 3-х неправильных соединений.

9. Всхожесть семян данного растения равна 0,9. Найти вероятность того, что из 900 посаженных семян число проросших будет заключено между 790 и 890.

Вариант 22.

1. Последовательно бросают три монеты. Рассмотрим события A = {выпадение «герба» на первой монете}и B = {выпадение хотя бы одной «решётки»}. Определить, зависимы ли эти события и, если зависимы, то как?

2. На 10 карточках написаны цифры от 0 до 9. Карточки перевёрнуты и тщательно перемешаны. Две из них извлекаются наугад и укладываются на стол в порядке появления, затем читается полученное двухзначное число. Найти вероятность, что число будет: а) чётным; б) делится на 4. Как изменятся эти вероятности, если из карточек выкладывать трёхзначное число?

3. Известно, что среди 30 лотерейных билетов, 10 содержат какой-либо выигрыш. Найти вероятность того, что среди 3 выбранных наудачу билетов: а) один с выигрышем; б) хотя бы один с выигрышем.

4. В квадрат с вершинами (0;0), (0;1), (1;0), (1;1) наудачу брошена точка. Пусть (ξ; η) – её координаты. Определить вероятность P{½ (ξ + η) < z}.

5. В двух партиях k₁ = 71% и k₂ = 47% доброкачественных изделий соответственно. Наудачу выбирают по одному изделию из каждой партии. Какова вероятность обнаружить среди них: а) хотя бы одно бракованное; б) два бракованных; в) одно доброкачественное и одно бракованное.

6. Имеется три партии микросхем общей численностью n = 1000 штук, причем n₁ = 160 и n₂ = 570 в первой и второй партиях. В первой партии 6%, во второй – 5%, а в третьей – 4% бракованных изделий. Наудачу из общего количества выбирается одна микросхема. Какова вероятность, что она – бракованная? Какова вероятность, что эта микросхема принадлежит третьей партии изделий?

7. Наблюдениями установлено, что в некоторой местности в сентябре в среднем бывает 12 дождливых дней. Какова вероятность, что из случайно выбранных в этом месяце 8 дней 3 дня окажутся дождливыми?

8. Средняя плотность болезнетворных микробов в одном кубическом сантиметре воздуха равна 100. Берётся на пробу 2 дм³ воздуха. Найти вероятность того, что в нём будет обнаружен хотя бы один микроб.

9. Сколько нужно произвести опытов с бросанием монеты, чтобы с вероятностью 0,92 можно было ожидать отклонение частоты выпадения «герба» от теоретической вероятности 0,5 на абсолютную величину меньшую, чем 0,01?

Вариант 23.

1. Пусть события A, B и С – произвольные случайные события. Каков смысл равенств: A∩B∩С = BUС и AUBUС = A и возможно ли их одновременное выполнение?

2. На полке лежат 20 фотографий, среди которых 8 фотографий родственников. Наудачу берётся 4 фотографии. Определить вероятность того, что среди них будет хотя бы одна фотография родственников.

3. Девять пассажиров рассаживаются наудачу в трёх вагонах. Найти вероятность, того, что: а) в каждый вагон сядет по три пассажира; б) в один вагон сядут 4, в другой – 3 и в третий – 2 пассажира.

4. В квадрат с вершинами (0;0), (0;1), (1;0), (1;1) наудачу брошена точка. Пусть (ξ; η) – её координаты. Найти вероятность того, что корни уравнения x² + ξ·x + η = 0 – действи-тельные.

5. В урне 6 белых и 5 чёрных шаров. Из урны случайно извлекают 4 шара. Найти вероятность того, что среди них имеются: а) 2 белых шара; б) меньше двух белых шаров; в) хотя бы один белый шар.

6. В трёх урнах содержатся шары: в первой – 2 белых и 3 чёрных; во второй – 2 белых и 2 чёрных; в третьей – 3 белых и 1 чёрный шар. Из первой урны наугад переложен шар во вторую. После этого также перекладывают шар из второй урны в третью и, наконец, перекладывают шар из третьей урны в первую. Какой состав шаров в первой урне после этого наиболее вероятен? Определить вероятность того, что состав шаров во всех урнах останется без изменений.

7. Что вероятнее, выиграть у равносильного противника: 1) три партии из четырёх или пять из восьми? 2) не менее трёх партий из четырёх или не менее пяти партий из восьми?

8. В некоторой местности в среднем на каждые 100 выращиваемых арбузов приходится один весом не менее 10 кг. Найти вероятность того, что в партии арбузов из этой местности, содержащей 4000 штук, будет а) ровно 3 арбуза весом не менее 10 кг каждый; б) не менее 2 таких арбузов.

9. В первые классы школы принимают 200 детей. Определить вероятность того, что среди них окажется 100 девочек, если вероятность рождения мальчика равна 0,515.

Вариант 24.

1. Показать, что для трёх произвольных событий A, B и C соотношение справедливо тогда и только тогда, когдаA∩C = = B∩C.

2. В старинной игре в кости необходимо было для выигрыша получить при бросании трёх игральных костей сумму очков превосходящую 10. Найти вероятности: а) выбросить 11 и 12 очков; б) выигрыша.

3. Слово ВЕРОЯТНОСТЬ составлено из карточек, на каждой из которых написана одна буква. Затем карточки смешивают и вынимают наугад без возврата по одной. Найти вероятность того, что из вынутых по порядку букв составится первоначальное слово.

4. В квадрат с вершинами (0;0), (0;1), (1;0), (1;1) наудачу брошена точка. Пусть (ξ; η) – её координаты. Найти вероятность того, что ξ + η ≤ 1.

5. Сколько раз надо бросить пару игральных костей, чтобы с вероятностью не менее 0,5 хотя бы однажды выпало одинаковое число очко на костях?

6. Три орудия производят стрельбу по трём целям. Каждое орудие выбирает себе цель случайным образом и независимо от других. Цель, обстрелянная одним орудием, поражается с вероятностью p. Определить вероятность того, что из трёх целей будут поражены только две. Если такое произошло, как изменится оценка вероятности того, что были обстреляны все три цели (оценить эту величину в общем случае и при p = 0,6)?

7. При въезде в новую квартиру в осветительную сеть было включено 2k новых электролампочек. Каждая из них в течение года перегорает с вероятностью p. Найти вероятность того, что в течение года не менее половины первоначально включенных лампочек придётся заменить новыми. Оценить эту вероятность в общем случае и найти её значение при k = 9 и p = 0,1.

8. Прядильщица обслуживает 1000 веретён. Вероятность обрыва нити на одном веретене в течение одной минуты равна 0,004. Найти вероятность того, что в течение одной минуты обрыв произойдет: а) хотя бы на одном веретене; б) на двух веретёнах.

9. Вероятность рождения мальчика равна 0,515 , а девочки 0,485. В некоторой семье шестеро детей. Найти вероятность того, что среди них не больше двух девочек.

Вариант 25.

1. Пусть A Ì B. Упростить выражения: A∩B; AUB; A∩B∩C; AUBUC.

2. Бросаются две игральные кости. Определить вероятность того, что: а) сумма числа очков не превосходит N = 8; б) произведение числа очков не превосходит N = 16; в) произведение числа очков делится на N = 4.

3. Имеются изделия четырёх сортов, причём число изделий i -го сорта (i = 1, 2, 3, 4) равно n_i (n₁ = 2; n₂ = 3; n₃ = 4: n₄ = 2 соответственно). Определить вероятность, что среди них m₁ = 1 первосортных, m₂ = 2, m₃ = 3 и m₄ = 1 второго, третьего и четвёртого сорта соответственно (m₁ + m₂ + m₃ + m₄ = m).

4. В квадрат с вершинами (0;0), (0;1), (1;0), (1;1) наудачу брошена точка. Пусть (ξ;η) – её координаты. Доказать, что для 0 ≤ x; y ≤ 1 P{ξ < x; η < y}=P{ξ < x}· P{η < y}= xy.

5. Сколько раз надо бросить пару игральных костей, чтобы с вероятностью не менее 0,9 хотя бы однажды на костях выпало 8 очков?

6. В пирамиде стоят без определённого порядка 18 винтовок, 3 из которых с оптическим прицелом. Стрелок, стреляя из винтовки с оптическим прицелом, поражает мишень с вероятностью 0,9 , а стреляя из винтовки без оптического прицела – с вероятностью 0,75. Какова вероятность того, что стрелок поразит мишень стреляя из случайно взятой винтовки? Если мишень поражена, то какова вероятность того, что это сделано из винтовки с оптическим прицелом.

7. Изделия некоторого производства содержат 5% брака. Найти вероятность того, что среди десяти взятых наугад изделий: а) нет ни одного испорченного; б) будут два испорченных; в) будет менее трёх испорченных.

8. В опытах Резерфорда с α – излучением радиоактивное вещество испускало в среднем 3,87 α-частиц за 7,5 секунд. Найти вероятность того, что за 1 с это вещество испустит хотя бы одну α-частицу.

9. Вероятность появления положительного результата в каждом из n испытаний равна 0,9. Сколько нужно произвести опытов, чтобы с вероятностью не меньшей 0,98 можно было ожидать, что не менее 150 опытов дадут положительный результат?