6.2. Оптимальная фильтрация случайного сигнала
Более сложной и общей, чем задача оценивания постоянного параметра, является задача оценивания изменяющегося сообщения (первичного сигнала) на основе наблюдаемой реализации. Такое оценивание принято называть фильтрацией.
Сообщение рассматривается как реализация случайного процесса, множество всевозможных сообщений – как ансамбль реализаций с некоторым вероятностным распределением. Сообщение (первичный сигнал) модулирует несущее колебание, поэтому сигнал на выходе канала связи также случаен. Таким образом, ставится задача по наблюдаемому случайному колебанию оценить другое случайное колебание (первичный сигнал, или закон модуляции), связанное с наблюдаемым в общем случае нелинейным образом (задача нелинейной фильтрации, или демодуляции). Эта задача может быть весьма сложной.
В этом подразделе рассматривается наиболее простой случай оптимальной линейной фильтрации.
Пусть сигнал на входе линейного фильтра представляет собой сумму переданного сигнала S(t) и помехи ξ(t)
x(t) = S(t) + ξ(t)
Требуется найти такую передаточную характеристику K(ω), которая минимизирует средний квадрат погрешности
2 (t ) S (t ) S (t ) 2 |
(6.8.) |
где S(t) – оценка сигнала на выходе фильтра. Здесь, считаем, что время запаздывания сигнала S(t) в фильтре τz = 0, а среднее значение берется по
ансамблям сигналов S(t) и помех ξ(t). Считаем также, что S(t) и ξ(t) стационарные взаимно-некоррелированные процессы с известными спектрами плотности мощности Gs(ω) и Gξ(ω). Для отклика сигнала на
выходе фильтра запишем
y(t) = L[S(t) + ξ(t)] где L[-] – оператор линейного преобразования.
Среднеквадратическую погрешность (6.8) можно представить двумя |
|
составляющими |
2 (t) S2 (t) 2 (t) |
где |
составляющая, обусловленная искажениями |
сигнала в фильтре (считаем ФЧХ линейной, т.е.φ(ω) = -ω τz); |
|
2 ( t ) L ( t ) 2 |
– составляющая, обусловленная действием шума. |
Принимая во внимание, что |
|
|
|
|
|
|
1 |
|
|
( )1 |
|
|
|
j z |
e |
j t |
|
||||||||
|
|
|
|
|
|
|
S |
(t) |
|
|
|
S |
K( )e |
|
|
d |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
для спектральной плотности мощности |
G S ( ) имеем |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
S |
|
|
|
S |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||
|
|
G |
|
( ) G |
|
( ) 1 |
K( ) |
|
|
|
|
|
|
||||||||||||
В свою очередь, спектральная плотность мощности составляющей |
|||||||||||||||||||||||||
шума равна |
G |
( ) G ( )K 2 ( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
а для Gε(ω) суммарной погрешности получим |
|
|
G ( )K |
|
( ) |
|
|
|
|||||||||||||||||
G ( ) G S ( ) G |
( ) GS ( ) 1 K( ) |
2 |
2 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.9) |
|
||||
Найдем теперь выражение K(ω) – при котором суммарная |
|||||||||||||||||||||||||
погрешность становится минимальной: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
dG ( ) |
2G |
( ) 1 K( ) |
2G K( ) 0 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
dK( ) |
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
откуда |
|
|
|
|
|
|
GS ( ) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Kоф ( ) |
|
|
|
|
|
(6.10) |
|
|
|
|
|
||||||||||
|
|
|
|
|
GS |
( ) G ( ) |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
или |
|
|
|
|
|
|
|
|
|
GS ( ) |
|
|
|
e |
j z |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Kоф ( ) |
GS ( ) G ( ) |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.11) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Фильтр (6.11), обеспечивающий минимальную среднеквадратичную погрешность случайного сигнала на фоне белого шума называется оптимальным фильтром Колмогорова-Винера. Следует отметить, что фильтр Колмогорова-Винера с коэффициентом передачи (6.11) физически не реализуем.
Конструктивные результаты в решении задачи синтеза фильтра, оптимального по критерию минимума СКП получил Рудольф Эмиль Калман, который в качестве априорных данных о сообщении использовал рекуррентную модель: состояние - наблюдение. Предполагается, что сообщение a(t) порождается линейным стохастическим дифференциальным уравнением состояния
|
da |
a(t) n1 (t) |
, |
(6.12) |
dt |
|
|
|
|
|
где n1(t) – нормальный белый шум (порождающий процесс). Физически
это означает, что сообщение a(t) моделируется как результат прохождения белого шума через интегрирующую цепь с постоянной времени α = 1/RС.
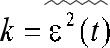
Рассмотрим случай линейной фильтрации, когда наблюдаемый процесс на входе фильтра задан уравнением наблюдения
x(t) = S(t, a(t)) + ξ(t) = a(t) f(t) + ξ(t),
где сообщение a(t) – задано уравнением (6.12); S(t, a(t)) – сигнал; f(t) – носитель; ξ(t) – белый гауссовский шум.
Принимая во внимание основное условие линейной оптимальной |
|
|
(t) должна быть |
фильтрации, состоящее в том, чтоб ошибка (t) S(t) S |
|
не коррелированна со входным сигналом x(t), рекурентное соотношение,
имеет вид: |
da |
|
|
2k |
|
|
|
|
||
(6.13) |
dt |
a(t) |
G0 |
f (t) |
x(t) a(t) f (t) |
|
||||
dk |
|
N1 |
|
|
2 |
|
|
|||
|
|
|
2 k |
f 2 k 2 |
|
|||||
|
|
|
|
|||||||
|
|
dt |
|
|
|
|||||
|
|
2 |
|
|
|
N0 |
|
|||
(6.14) |
|
|
|
|
|
|
|
|
|
|
Уравнения (6.13) и (6.14) принято называть уравнениями фильтра Калмана. Уравнение (6.13) определяет алгоритм формирования оценки, а следовательно, и структурную схему фильтра, а (6.14) – ошибку фильтрации .
Структурная схема, моделирующая уравнение (6.13) приведена на рис. 6.4. Этот фильтр представляет собой динамическую систему с переменным коэффициентом усиления, величина которого зависит от точности текущих оценок (дисперсии погрешности фильтрации) и уровня шумов наблюдения. Иначе говоря, фильтр Калмана можно рассматривать как линейную следящую систему, эффективная полоса пропускания которой, изменяется в процессе работы.
Рис. 6.4.
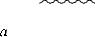
6.3. Потенциальной помехоустойчивости передачи непрерывных сообщений
Пусть передается непрерывное сообщение a(t), причём |a(t)| ≤ 1, а его
мощность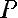 
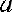
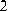
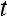
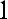; в общем случае a(t) можно представить в виде
n
разложения a(t) i i (t) по единичным ортогональным составляющим с коэффициентами i. Тогда сигнал S(t; a) = S(t; λ1, λ2, …λn) будет получать
в процессе |
модуляции приращения в соответствии с модуляционным |
||
|
Di |
dS(t) |
|
вектором |
d |
определяющим свойства модулятора. |
|
|
|
i |
|
С другой стороны, принятый сигнал S*(t) за счет действующей в канале помехи ξ(t) будет отличаться от переданного S(t). Как следствие этого, коэффициенты λi = λi + λi также будут отличаться от переданных λi.
В результате будем иметь
|
|
|
) i (t) |
a |
(t) i i (t) ( i i |
||
|
|
|
(6.15) |
a(t) i i (t)
а для погрешности передачи получим (t) a (t) a(t) i i (t).
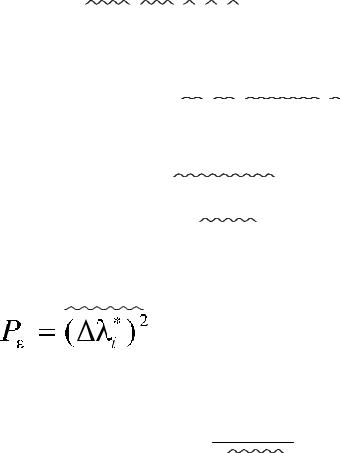
Оптимальный приемник Котельникова измеряет расстояние
R S ( t ) S ( t ) 2 .
Минимальному |
значению |
R соответствуют приращения λi*, |
|||||
определяемые из условия |
d |
|
|
|
|
d |
|
dR |
|
|
|
(t) S(t) |
dS |
0 |
|
|
|
2 S |
|
||||
|
i |
|
|
|
|
i |
|
|
|
|
|
(t ) Di (t ) |
|
|
|
т.е. |
i |
Di2 (t ) |
|
|
|||
|
|
|
|
|
|||
(6.16) |
|
|
|
|
|
|
|
На основе (6.16) получаем выражение для средней мощности шума на |
|||||||
выходе приемника |
|
|
|
. |
Кроме того, при слабых помехах ξ(t) |
||
|
|
|
|
|
G ( ) |
|
|
можно считать, что спектральную мощность шума на выходе можно |
|||||||
представить в виде |
G ( |
) |
|
|
|||
(6.17) |
|
|
|
|
D i2 ( t ) |
|
, |
|
|
|
b |
|
|
||
а Pε – соответственно |
|
P |
G ( )d |
|
|||
|
|
|
|
0 |
|
|
|
(6.18)
Составим отношение средних мощностей сообщения и шума на выходе |
||||||
приемника |
h2 Pa |
|
|
1 |
(6.19) |
|
|
2 |
P |
|
|
|
|
|
|
|
b |
|
|
|
G( )d
0
Выражения (6.18) и (6.19) используются для сравнительной оценки потенциальной помехоустойчивости различных видов модуляции. В результате анализа получены следующие выражения Gε(ω) и h22.
Амплитудная модуляция |
S(t) A 1 ma(t) |
cos |
t |
|
|
|
||||||||||||||||||
2G0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|||||||
G ( ) |
|
h;2 |
|
|
m2 A2 |
|
|
|
|
|
|
|
|
|||||||||||
2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
(6.20) |
|
|
|
m A |
|
|
|
2 |
|
|
2G0 b |
|
|
|
|
|
|
|||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
t |
m |
a(t) |
|
|
|
|
|
|
|
||||||||
Фазовая модуляция |
S(t) Acos |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2G0 |
|
|
|
|
|
|
2 A2 |
|
|
|
|
|
|
|
|
||||||
G ( ) |
|
|
|
|
|
|
h |
2 |
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
||
m2 A2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2G0 b |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
2; |
|
|
|
|
|
|
|
|
|
||||||||||
(6.21) |
S(t) Acos t |
|
t |
a(t)dt |
|
; a(t) cos t ; |
m |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2G |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 2 A2 |
|
|
|
|
||||||
Частотная модуляция |
|
|
|
|
0 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 2G0 b |
|
|
|
||||||||||||
G ( ) m2 A2 |
|
h2 |
|
|
|
|||||||||||||||||||
;
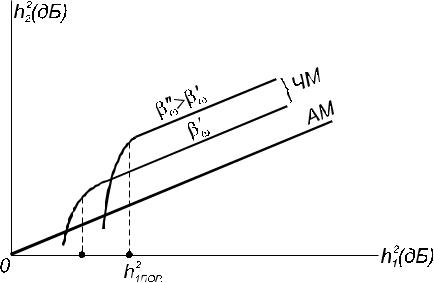
Из (6.20-6.22) следует, что при АМ (m = 1) помехоустойчивость можно |
увеличить лишь за счет увеличения мощности сигнала; при ФМ и ЧМ |
помехоустойчивость можно увеличить также путем увеличения индексов |
модуляции φm и , что достигается за счет расширения спектра сигнала. |
Все широкополосные системы модуляции обеспечивают высокую |
помехоустойчивость h22 при условии, что отношение сигнал-помеха на |
входе h12 больше некоторого порогового значения (рис. 6.5). При h12 < h12пор |
широкополосные системы теряют свои преимущества (резко снижается |
помехоустойчивость); возникающее при этом явление называют явлением |
порога помехоустойчивости. |
Рис. 6.5. Графики Gε(ω) для АМ, ФМ и ЧМ в соответствии с 6.20-6.22 |