Построим сечение вращающегося тела на рис. 7 плоскостью, перпендикулярной оси вращения, рис. 8
Рассмотрим какую-нибудь точку М вращающе- гося тела, находящуюся на расстоянии R от оси вращения, рис. 8.
Рис. 7
Рис. 8
Положение точки M на траектории |
определяется дуговой |
|
координатой s, начало которой совпадает с |
плоскостью P. |
31 |
Угол между плоскостью Q и радиусом R при вращении тела остаётся постоянным ( =const).
Дуговая координата точки M равна:
s R .
Проекция скорости точки на касатель- ную к траектории точки равна
v |
ds |
R |
d |
|
d |
|
0 |
|
R . |
|
|
|
|
|
|||||||
dt |
dt |
dt |
R |
|
|
|||||
|
|
|
|
|
|
|
|
|||
Таким образом, скорость точки вращающегося тела равна произведению его угловой скорости на расстояние от этой точки до оси вращения и направ- лена перпендикулярно радиусу её траектории,
рис. 8.
v R .
Рис. 8
(18)
Из (18) следует, что скорости точек вращающегося тела |
|
пропорциональна их расстояниям до оси вращения. |
32 |
Характер распределения скоростей точек вращающегося тела, лежащих на линии, проходящей через ось вращения приведен на рис. 9.
Рис. 9
Чтобы найти ускорение точки M воспользуемся формулами для определения ускорения точки при естественном способе задания
её движения. |
dv |
|
v2 |
|
|
|
a |
, an |
. |
(19) |
|||
dt |
R |
|||||
|
|
|
|
Подставляя сюда скорость точки из (15), получим:
a |
|
dv |
|
d R |
Rd R , a |
n |
|
v2 |
|
R 2 |
R 2. |
|
|
|
|||||||||
|
dt |
|
dt |
dt |
|
R |
|
R |
33 |
||
|
|
|
|
|
|
|
Таким образом, касательные и нормальные ускорения точек вращающегося тела пропорциональны их расстояниям до оси
вращения. |
a R , |
an R 2. |
(20) |
|
Касательное ускорение направлено по касательной к траектории точки (в сторону вращения, если тело вращается ускоренно, или в обратную сторону, если вращение замедленное); нормальное ускорение всегда направлено по радиусу R к оси вращения, рис. 10.
Рис. 10 |
34 |
Полное ускорение точки M равно: |
|
|
|
|
a a2 an2 |
R 2 R 2 |
2 R |
2 4 . |
(21) |
Угол отклонения полного ускорения точки M от радиуса траектории определяется по формуле:
tan a . an
Подставляя сюда касательное и нормальное ускорения из (19), получим:
tan |
|
a |
|
|
|
R |
|
|
tan |
|
|
|
|
|
. |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
an |
|
2 |
|
|
2 |
|||||||||
|
|
|
|
R |
|
|
|||||||||
Характер распределения ускорений точек вращающегося тела приведен на рис. 11.
Рис. 10 35
9. Векторные выражения скорости и ускорений точки вращающегося тела
Функцию угла вращения тела можно изобразить в виде вектора направленного, вдоль оси вращения в ту сторону, откуда видим,
что тело вращается против хода часовой стрелки.
d r dt .
Дифференцируя вектор по времени, получим вектор угловой
скорости, также направленный вдоль оси вращения.
36
Производная по времени от вектора угловой скорости равна вектору углового ускорения, который тоже направлен вдоль оси вращения.
d r. dt
При этом, если вращение тела ускорен- ное, то направления векторов угловой скорости и углового ускорения совпадают. В противном случае направления векто- ров угловой скорости и углового уско- рения противоположны, рис. 11.
Рис. 11
37
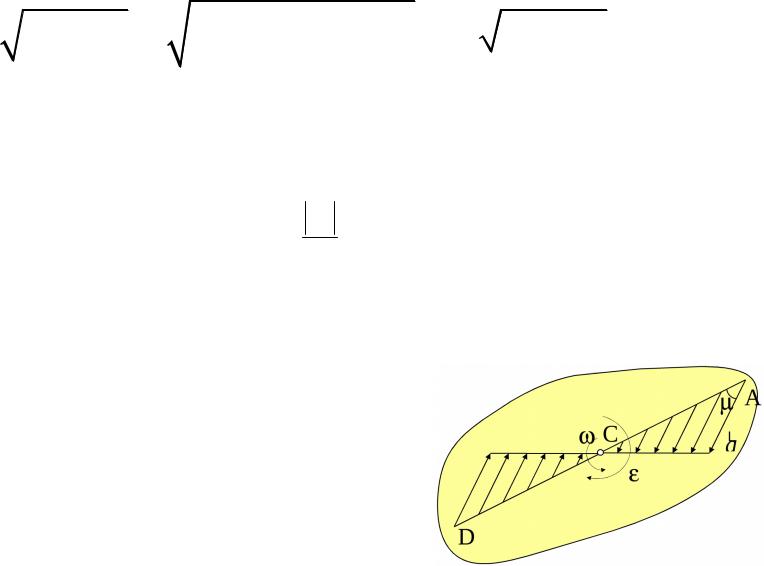
Приведем векторные выражения скорости и ускорения точки вращающегося тела.
Пусть тело совершает вращательное движение и в данный момент времени известны характеристики его движения и , рис. 12.
Из произвольной точки О оси вращения проведем радиус-вектор точки М (причем угол MСO = 90° и MС = R = r sin ).
Найдём модуль векторного произведения
|
|
|
|
|
|
|
|
r. |
|
||||
|
r |
|
|
|
|
|
r sin |
|
|
|
R v. |
|
|
|
|
|
|
|
|
|
|||||||
Как видим, модуль векторного |
|
||||||||||||
произведения r |
равен скорости точки. |
Рис. 12 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
38 |
Направление векторного произведения определяется по правилу векторного произведения.
Результат векторного произведения равен третьему вектору, построенному в точке приложения перемножаемых векто-ров перпендикулярно плоскости, проведён-ной через эти векторы и направленному в ту сторону, откуда видно, что кратчайший поворот от первого умножаемого вектора ко
второму осуществляется против хода Рис. 12 часовой стрелки.
Как видим, по направлению векторное произведение r совпадает с направлением скорости точки М.
39
Таким образом, векторного произведения r по величине и направлению это векторное произведение совпадает с вектором скорости. Следовательно, вектор скорости любой точки вращающегося тела равен векторному произведению угловой скорости тела на радиус-вектор этой точки (формула Эйлера):
v r. |
(22) |
Вектор ускорения точки М определим как производную вектора скорости по времени:
r |
|
dv |
|
d |
r |
r |
d |
r |
|
a |
|
|
|
|
r |
|
r |
||
dt |
dt |
||||||||
|
|
|
|
|
dt |
|
|||
|
r |
dr |
|
|
|
|
|
dt |
|
|
Или
a r v . |
(23) |
40