
- •Раздел 1. Алгебраические структуры Тема 1.1. Бинарные операции и их свойства
- •Тема 1.2. Алгебраические структуры
- •Тема 1.3. Основные свойства групп
- •Тема 1.4. Поля и кольца
- •Раздел 2. Алгебра множеств Тема 2.1. Основные определения теории множеств
- •Тема 2.2. Подмножество, понятие универсального множества
- •Тема 2.3. Операции над множествами
- •Раздел 3. Основные теоремы комбинаторики
- •Тема 3.1. Метод математической индукции
- •Тема 3.2. Основные принципы комбинаторики
- •Раздел 4. Комбинаторные объекты Тема 4.1. Сочетания
- •Тема 4.2. Размещения и перестановки
- •Раздел 5. Полиномиальные тождества Тема 5.1. Бином Ньютона
- •Тема 5.2. Понятие о методе рекуррентных соотношений
- •Тема 5.3. Метод производящих функций
- •Тема 5.4. Метод траекторий
- •Тема 5.5. Примеры комбинаторных задач
- •Раздел 6. Соответствие, отношение, отображение Тема 6.1. Понятие кортежа. Декартово произведение множеств
- •Тема 6.2. Определения и свойства
- •Тема 6.3. Типы отношений
- •Пересечение и объединение отношений
- •Композиция отображений и отношений
- •Тема 6.5. Решётки
- •Тема 6.4. Верхняя и нижняя границы множества.
- •Раздел 7. Операции булевой алгебры Тема 7.1.Понятие высказывания, простые и составные высказывания
- •Тема 7.2.Операции на множестве высказываний
- •Отрицание
- •Конъюнкция
- •Дизъюнкция
- •«Исключающее или»
- •Импликация
- •Эквивалентность
- •Штрих Шеффера
- •Раздел 8. Законы и тождества Булевой алгебры Тема 8.1.Формулы Булевой алгебры
- •Тема 8.2.Законы и тождества Булевой алгебры
- •Тема 8.3.Составление формулы по заданной таблице истинности
- •Тема 8.4. Двойственность
- •Тема 8.5.Булева алгебра и теория множеств
- •Тема 8.6.Днф, интервалы и покрытия
- •Раздел 9. Функциональная полнота. Алгебра Жегалкина
- •Тема 9.1.Функционально полные системы
- •Тема 9.2.Алгебра Жегалкина и линейные функции
- •Тема 9.3.Замкнутые классы. Монотонные функции
- •Тема 9.4.Теоремы о функциональной полноте
- •Раздел 10. Хорновские формулы
- •Тема 10.1.Задача получения продукции
- •Тема 10.2.Решение задачи о продукции
- •Алгоритм замыкание(X,f)
- •Алгоритм ПрямаяВолна(X,y,f)
- •Алгоритм БыстроеЗамыкание(X,f)
- •Раздел 11. Теория релейно-контактных схем Тема 11.1.Основные понятия
- •Тема 11.2.Основные задачи теории релейно-контактных схем
- •Тема 11.3.Построение машины голосования
- •Тема 11.4.Двоичный сумматор
- •Тема 11.5.Методы упрощения логических выражений. Методы решения логических задач
- •Раздел 12. Логика предикатов Тема 12.1.Определение предиката
- •Тема 12.2.Логические операции над предикатами
- •Тема 12.3.Кванторы
- •Тема 12.4. Истинные формулы и эквивалентные соотношения
- •Тема 12.5.Доказательства в логике предикатов
- •Раздел 13. Теория графов
- •Тема 13.1.Основные определения теории графов
- •Тема 13.2. Способы задания графов
- •Тема 13.3. Отношения порядка и эквивалентности на графе
- •Тема 13.4. Числовые характеристики графа
- •Тема 13.5.Изоморфизм графов
- •Раздел 14. Проблемы достижимости на графах Тема 14.1.Граф достижимости
- •Тема 14.2.Взаимная достижимость, компоненты сильной связности и базы графа
- •Раздел 15. Некоторые классы графов Тема 15.1.Деревья
- •Тема 15.2. Обход графа
- •Тема 15.3. Расстояния. Диаметр, радиус и центр графа. Протяжённости.
- •Раздел 16. Машина Тьюринга
- •Тема 16.1. Формальное описание машины Тьюринга
- •Тема 16.2. Примеры построения машины Тьюринга
- •Тема 16.3. Свойства машины Тьюринга как алгоритма
- •Раздел 17. Машина Поста
- •Тема 17.1. Теоретическая часть. Состав машины Поста
- •Тема 17.2. Применимость программ. Определение результата выполнения программ
- •Раздел 18. Основные понятия теории автоматов Тема 18.1. Общие подходы к описанию устройств, предназначенных для обработки дискретной информации
- •Тема 18.2. Способы задания конечного автомата
- •Тема 18.3. Эквивалентные автоматы
- •Тема 18.4. Автоматы Мура и Мили
- •Тема 18.5. Примеры синтеза автоматов
Тема 18.3. Эквивалентные автоматы
Автоматы
являются устройствами для переработки
дискретной информации. При этом характером
перерабатываемой информации определяется
входной и выходной алфавиты (![]() и
и![]() );
алфавит внутренних состояний (
);
алфавит внутренних состояний (![]() )
определяется строением автомата и,
вообще говоря, он может различаться у
разных автоматов с одинаковыми входными
и выходными алфавитами. Следовательно,
одно и то же преобразование информации
может быть осуществлено автоматами с
разным числом состояний и, следовательно,
посредством различного числа команд.
Введём ряд определений:
)
определяется строением автомата и,
вообще говоря, он может различаться у
разных автоматов с одинаковыми входными
и выходными алфавитами. Следовательно,
одно и то же преобразование информации
может быть осуществлено автоматами с
разным числом состояний и, следовательно,
посредством различного числа команд.
Введём ряд определений:
Состояния
![]() автомата
автомата![]() и
и![]() автомата
автомата![]() считаются эквивалентными, если оба
автомата, получив одну и ту же (любую)
входную последовательность символов,
перерабатывают её в одинаковую выходную
последовательность.
считаются эквивалентными, если оба
автомата, получив одну и ту же (любую)
входную последовательность символов,
перерабатывают её в одинаковую выходную
последовательность.
Автоматы
![]() и
и![]() называются эквивалентными, если для
каждого состояния автомата
называются эквивалентными, если для
каждого состояния автомата![]() существует эквивалентное ему состояние
автомата
существует эквивалентное ему состояние
автомата![]() и наоборот.
и наоборот.
Другими словами, эквивалентные автоматы реализуют одинаковые преобразования, но могут иметь различное число внутренних состояний.
Понятие
эквивалентности состояний применимо
и к одному автомату (формально можно
считать, что
![]() и
и![]() совпадают). Для одного автомата
эквивалентными будут различные состояния,
через которые одна и та же входная
последовательность символов преобразуется
в одинаковую выходную.
совпадают). Для одного автомата
эквивалентными будут различные состояния,
через которые одна и та же входная
последовательность символов преобразуется
в одинаковую выходную.
Тема 18.4. Автоматы Мура и Мили
На практике наибольшее распространение получили два класса автоматов - автоматы Мили и Мура. Закон функционирования автомата Мили задаётся уравнениями:

Автоматами Мура называют автоматы, у которых выход зависит только от состояния, и не зависит от значения входа:

Теорема: Для любого автомата Мура существует эквивалентный автомат Мили и наоборот.
Доказательство теоремы построим на преобразовании автомата одного типа в автомат другого типа, на примере конкретных автоматов, описанных с помощью графов.
Необходимость: Докажем, что для любого (полностью определённого) автомата Мура существует эквивалентный ему автомат Мили.
Рассмотрим автомат Мура, описанный в виде графа
![]()
![]()
![]()

Перенесём выходы автомата с вершин графа на входящие ветви графа.


![]()
![]()
![]()
Достаточность: Докажем, что для любого полностью определённого автомата Мили существует эквивалентный ему автомат Мура. Рассмотрим автомат Мили, с заданными алфавитами, описанный в виде графа
![]()
![]()
![]()



Таким образом получим граф, который описывает автомат
![]()
![]()
![]()
Докажем,
что автоматы
![]() и
и![]() эквивалентны. Для этого докажем, что
для любого состояния
эквивалентны. Для этого докажем, что
для любого состояния![]() автомата
автомата![]() существует эквивалентное ему состояние
существует эквивалентное ему состояние![]() автомата
автомата![]() и наоборот. Покажем, что для любого
состояния множества
и наоборот. Покажем, что для любого
состояния множества![]() существует эквивалентное из множества
существует эквивалентное из множества![]() .
.
![]() ;
;![]() ;
;![]() ;
;![]()
покажем обратное утверждение
![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]()
В связи с синтезом схем практический интерес представляет задача построения автомата, выполняющего заданный набор преобразований при минимальном числе внутренних состояний.
Тема 18.5. Примеры синтеза автоматов
Пример: Синтезировать автомат, на вход которого поступают в любом порядке и с любым числом повторений монеты достоинством 1, 2 и 3 руб. Автомат продаёт билет, если сумма опущенных монет равна 3. В случае превышения суммы автомат возвращает деньги.
Входной
алфавит
![]()
Выходной
алфавит
![]() ,
где
,
где
![]() – автомат выдаёт билет;
– автомат выдаёт билет;
![]() – автомат возвращает деньги;
– автомат возвращает деньги;
![]() – автомат ничего не делает.
– автомат ничего не делает.
Внутреннее
состояние автомата ассоциируем с суммой,
которую помнит автомат. Предполагая,
что после продажи билета и после возврата
денег автомат помнит нулевую сумму
![]() .
.
Задание автомата в виде графа будет выглядеть так:

Опишем автомат, задав его функцию переходов и функцию выходов:
|
|
|
|
|
| ||||
|
|
|
|
|
|
| |||
|
1 |
|
|
|
1 |
|
|
| |
|
2 |
|
|
|
2 |
|
|
| |
|
3 |
|
|
|
|
3 |
|
|
|
Пример: Синтезировать автомат, на вход которого подаются монеты достоинством 1, 2, 3 руб. Автомат выдаёт сигнал «Ч» - если сумма чётна, и «Н» - если сумма нечётна.
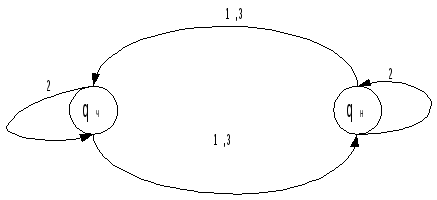
Сумма 0 считается чётной. Это автомат Мура, поскольку его выходной сигнал однозначно определяется состоянием, в которое автомат перешёл.
|
|
Н |
Ч |
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
