9

Лекция 13.

Тема 5. Введение в математический анализ. Функция одного переменного

Определение: Переменной величиной называется величина, которая принимает различные численные значения в некотором процессе. Переменные обычно обозначаются строчными буквами латинского алфавита x,y,z,…

Определение: пусть Х множество чисел и У множество чисел и пусть в силу некоторого правила каждому числу х  Х ставится в соответствие число у  У (одно или несколько), тогда говорят, что на множестве Х задана функция одного переменного и пишут у=f(x) (f – формальное определение правила вычисления функции, х- независимая переменная, у- зависимая переменная или функция).

Замечание: Функция – есть отображение элементов множества Х на множество У по закону f(x).

Определение: Х называется множеством определения функции, а У множеством значений.

Определение: Отображение(функция) называется однозначным, если из х₁≠ х₂ следует f(х₁)≠f(х₂) и наоборот.

Способы задания функций

1. Явный у=f(x) – y=x²

2, Неявный F(x,y)=0 - x² + y² - R² =0

3. Параметрический x=x(t) y=y(t) - x=4t y=3t²-5t, t-параметр .

4, Графический

5. Табличный.

Числовая последовательность.

Определение. Если каждому натуральному числу n поставлено в соответствие число х_n, то говорят, что задана последовательность

x_1, х₂, …, х_n = {x_n}

Общий элемент последовательности является функцией от n, т.е. каждому. числу n поставлено в соответствие число х_n

x_n = f(n)

Таким образом последовательность может рассматриваться как функция.

Задать последовательность можно различными способами – главное, чтобы был указан способ получения любого члена последовательности.

Пример. {x_n} = {(-1)ⁿ} или {x_n} = -1; 1; -1; 1; …

{x_n} = {sinn/2} или {x_n} = 1; 0; 1; 0; …

Для последовательностей можно определить следующие операции:

1. Умножение последовательности на число m: m{x_n} = {mx_n}, т.е. mx₁, mx₂, …

2. Сложение (вычитание) последовательностей: {x_n}  {y_n} = {x_n  y_n}.

3. Произведение последовательностей: {x_n}{y_n} = {x_ny_n}.

4. Частное последовательностей: 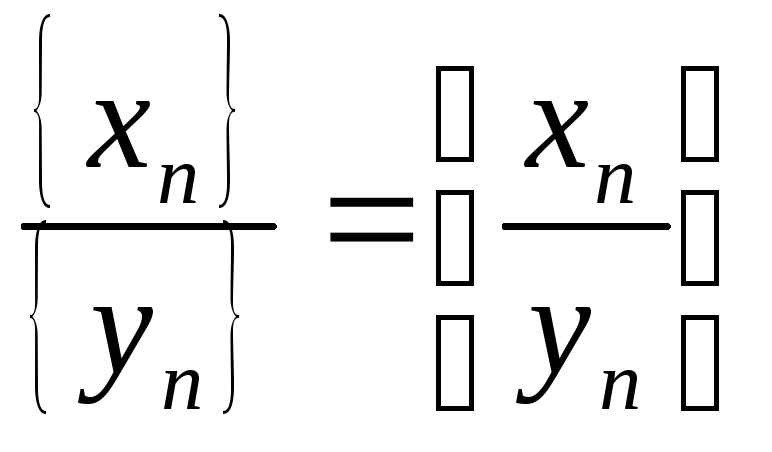при {y_n}  0.

Ограниченные и неограниченные последовательности.

Определение. Последовательность {x_n} называется ограниченной, если существует такое число М>0, что для любого n верно неравенство:

т.е. все члены последовательности принадлежат промежутку (-М; M).

Определение. Последовательность {x_n} называется ограниченной сверху, если для любого n существует такое число М, что

x_n  M.

Определение. Последовательность {x_n}называется ограниченной снизу, если для любого n существует такое число М, что

x_n  M

Пример. {x_n} = n – ограничена снизу {1, 2, 3, … }.

Определение. Число а называется пределом последовательности {x_n}, если для любого сколь угодно малого положительного числа >0 существует такой номер N, что для всех n > N выполняется условие:

Это записывается: lim x_n = a.

В этом случае говорят, что последовательность {x_n} сходится к а при n.

Свойство: Если отбросить какое- либо число членов последовательности, то получаются новые последовательности, при этом если сходится одна из них, то сходится и другая.

Пример. Доказать, что предел последовательности lim .

Пусть при n > N верно , т.е. . Это верно при, таким образом, если заN взять целую часть от , то утверждение, приведенное выше, выполняется.

Пример. Показать, что при n последовательность 3, имеет пределом число 2.

Итак: {x_n}= 2 + 1/n; 1/n = x_n – 2

Очевидно, что существует такое число n, что , т.е.lim {x_n} = 2.

Теорема. Последовательность не может иметь более одного предела.

Доказательство. Предположим, что последовательность {x_n} имеет два предела a и b, не равные друг другу.

x_n  a; x_n  b; a  b.

Тогда по определению существует такое число  >0, что

Запишем выражение:

А т.к. - любое число, то , т.е.a = b. Теорема доказана.

Теорема. Если x_n  a, то .

Доказательство. Из x_n  a следует, что . В то же время:

, т.е. , т.е.. Теорема доказана.

Теорема. Если x_n  a, то последовательность {x_n} ограничена.

Следует отметить, что обратное утверждение неверно, т.е. из ограниченности последовательности не следует ее сходимость.

Например, последовательностьне имеет предела, хотя