
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
ПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Начала анализа
Индивидуальные задания
-
Пособие разработано ст. преп. Савочкиной А. А., доцентом Брагиной Н. А..
Одобрено методической комиссией кафедры «Высшая математика»
© 2007, каф. «Высшая математика» ПГТУ
Пермь 2007 Вариант решения заданий
-
Вычислить предел последовательности
![]() .
.
Решение. Распишем факториалы, стоящие
в числителе и знаменателе через
наименьший, то есть через
![]() .
.
 Ответ.
0.
Ответ.
0.
-
Доказать, что .
Решение. По определению, предел
функции
![]() при
при
![]() равен 7, если для любого
равен 7, если для любого
![]() существует такое
существует такое
![]() ,
что для всех
,
что для всех
![]() из
из
![]() - окрестности точки
- окрестности точки
![]() таких, что
таких, что
![]() справедливо неравенство:
справедливо неравенство:
![]()
Тогда
![]() .
Следовательно, разность между значениями
функции и числом 7 меньше
.
Следовательно, разность между значениями
функции и числом 7 меньше
![]() для всех
для всех
![]() из
из
![]() окрестности точки
окрестности точки
![]() .
Тем самым утверждение, что
.
Тем самым утверждение, что
![]() доказано.
доказано.
-
Вычислить пределы функций.
А) Найти
![]()
Решение. Прежде всего, проверим,
применимы ли к данной дроби теоремы о
пределах, или мы имеем дело с
неопределенностью. Для этого найдем
пределы числителя и знаменателя дроби.
Функции
![]() и
и
![]() являются бесконечно большими. Поэтому,
являются бесконечно большими. Поэтому,
![]() .
Следовательно, имеем дело с неопределенностью
вида
.
Следовательно, имеем дело с неопределенностью
вида
![]() .
.
Для раскрытия этой неопределенности
выделим в числителе и в знаменателе
![]() в старшей для числителя и знаменателя
степени в качестве сомножителя и сократим
дробь.
в старшей для числителя и знаменателя
степени в качестве сомножителя и сократим
дробь.

Ответ. 0.
Б) Найти
![]()
Решение. Для раскрытия неопределенности
![]() в этом случае, нужно разложить числитель
и знаменатель на множители и сократить
дробь на общий множитель.
в этом случае, нужно разложить числитель
и знаменатель на множители и сократить
дробь на общий множитель.
![]()
Ответ. -9.
В) Найти
![]() .
.
Решение. Для раскрытия неопределенности
![]() в этом случае, нужно умножить числитель
и знаменатель на выражение, сопряженное
числителю, а затем сократить дробь на
общий множитель.
в этом случае, нужно умножить числитель
и знаменатель на выражение, сопряженное
числителю, а затем сократить дробь на
общий множитель.
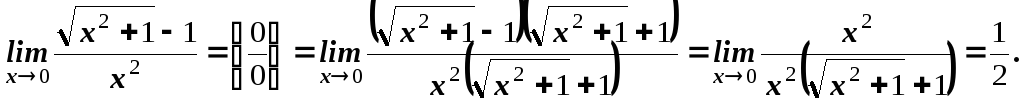
Ответ.
![]() .
.
Г) Найти
![]()
Решение. Для раскрытия неопределенности
![]() в этом случае, нужно выделить первый
замечательный предел:
в этом случае, нужно выделить первый
замечательный предел:
![]()
![]()
Ответ. k.
Д) Найти
![]() .
.
Решение. Для раскрытия неопределенности
![]() в этом случае, нужно выделить второй
замечательный предел:
в этом случае, нужно выделить второй
замечательный предел:![]() .
.
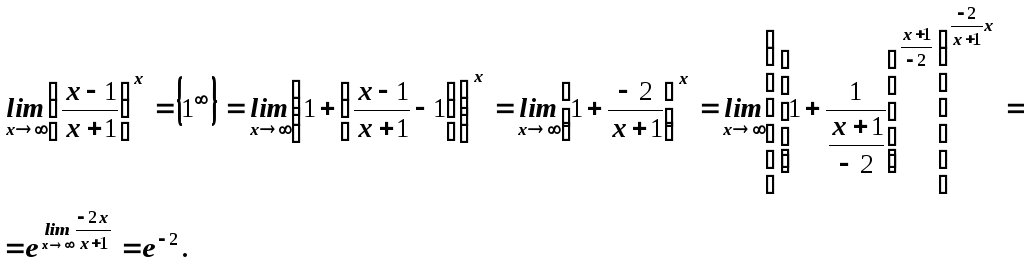
Ответ.
![]() .
.
Е) Найти
![]() .
.
Решение. Вычисление предела связано
с раскрытием неопределенности вида
![]() .
Для раскрытия этой неопределенности
нужно разность преобразовать в частное,
то есть неопределенность
.
Для раскрытия этой неопределенности
нужно разность преобразовать в частное,
то есть неопределенность
![]() свести к неопределенности
свести к неопределенности
![]() или
или
![]() .
Для этого необходимо избавится от
иррациональности. Умножим и разделим
выражение
.
Для этого необходимо избавится от
иррациональности. Умножим и разделим
выражение
![]() на выражение
на выражение
![]() и воспользуемся формулой разности
квадратов.
и воспользуемся формулой разности
квадратов.
 .
.
Ответ.
![]() .
.
Ж) Найти
![]()
Решение. Для раскрытия неопределенности
![]() в этом случае, нужно произведение
преобразовать в частное, то есть
неопределенность
в этом случае, нужно произведение
преобразовать в частное, то есть
неопределенность
![]() свести к неопределенности
свести к неопределенности
![]() или
или
![]() .
.
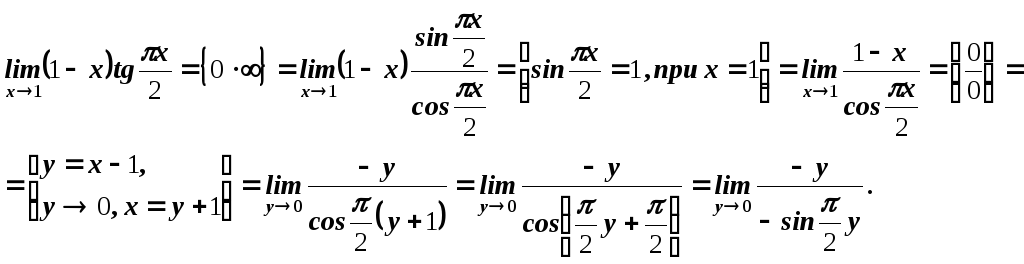
Выделяем первый замечательный предел,
то есть умножаем числитель и знаменатель
на
![]() .
Получаем,
.
Получаем,
 .
.
Ответ.
![]() .
.
З) Найти
![]()
Решение. Для раскрытия неопределенности
![]() в этом случае, нужно выделить второй
замечательный предел:
в этом случае, нужно выделить второй
замечательный предел:
![]() .
.

Ответ.
![]() .
.
И) Найти
![]() .
.
Решение. Для раскрытия неопределенности
![]() ,
нужно в числителе и в знаменателе
выделить множитель
,
нужно в числителе и в знаменателе
выделить множитель
![]() .
Для этого числитель и знаменатель
разделим на
.
Для этого числитель и знаменатель
разделим на
![]() :
:
![]() .
.
![]() =
=![]()
Ответ.
![]() .
.
-
Указать характер точек разрыва функции .
Решение. Найдем левый и правый предел
функции в точке
![]() .
.
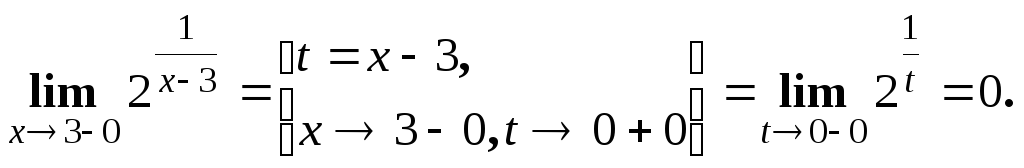
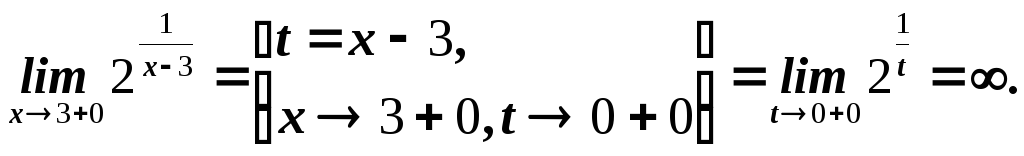
Левый предел конечен и равен 0, а правый
бесконечен. Тогда, по определению,
![]() - точка разрыва второго рода.
- точка разрыва второго рода.
Вариант 1
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
е)
![]() ; д)
; д)
![]()
ж)
![]() ; з)
; з)
![]() ;
;
и)
![]() .
.
4. Указать характер точек разрыва функции.
![]() .
.
Вариант 2
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ; з)
; з)
![]() ;
;
и)
![]() .
.
4. Указать характер точек разрыва функции.
![]() .
.
Вариант 3
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
3. Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ; з)
; з)
![]() ;
;
и)
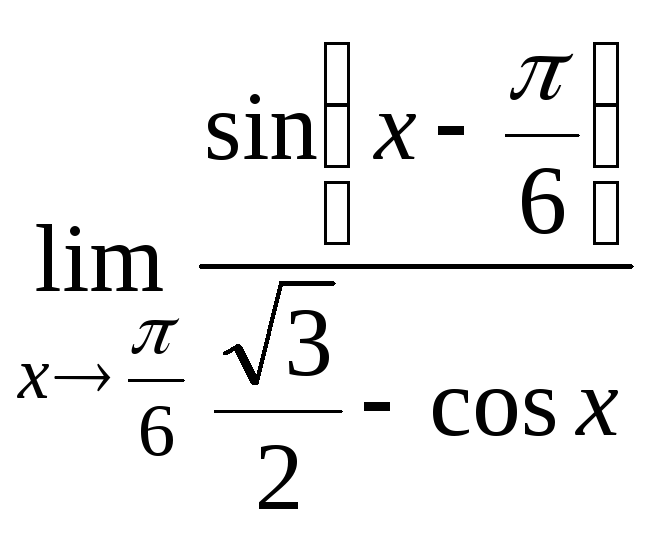 .
.
4. Указать характер точек разрыва функции.
![]() .
.
Вариант 4
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ; з)
; з)
![]() ;
;
и)
![]() .
.
4. Указать характер точек разрыва функции.
![]() .
.
Вариант 5
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
 ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ; з)
; з)
![]() );
);
и)
![]() .
.
4. Указать характер точек разрыва функции.
![]() .
.
Вариант 6
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
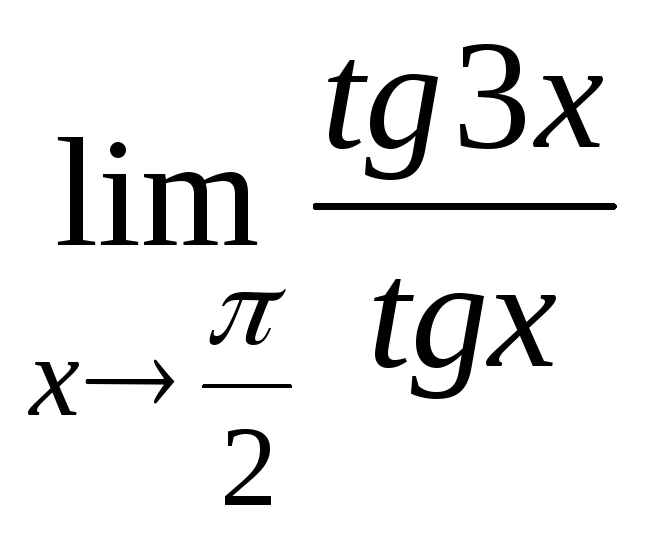 ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ;
з)
;
з)
![]() ;
;
и)
![]() .
.
4. Указать характер точек разрыва функции.
![]() .
.
Вариант 7
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
 ; з)
; з)
![]() ;
;
и)
![]() .
.
4. Указать характер точек разрыва функции.
![]() .
.
Вариант 8
-
Вычислить предел последовательности
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
 ;
;
ж)
![]() ; з)
; з)
![]() ;
;
и)
![]() .
.
4. Указать характер точек разрыва функции.
![]() .
.
Вариант 9
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ; з)
; з)
 ;
;
и)
![]() .
.
3. Указать характер точек разрыва функции.
![]() .
.
Вариант 10
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ; з)
; з)
![]() ;
;
и)
![]() .
.
4. Указать характер точек разрыва функции.
![]()
Вариант 11
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
 ;
;
д)
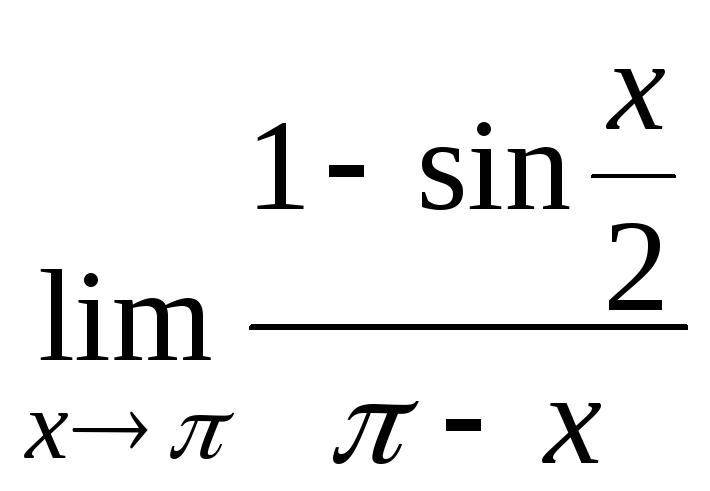 ; е)
; е)
![]() ;
;
ж)
![]() ; з)
; з)
![]() ;
;
и)
![]() .
.
4. Указать характер точек разрыва функции.
![]()
Вариант 12
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ; з)
; з)
![]() ;
;
и)
![]() .
.
4. Указать характер точек разрыва функции.
![]() .
.
Вариант 13
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ; з)
; з)
![]() ;
;
и)![]() ;
;
4. Указать характер точек разрыва функции.
![]() .
.
Вариант 14
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ; з).
; з).
![]() ;
;
и)
![]() .
.
4. Указать характер точек разрыва функции.
![]()
Вариант 15
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
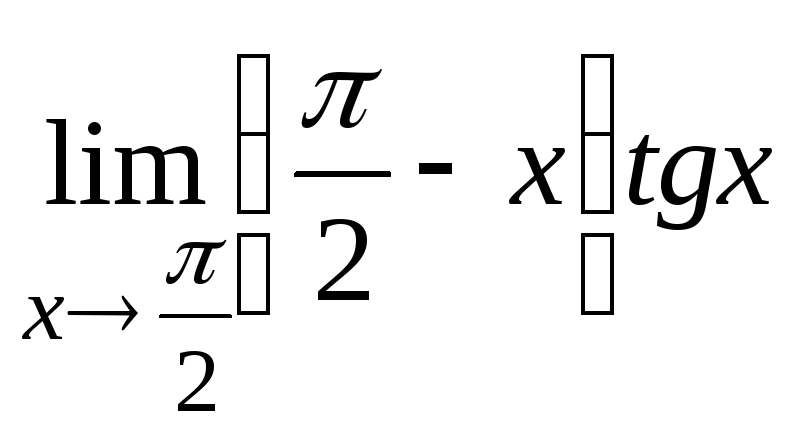 ; з)
; з)
![]() ;
;
и)
![]() .
.
3. Указать характер точек разрыва функции.
![]()
Вариант 16
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ; з)
; з)
![]() ;
;
и)
![]() .
.
4. Указать характер точек разрыва функции.
![]()
Вариант 17
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
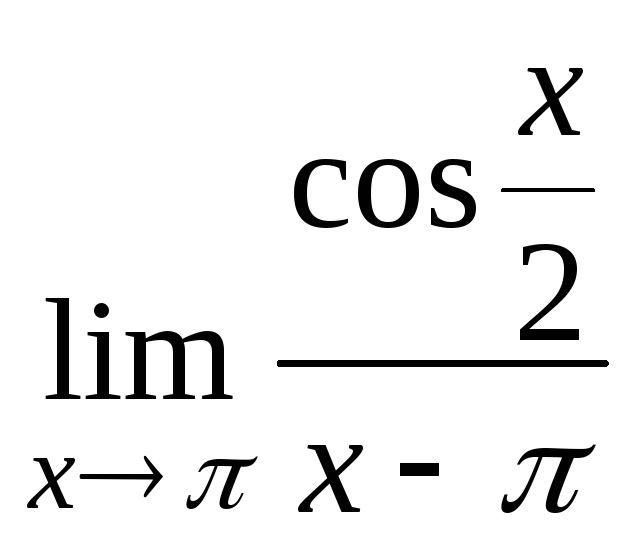 ; з)
; з)
![]() ;
;
и)
![]() .
.
4. Указать характер точек разрыва функции.
![]() .
.
Вариант 18
-
Вычислить предел последовательности.
![]()
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ; з)
; з)
![]() ;
;
и)
![]() .
.
4. Указать характер точек разрыва функции.
![]() .
.
Вариант 19
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ; з)
; з)
![]() ;
;
и)
![]() .
.
4. Указать характер точек разрыва функции.
![]() .
.
Вариант 20
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ; з)
; з)
![]() ;
;
и)
![]() .
.
4. Указать характер точек разрыва функции.
![]() .
.
Вариант 21
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ; з)
; з)
![]() ;
;
и)![]() .
.
4. Указать характер точек разрыва функции.
![]() .
.
Вариант 22
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ; з)
; з)
![]() ;
;
и)![]() .
.
4. Указать характер точек разрыва функции.
![]() .
.
Вариант 23
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ; з)
; з)
![]() ;
;
и)
![]() .
.
4. Указать характер точек разрыва функции.
![]() .
.
Вариант 24
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ; з)
; з)
![]() ;
;
и)
![]() .
.
4. Указать характер точек разрыва функции.
![]() .
.
Вариант 25
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ; з)
; з)
![]() ;
;
и)![]() .
.
4. Указать характер точек разрыва функции.
![]() .
.
Вариант 26
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ; з)
; з)
![]() ;
;
и)![]() .
.
4. Указать характер точек разрыва функции.
![]() .
.
Вариант 27
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ; з)
; з)
![]() ;
;
и)
![]() .
.
4. Указать характер точек разрыва функции.
![]() .
.
Вариант 28
-
Вычислить предел последовательности.
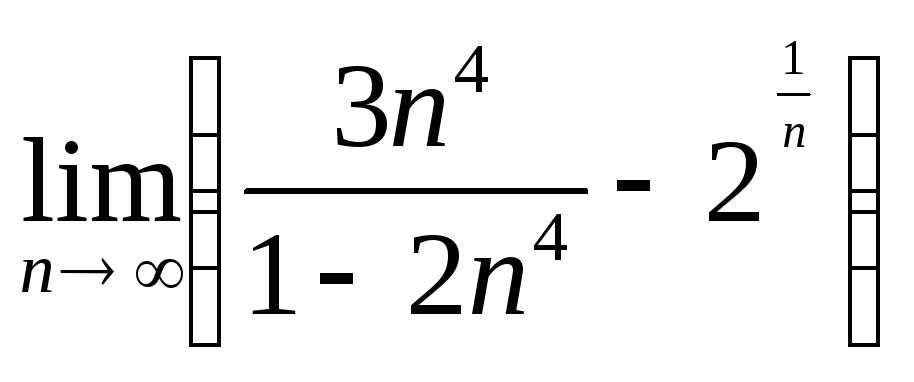 .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ; з)
; з)
![]() ;
;
и)![]() .
.
4. Указать характер точек разрыва функции.
![]() .
.
Вариант 29
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ; з)
; з)
![]() ;
;
и)
![]() .
.
4. Указать характер точек разрыва функции.
![]() .
.
Вариант 30
-
Вычислить предел последовательности.
![]() .
.
-
Доказать по определению предела.
![]() .
.
-
Вычислить пределы функций.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ; з)
; з)
![]() ;
;
и)
![]() .
.
4. Указать характер точек разрыва функции.
![]() .
.
