15.2.1. Построение перпендикуляра к заданной прямой
Дана прямая m, лежащая в предметной плоскости. Ее перспективное изображение начинается в точке 1 и идет в точку схода Fm (рис. 15.6).
В предметной плоскости начертим перпендикуляр n к прямой m. Проводя из точки зрения S проецирующий луч, параллельный прямой n, получим точку схода Fn .
Луч зрения SFm , идущий в точку схода Fm , параллелен прямой m.
Прямые m и n взаимно перпендикулярны, следовательно, лучи зрения SFm и SFn также взаимно перпендикулярны, то есть треугольник SFmFn – прямоугольный с прямым углом при вершине S.
Совмещаем треугольник SFmFn с картиной, вращая его вокруг h. Получаем на картине совмещенный прямоугольный треугольник S0FmFn с прямым углом при совмещенной точке зрения S0 (рис. 15.7).
Таким образом, чтобы найти точку схода Fn всех прямых n, перпендикулярных к заданной прямой m, надо отметить на картине совмещенную точку зрения S0 (засечка циркулем на рис. 15.7) и провести катет S0Fm . Второй катет S0Fn указывает искомую точку схода Fn .
Любые прямые, сходящиеся в точки Fn и Fm , взаимно перпендикулярны.
15.2.2. Построение произвольного угла
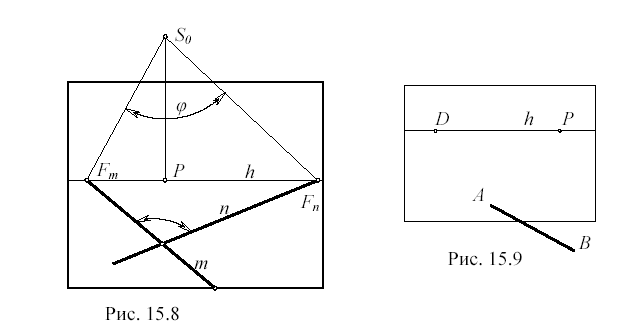
Если прямые m и n на рис. 15.6 пересекаются под произвольным углом φ, то проецирующие лучи SFm и SFn образуют между собой точно такой же угол. Поэтому угол при вершине S0 совмещенного треугольника S0FmFn равен углу φ между прямыми m и n (рис. 15.8).
Следовательно, чтобы в перспективе начертить прямую n под углом φ к заданной прямой m, надо построить совмещенный треугольник с углом φ при вершине S0 (см. рис. 15.8). Высота PS0 совмещенного треугольника равна дистанционному расстоянию.
Любая прямая в предметной плоскости, идущая в найденную точку схода Fn , пересекает прямую m под заданным углом φ.
15.2.3. Пример
Построить квадрат в перспективе, считая данный отрезок AB, лежащий в предметной плоскости, его стороной. Линия горизонта, главная точка картины и дистанция известны (рис. 15.9).
Решение
Способом совмещения найдем точку схода Fn для всех прямых, перпендикулярных к заданному отрезку. Для этого находим точку схода F отрезка AB и строим совмещенную точку зрения S0 , откладывая вверх от главной точки дистанционное расстояние. Вершина Fn вспомогательного прямоугольного треугольника S0FFn и является искомой точкой схода (рис. 15.10).
Отправляя лучи из концов отрезка AB в найденную точку схода Fn , получаем направления боковых сторон квадрата.
Диагональ BC квадрата составляет угол 45° со стороной AB, поэтому во вспомогательном треугольнике S 0FFn откладываем угол 45° и находим точку схода F45 диагонали квадрата. Зная направление диагонали, достраиваем квадрат.
15.3. Реконструкция перспективы
Реконструкция перспективы – построение ортогонального чертежа (плана и фасада) объекта, изображенного в перспективе.
Если известны все элементы перспективы (главная точка, дистанция, линия горизонта, основание картины), то восстановление ортогональных проекций не вызывает затруднений. Построение плана рассмотрено в параграфе “Определение длины отрезка по плану”, а высотные отметки находят “выносом на картину” вертикальных ребер объекта.
Но если на картине не заданы некоторые параметры (например, неизвестна главная точка картины или дистанционное расстояние), то для реконструкции перспективы потребуются дополнительные сведения о форме изображаемого объекта. На картине должно быть изображение геометрической фигуры, имеющей четко выраженную геометрическую форму: квадрат, прямоугольник (с известным отношением сторон), два прямых угла, отрезки параллельных прямых. В этом случае мы сумеем определить недостающие компоненты начерченной перспективы.
Пусть на картине есть изображение квадрата ABCE, лежащего в предметной плоскости (рис. 15.11). Задана линия горизонта и основание картины. Требуется определить (реконструировать) положение главной точки и дистанционное расстояние.
Продлив стороны квадрата, получаем точки схода F и F' взаимно перпендикулярных сторон квадрата (рис. 15.12). Совмещенная точка зрения S0 и точки F, F' должны образовать прямоугольный треугольник (см. рис. 15.10). Множество точек S0 , удовлетворяющих этому условию, образует полуокружность. Начертим ее на картине.
Продлив взаимно перпендикулярные диагонали квадрата, получаем еще две точки схода FД и FД'. На отрезке FДF', как на диаметре, чертим полуокружность (см. рис. 15.12).
Опуская перпендикуляр из этой точки на линию горизонта, получаем главную точку картины. Расстояние PS0 равно искомому дистанционному расстоянию.