Лекции. Начертательная геометрия. 1 семестр / Лекция № 1 арх

Лекция №1  

Предмет начертательной геометрии

Начертательная геометрия является одним из разделов геометрии, в которой пространственные формы предметов, изучаются по их изображениям. Существует крылатое выражение «чертеж - международный язык техники, начертательная геометрия – грамматика этого языка». Умение читать и изготавливать чертеж для всех технических работников такая же необходимость как владение простой грамотностью.

КРАТКАЯ ИСТОРИЧЕСКАЯ СПРАВКА.

Начертательная геометрия, как наука, возникла в конце 18 века. основателем этой науки стал французский инженер и ученый Гаспар Монж (1746 – 1818г). Он привел в стройную систему известные в то время методы изображений, придав им глубокое теоретическое обоснование, создал свой метод изображений, который используется в настоящее время.

Преподавание этой дисциплины в России началось в 1810 году в Петербургском институте корпуса инженеров путей сообщения. В качестве преподавателей были приглашены французских инженеры.

ЦЕЛИ И ЗАДАЧИ ИЗУЧЕНИЯ ДИСЦИПЛИНЫ

Методы начертательной геометрии являются теоретической базой для решения задач технического черчения. В технике чертежи являются основным средством выражения человеческих идей. Они должны не только определять форму и размеры предметов, но и быть достаточно простыми и точными в графическом исполнении, помогать всесторонне исследовать предметы и их отдельные детали. Для того чтобы правильно выразить свои мысли с помощью рисунка, эскиза, чертежа требуется знание теоретических основ построения изображений геометрических объектов, их многообразие и отношения между ними, что и составляет предмет начертательной геометрии.

Задачи начертательной геометрии можно разбить на две группы:

А) Учебные.

1. Изучение алгоритмов графического отображения трехмерных фигур на плоском двухмерном чертеже (умение выполнять чертеж).

2. Изучение способов решения позиционных и метрических задач. Задачи называются позиционными, если требуется определить видимость элементов фигуры, их взаимное расположение или изменить положение фигур. Метрическими называются задачи на определение метрических характеристик фигур ( длина, площадь, угол и т.д

Б) Научные.

1. Исследование моделей плоских и пространственных образов в трехмерном и многомерном пространстве.

2. Развитие способов построения и реконструкции изображения

Теория изображений, составляет основу начертательной геометрии. Правила построения изображений основаны на методе проекций. Поэтому проекционный метод построения изображений является основным методом начертательной геометрии.

Изображение, которое позволяет определять взаимосвязь (взаимопринадлежность) элементов объекта, называют полным.

Изображения, по которым можно определить размеры объекта, называется метрически определенными.

В начертательной геометрии приняты следующие условные обозначения:

1.Обозначения изображаемых фигур:

A, B, C… 1, 2, 3, 4… - точки.

a, b, c, d…. . - прямые и кривые линии.

Θ, Λ, Σ, Ω.. - поверхности (плоскости)

2. Знаки некоторых геометрических операций:

≡ знак совпадения двух геометрических фигур;

║ параллельность,

∩ пересечение,

є взаимная принадлежность,

┴ перпендикулярность

МЕТОДЫ ПРОЕЦИРОВАНИЯ

Любой предмет можно рассматривать как множество точек, его составляющих. Поэтому проецирование предмета на плоскость или поверхность сводится к проецированию на плоскость или поверхность отдельных его точек.

Проецированием называется проведение через точки изображаемого предмета проецирующих лучей до пересечения их с выбранной плоскостью или поверхностью.

ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ

Для построения изображения используется плоскость- эта плоскость называется плоскостью проекций. Выберем в пространстве поизвольную точку S в качестве центра проецирования и плоскость проекций П₁, не проходящую через точку S, в качестве плоскости проекций. Чтобы спроецировать точку А и В на плоскость П₁, через центр проецирования S, проведем проецирующие лучи SA и SB до пересечения с плоскостью проекций. Точка имеет на плоскости П₁ единственную проекцию, так как проецирующая прямая пересекается с плоскостью П₁ в одной точке. Так, точка А имеет на плоскости П₁ единственную проекцию А₁, отрезок [АВ] - единственную проекцию [А₁В₁], любая геометрическая фигура - единственную проекцию.

Описанные построения выражают суть операции, называемой центральным проецированием точек пространства на плоскость. Центральное проецирование есть наиболее общий случай проецирования геометрических объектов на плоскости. По принципу центрального проектирования работают фотоаппараты и кинокамеры, выполняют наглядные перспективные изображения.

Рисунок 1.

П₁-плоскость проекций

S - центр проецирования

А, В – точки в пространстве

А₁, В₁ – центральные проекции точек

S А_{1 ,} S В₁ -центральные проецирующие лучи.

ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ

Если центр проецирования S удалить в бесконечность, проецирующие лучи можно рассматривать как параллельные проецирующие прямые. Положение проецирующих прямых относительно плоскости проекций определяется направлением проецирования S (рис.2). Полученные изображения А₁ и В₁ называются параллельными проекциями точек А и В.

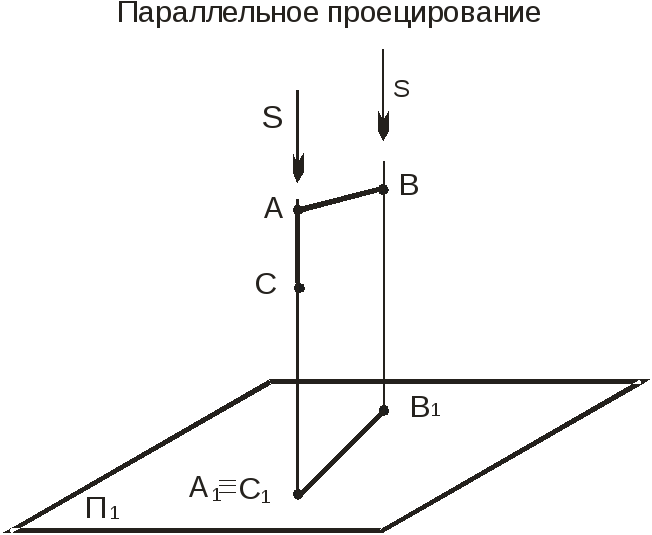
Рисунок 2.

П₁-плоскость проекций

S – направление проецирования

А, В – точки в пространстве

А₁, В₁ – параллельные проекции точек

А А_{1 ,} ВВ₁ - параллельные проецирующие лучи

Параллельные проекции подразделяются на ортогональные, когда проецирующие лучи перпендикулярны плоскостям, и косоугольные, в случае, когда проецирующие лучи образуют с плоскостью проекций угол не равный 90⁰. Косоугольное проецирование используется при построении аксонометрических проекций.

СВОЙСТВА (ИНВАРИАНТЫ) ЦЕНТРАЛЬНОГО И ПАРАЛЛЕЛЬНОГО ПРОЕЦИРОВАНИЯ

Основными и неизменными свойствами центрального и параллельного проецирования являются следующие свойства:

1) проекция точки – точка;

проекция прямой – прямая, в частном случае, если пряма проецирующая, – точка;

проекция плоской фигуры – в частном случае, - прямая;

проекция трехмерного объекта – плоская фигура.

2) принадлежность, если точка принадлежит прямой, то проекция этой точки

принадлежит проекции этой прямой;

3) непрерывность;

4) пропорциональность.

К проекционным изображениям в начертательной геометрии предъявляются следующие основные требования:

Обратимость- восстановление оригинала по его проекционному изображению (чертежу) – возможность определять форму и размеры предметов, его положение и связь с окружающими объектами;

Точность – графические операции, выполненные на чертеже, должны давать точные результаты;

Простота – изображение должно быть простым по построению и должно допускать однозначные описания объекта в виде последовательности графических операций.

МЕТОД МОНЖА

Предложенный Г.Монжем метод построения изображений основывается на ортогональном проецировании объекта на взаимно перпендикулярные плоскости проекций. Этот метод обеспечивает обратимость и метрическую определенность изображений.

Рассмотрим в пространстве точку и плоскости проекций. Наглядное изображение на рис.3. демонстрирует суть метода Монжа. В дальнейшем будем использовать наглядные изображения для лучшего представления объектов.

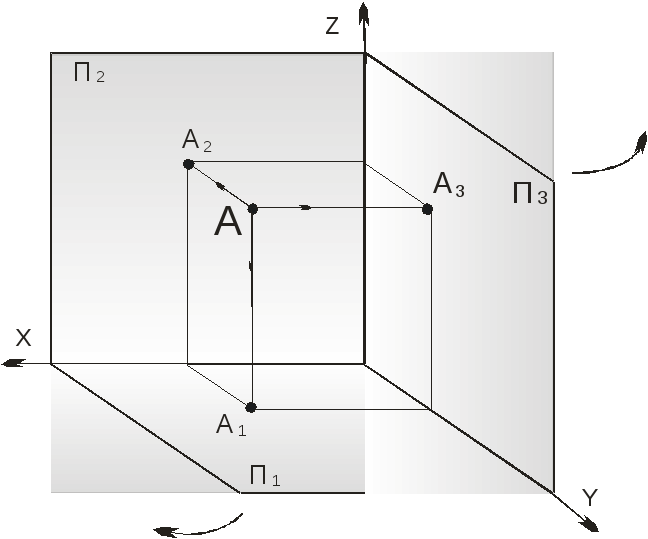
Рисунок 3.

П₁- горизонтальная плоскость проекций

П₂- фронтальная плоскость проекций

П₃- профильная плоскость проекций

А – точка в пространстве

А₁ – горизонтальная проекция точки

А₂ – фронтальная проекция точки

А₃ – профильная проекция точки

А А₁ – горизонтально проецирующий луч

А А₂ – фронтально проецирующий луч

А А₃ – профильно-проецирующий луч

Линии пересечения плоскостей проекций являются осями координат. Линии связи всегда перпендикулярны осям координат.

Перейдем от наглядного изображения к проекциям. Для этого мысленно разрежем плоскости проекций по оси Y, плоскость П₁ и П₃ совместим с вертикальной плоскостью. Полученное изображение (рис. 4) называется эпюр Монжа или ортогональный чертеж точки А. На эпюре нет самой точки, - только ее проекции, которые соединены линиями связи.

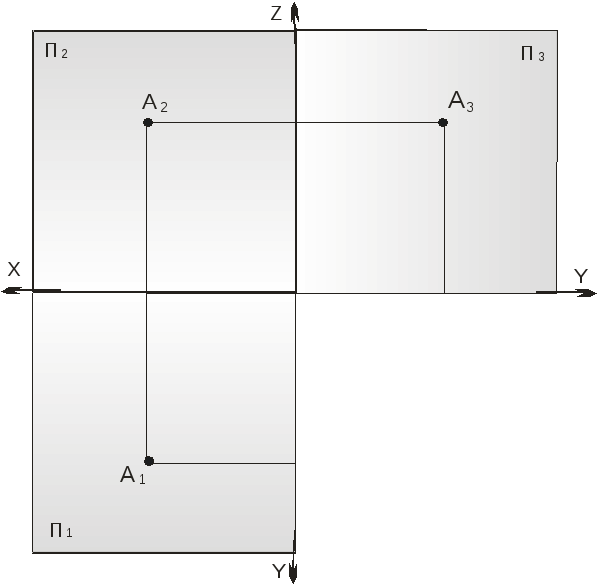
Рисунок 4