1. Действительные числа

Понятие действительного числа является одним из основных математических понятий. Свойства действительных чисел служат тем фундаментом, на котором строится теория пределов, а вместе с ней и весь современный математический анализ. Существуют различные подходы к определению действительного числа (теории Дедекинда, Кантора и другие). Однако наиболее логичным и простым является аксиоматический метод введения действительного числа.

Определение 1.1.СовокупностьRиз более чем одного элемента называетсямножеством действительных чисел, если:

а) в множестве Rопределена операция сложения элементов, сопоставляющая каждой паре элементовx, y є Rнекоторый элемент изR, называемый их суммой и обозначаемыйх+у, такой, что выполняются следующие условия (аксиомы):

1а) х+у=у+хдля любыхх, у є R;

2а) х+(у+z)=(х+у)+zдля любыхх,у,z є R;

3a) вRсуществует такой элемент, называемыйнулем и обозначаемый 0, чтох+0=хдля всехх є R;

4a) для любогох є Rсуществует элемент изR, называемыйпротивоположным хи обозначаемый -х, для которогох+(-х)=0;

б) в множестве Rопределена операция умножения элементов, сопоставляющая каждой паре элементовх, у є Rнекоторый элемент изR, называемый их произведением и обозначаемыйху, такой, что выполняются следующие условия (аксиомы):

1б) ху=ухдля любыхх, у є R;

2б) х (уz)=(ху) zдля любыхх, у, z є R;

3б) в Rсуществует такой элемент, называемый единицей и обозначаемый1, чтох·1=х, для всехх є R;

4б) для любого Rэлементах≠0существует элемент изR, называемый обратным к х и обозначаемыйилидля которого;

в) операции сложения и умножения удовлетворяют условию (аксиоме):

1 в) (х+у)z=хz+уzдля всехх, у, z є R;

г) в множестве R определено отношение порядка<, определяемое следующим образом: любые два различныч элементах, у, є Rсвязаны либо отношениемх < у, или, что то же самоеу > х, либо отношениему < х, или, что то же самоех > у, причем выполняются следующие условия (аксиомы):

1 г) если х<yиy<z, тох<z;

2 г) если х<y, то для любого имеет местоx+z<y+z;

3 г) если х<yиz>0, тоxz<yz;

д) для любых непустых множеств Х, У Rтаких, что для каждой пары элементовх є Хиу є Увыполняется условиех ≤ у(либох < у, либох=у), вRсуществует элементz, удовлетворяющий условию

Элементы множества R называютсядействительными или вещественными числами. Аксиомы групп а), б), в) есть аксиомы сложения и умножения действительных чисел, аксиомы группы г) – аксиомы сравнения действительных чисел, а аксиома группы д) – аксиома непрерывности.

Теорема 1.1.Числа0,-х,1иединственны.

Докажем, например, единственность нуля (остальные утверждения проверяются аналогично). Допустим, что существуют два нуля 0и0^/. Тогда, согласно аксиоме 3(а),0+0^/=0и0^/+0=0^/.В силу аксиомы (а) левые части этих равенств одинаковы, следовательно, одинаковы и правые, т.е.0=0^/

Число х+(-у)называетсяразностьючиселх иуобозначаетсях-у. Число, где, называютсячастным от деленияхиуи обозначаетсяили. Соотношенияназывается неравенствами. Числох, удовлетворяющее неравенствух>0, называют положительным, а числох, удовлетворяющее неравенствух<0, называют отрицательным.

Числа 1,и т.д. называются натуральными числами, а их множество обозначаетсяN. Числаназываются целыми числами, их множество обозначаютZ. Числа вида, гдеmиn- целые, а, называются рациональными числами, их множество обозначаетсяQ. Действительные числа, не являющиеся рациональными, называют иррациональными, а их множествообозначаютI.

Теорема 1.2.(Плотность действительных чисел). Для любых двух различных действительных чиселхиу, существует такое числоz, что.

Доказательство.Пусть. Отсюда по аксиоме 2(г)или в силу аксиом 1(а) и 3(б)или согласно 1(в)или на основании 1(б) и 1(г) или, наконец, по аксиоме 3(г)т.е. в качестве числаzможно взять.

Доказывается, что любое действительное число можно представить в виде бесконечной десятичной дроби а,а₁а₂……а_n…..,гдеа- любое целое число,а₁, а₂…….а_n– целые числа, принимающие значения0,1….9. При этом все рациональные числа изображаются периодическими десятичными дробями, а иррациональные числа - непериодическими десятичными дробями.

Геометрически множество действительных чисел изображается числовой осью, т.е. прямой, не которой заданы начало отсчета, единица масштаба и положительное направление, а отдельные числа – точками этой оси. Поэтому совокупность действительных чисел часто называют числовой осью, а отдельные числа – ее точками. Введем на числовой оси декартову систему координат, взяв в качестве начала координат начало отсчета, а в качестве единичного вектора - вектор, длина которого равна единице масштаба, а направление совпадает с положительным направлением числовой оси. Прямую с заданной декартовой системой координат будем называть координатной осью.

Определение 1.2.Абсолютной величиной или модулем действительного числа х называется неотрицательное число, определенное формулой

.

Отметим ряд свойств модуля.

1. 

В самом деле, по определению модуля и свойству неравенств

при мы имеем:

а при :.

2. .

Для доказательства воспользуемся очевидными неравенствами:

.

Почленное сложение этих неравенств дает

.

По свойству 1) полученное двойное неравенство равносильно неравенству

.

3. .

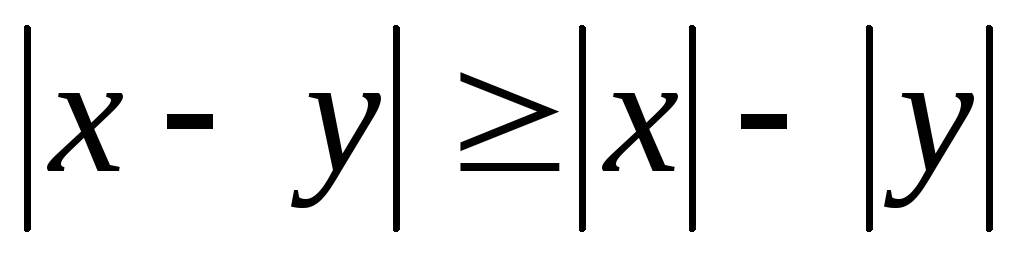В самом деле, для любых чисел хиуимеем:

Отсюда по свойству 2) или.

4. ,.

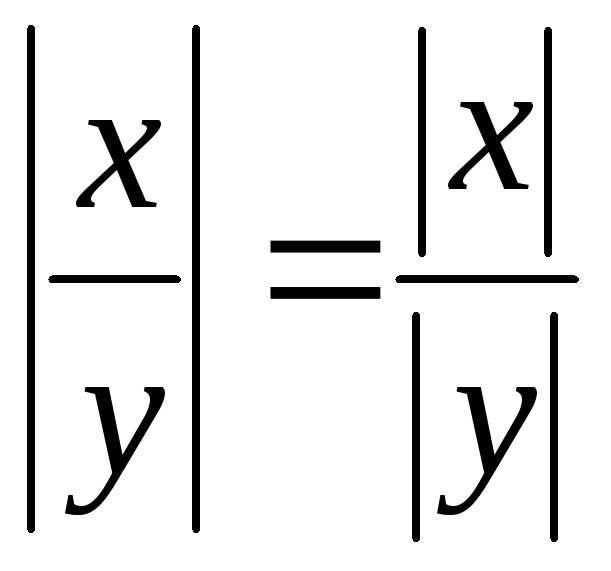Эти равенства легко проверяются путем рассмотрения различных комбинаций знаков чисел хиу.

Пополним множество действительных чисел тремя элементами -∞,+∞,∞, определив их соответственно условиями:,. Бесконечностиназываются также бесконечно удаленными точками в отличие от остальных точек, которые называются конечными точками числовой оси. Множество действительных чиселR, дополненное элементамиибудем называтьрасширенным множеством действительных чисели обозначать

Рассмотрим некоторые важные типы подмножеств расширенного множества действительных чисел . Пусть. Множествоназываетсяотрезкомилисегментом, множество- интервалом, множества- полуинтервалами.