Декартова прямоугольная система координат

Базис называется ортонормированным, если его векторы попарно ортогональны и по длине равны единицам.

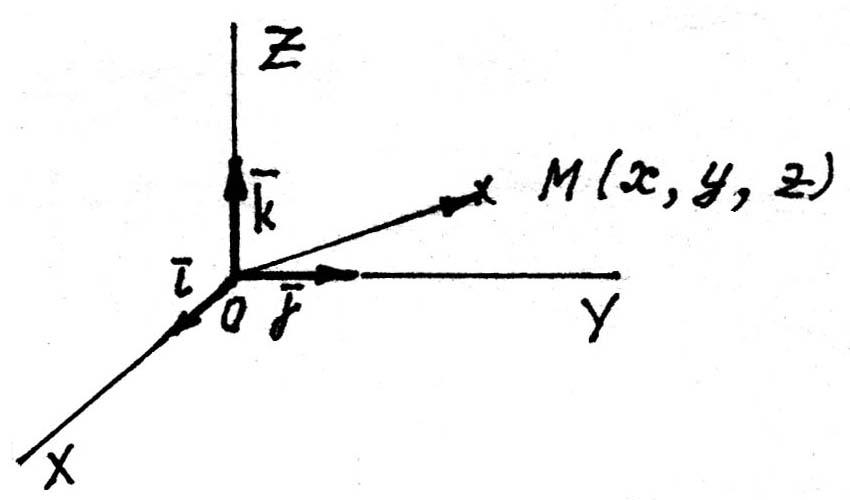Система координат, базис которой ортонормирован, называетсядекартовой прямоугольной системой координат.

Рис. 9

Базисные векторы такой системы называютсяортами и обозначаются соответственно ,,(рис. 9). Оси идущие в направлении базисных векторов соответственноOX – ось абсцисс, OY – ось ординат, OZ – ось аппликат. Система координат называется правой, если кратчайший поворот первого базисного вектора до совмещения со вторым базисным векторомсмотрится с конца третьего базисного векторапроисходящим против хода часовой стрелки. В противном случае имеемлевую систему координат. Нетрудно видеть (рис. 10), что координатами вектора , равно как и точкиМ, являются проекции на координатные оси.

Рис. 10

Тогда , аналогично , . Теперь радиус-вектор или , где – координаты радиус-вектора , а ,, - составляющие или компоненты этого вектора. .

Поскольку, например, , а . Теперь . , где - угол между вектором и осью OX. Теперь , аналогично,, гдеи- углы междуи осямиOY и OZ соответственно. Приведенные косинусы называются направляющими косинусами радиуса вектора .

Если - произвольный вектор иX, Y, Z – его проекции на оси, то перенося начало в точкуО, будем иметь ,,,,.

Если вектор задан координатами начала и конца, тои расстояниемежду точкамиА и В будет .

Скалярное произведение двух векторов

Углом между двумя векторами называется угол, на который нужно повернуть один вектор до совмещения с другим кратчайшим образом. Из такого определения угла следует, что .

Скалярным произведением двух векторов иназываетсячисло равное произведению длин векторов на косинус угла между ними:

.

В последней формуле точка – знак скалярного умножения векторов.

,

таким образом, скалярное произведение равно произведению длины одного из векторов на проекцию второго вектора на первый.

Свойства скалярного произведения:

1. Скалярное произведение равно нулю тогда и только тогда, когда сомножители ортогональны: .

2. Скалярный квадрат вектора равен квадрату скаляра (квадрату длины вектора): .

3. Переместительное свойство: .

4. Распределительное свойство: .

5. Сочетательное свойство: .

Рассмотренные свойства дают возможность обращаться со скалярным произведением, как с произведением чисел:

.

6. Скалярное произведение разноименных ортов равно нулю:

.

Скалярное произведение одноименных ортов равно единице:

.

7. Если векторы заданы координатами , , то скалярное произведение равно сумме произведений одноименных координат: .

Простейшие задачи

1. Косинус угла между векторами определится по формуле:

.

2. Проекция вектора на вектор:

.

3. Условие ортогональности векторов:

.

Векторное произведение двух векторов

Правой связкой трех некомпланарных векторов ,,(взятых в таком порядке) с общим началом в точкеО (рис. 11) называется такое их расположение, когда кратчайший поворот первого вектора до совмещения со вторым смотрится с конца третьего вектора происходящим против хода часовой стрелки. В противном случае имеем левую связку векторов ,,(рис. 12).

Рис. 11 Рис. 12

Векторным произведением двух векторов иназывается новыйвектор , такой, что

1. ;

2. и ;

3. направлен так, что связка векторов ,,- правая.

Здесь знак умножения крестиком – знак векторного умножения векторов.

Свойства векторного произведения:

1. Векторное произведение равно нулю тогда и только тогда, когда вектора иколлинеарны: ||.

2. .

Таким образом, переместительный закон для векторного произведения не выполняется.

3. Распределительное свойство: .

4. Сочетательное свойство: .

5. Векторное произведение одноименных ортов равно нулю:

.

Векторное произведение разноименных ортов определяется следующей таблицей, из которой видно, что,,и т.д.

6. Векторное произведение в координатной форме есть определитель третьего прядка, у которого первая строка – координатные орты, вторая строка – координаты первого вектора-сомножителя, третья строка – координаты второго вектора-сомножителя: .

Простейшие задачи

1. Площадь параллелограмма, построенного на векторах и:

||= ||.

2. Площадь треугольника, построенного на векторах и:

.