13. Асимптоты функции

Различают вертикальные (параллельные оси ОY) и наклонные (не параллельные оси ОY) асимптоты графика функции.

Определение 13.1. Прямая называется вертикальной асимптотой графика функции, если хотя бы один из односторонних пределовилиравенили.

Например, график функции имеет вертикальную асимптоту, ибо,(см. рис. 13.1).

График функции может иметь бесконечное множество вертикальных асимптот, например график или.

Предположим, что функция определена для сколь угодно больших положительных значений аргумента.

Рис. 13.1

Определение 13.2. Прямая называется наклонной асимптотой графика функциипри, если функцияпредставима в виде

, (13.1)

где .

Теорема 13.1. Для того чтобы график функции имел принаклонную асимптоту, необходимо и достаточно, чтобы существовали два предельных значения

, . (13.2)

Доказательство. 1) Необходимость. Пусть график функции имеет принаклонную асимптоту, т.е. для функциисправедливо представление (13.1). Тогда

,

.

2) Достаточность. Пусть существуют предельные значения (13.2). По свойству предела функции второе из этих предельных значений равносильно равенству , где. Отсюда следует представление (13.1).

Заметим, что представление (13.1) эквивалентно равенству . Это означает, что приграфик функциинеограниченно приближается к прямой. Таким образом, наклонная асимптота характеризует поведение функции в бесконечности. При сколь угодно больших положительных значениях аргумента функцияприближенно может быть заменена линейной функцией.

Аналогично определяется наклонная асимптота и доказывается теорема 13.1 для случая . График функцииможет иметь самое большее две наклонные асимптоты (прии при).

Пример. Покажем, что в первом квадранте ветвь гиперболы приимеет наклонную асимптоту. Указанная ветвь является графиком функции. Используя необходимое и достаточное условия (13.2) существования наклонной асимптоты при, находим

,

.

Наряду с наклонной асимптотой рассматриваются также и асимптоты более сложного вида, например параболып – го порядка

.

14. Выпуклость и вогнутость функции. Точки перегиба графика функции

Отрезок, соединяющий две данные точки ив пространстве, есть множество точек. Значению параметрасоответствует точка, а значению параметра- точка.

Определение 14.1. Множество называется выпуклым, если вместе с любыми двумя точкамиэтому множеству принадлежит целиком и отрезок, соединяющий эти две точки.

Примерами выпуклых множеств являются отрезок, интервал, полуинтервал в пространстве Е, круг в пространстве , шар в пространстве.

Определение 14.2. Функция , заданная на выпуклом множестве, называется выпуклой (вогнутой) на этом множестве, если для любыхи любоговыполняется условие

, (14.1)

. (14.2)

В случае строгих неравенств говорят о строгой выпуклости и вогнутости. Заметим, что каждая вогнутая функция после умножения на минус единицу переходит в выпуклую функцию.

Геометрически условие выпуклости (вогнутости) функции одной переменной на интервалеозначает расположение графика этой функции на любом отрезкене выше (не ниже) хорды, соединяющей точкии(см. рис. 14.1).

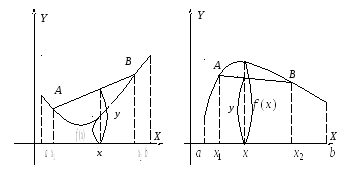
Рис. 14.1

Действительно, пусть функция выпукла на интервале, и пусть- любые две точки интервала, удовлетворяющие условию. Тогда в силу (14.1) для любоговыполняется неравенство

. (14.3)

Параметрические уравнения хорды АВ имеют вид

. (14.4)

В силу (14.4) условие выпуклости (14.3) запишется в виде

, (14.5)

что и требовалось доказать. В случае вогнутости функции рассуждения аналогичны.

Теорема 14.1. Если функция дважды дифференцируема на интервале, причем всюду на этом интервале, то функциявыпукла (вогнута) на интервале.

Доказательство. Пусть всюду на интервале. Исключая параметрt из уравнений (14.4), получим

. (14.6)

В силу (14.5) достаточно доказать, что для любых , удовлетворяющих условию, имеет место неравенство

. (14.7)

После простых алгебраических преобразований находим

. (14.8)

К квадратным скобкам в правой части (14.8) применим формулу Лагранжа. Получим

или

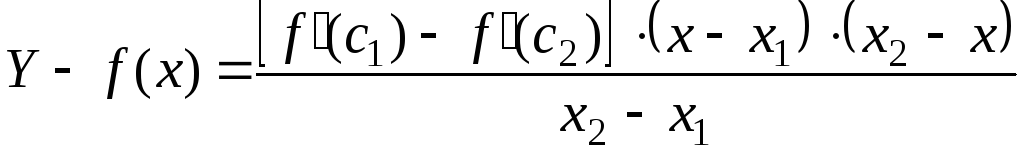, (14.9)

где ,. К квадратной скобке в правой части (14.9) снова применим формулу Лагранжа. Получим

, (14.10)

где . В силу дважды дифференцируемости функциина интерваледвукратное использование формулы Лагранжа правомерно. Так как по условию,,,, то из (14.10) следует неравенство (14.7).

Неравенство равносильно неравенству. Из последнего неравенства по доказанному выше следует, что функциявыпукла на интервале, а следовательно, функциявогнута на этом интервале. Теорема 14.1 доказана.

Поскольку , то в силу положительности и произвольностиусловиеравносильно условию

. (14.11)

Таким образом, согласно теореме 14.1 для выпуклости (вогнутости) функции на интерваледостаточно выполнение на этом интервале соответствующих условий (14.11). Последний результат следующим образом обобщается на случай функции нескольких переменных.

Теорема 14.2. Если функция задана в выпуклой области, дважды дифференцируема в этой области и во всех точках области справедливо неравенство

, (14.12)

то выпукла (вогнута) в указанной области.

Если же дифференциал второго порядка , то функциястрого выпукла (строго вогнута) в областиG.

Определение 14.3. Точка графика функцииназывается точкой перегиба этого графика, если существует такая окрестностьточки, в пределах которой по одну сторону точкифункциявыпукла, а по другую сторону вогнута.

Теорема 14.3. (Необходимое условие существования точки перегиба) Если есть точка перегиба графика функции, имеющей непрерывную производную второго порядка в точке, то.

Доказательство. Допустим противное, что . Тогда по свойству непрерывности функции найдется окрестностьточки, в пределах которой производная второго порядка имеет один и тот же знак. Отсюда по теореме 14.1 во всей этой окрестности функциялибо выпукла, любо вогнута, что противоречит наличию перегиба в точкеМ.

Теорема 14.4. (Достаточное условие существования точки перегиба). Если в окрестности точки , принадлежащей области определения функции, эта функция дважды дифференцируема, причем слева и справа от точкипроизводная второго порядкаимеет разные знаки, тоесть точка перегиба графика функции.

Утверждение теоремы непосредственно следует из определения 14.3 и теоремы 14.1.