9. Теорема Ферма

Теорема 9.1. Если функция определена в окрестноститочкис, дифференцируема в этой точке и в пределах значениеявляется наименьшим (наибольшим), то.

Доказательство. Ограничимся случаем наименьшего значения (для наибольшего значения рассуждения аналогичные). По определению наименьшего значения

.

Отсюда

, (9.1)

для всех , удовлетворяющих условию, и

, (9.2)

для всех , удовлетворяющих условию. В силу дифференцируемости функциив точкес существует предельное значение

. (9.3)

Если функция имеет производную в точкес, то в этой точке она имеет левую и правую производные, равные , т.е. существуют предельные значения

, .

Отсюда в силу (9.1) и (9.2) по свойству предела

, . (9.4)

Из (9.4) непосредственно следует, что .

10. Дифференциальные теоремы о среднем

Теорема Ролля. Если функция :

1. непрерывна на отрезке ;

2. дифференцируема на интервале ;

3. на концах отрезка имеет равные значения,

то на интервале найдется точкас такая, что .

Доказательство. Так как функция непрерывна на отрезке, то по свойству непрерывных функций на отрезке эта функция достигает на отрезкесвоего наименьшего значеният и своего наибольшего значения М. Возможны два случая:

1) ;

2) .

В первом случае в силу неравенств для всехимеем. Отсюда производнаяравна нулю в любой точке отрезка. Во втором случае, посколькуможно утверждать, что хотя бы одно из двух значенийт или М функция принимает в некоторой внутренней точкес отрезка . Так как функциядифференцируема в точкес и в окрестности этой точки достигает своего наименьшего или наибольшего значения, то по теореме Ферма. Теорема Ролля имеет простой геометрический смысл. Если функцияна отрезкеудовлетворяет всем трем условиям теоремы Ролля, то на графике этой функции найдется такая точка, в которой касательная параллельна осиОХ (см. рис. 10.1). В самом деле, значение равно угловому коэффициенту касательной к графику функциив точке.

Рис. 10.1

Теорема Коши. Если функции и:

1. непрерывны на отрезке ;

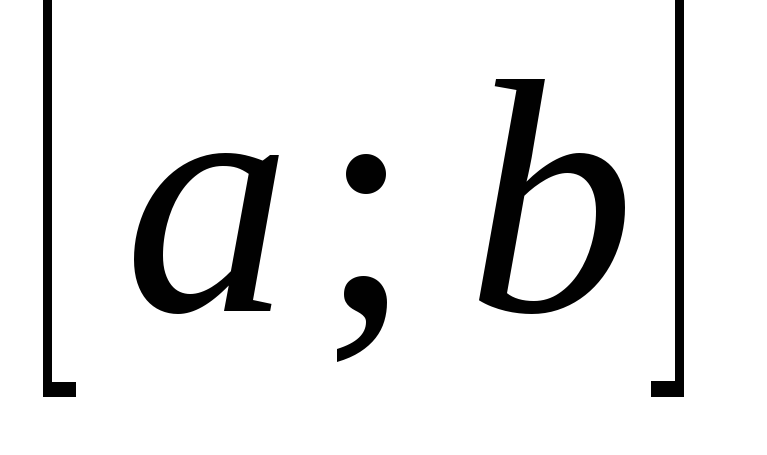2. дифференцируемы на интервале ;

3. производная отлична от нуля всюду на интервале,

то на интервале найдется точкас такая, что

. (10.1)

Доказательство. Прежде всего покажем, что . В противном случае функцияна отрезкеудовлетворяла бы всем трем условиям теоремы Ролля и по этой теореме на интерваленашлась бы точкатакая, что. Последнее противоречит третьему условию доказываемой теоремы. Далее, рассмотрим следующую вспомогательную функцию

, (10.2)

где - некоторое число. Функция (10.2) непрерывна на отрезкекак линейная комбинация непрерывных функций и дифференцируема на интервалекак линейная комбинация дифференцируемых функций, причем

. (10.3)

Выберем число так, чтобыили в силу (10.2)

.

Так как , то такой выборвозможен, причем

. (10.4)

При указанном выборе функциябудет удовлетворять всем трем условиям теоремы Ролля. По этой теореме на интерваленайдется точкас такая, что или в силу (10.3). Отсюда

. (10.5)

Из (10.4) и (10.5) следует утверждение теоремы (10.1).

Теорема Лагранжа. Если функция непрерывна на отрезкеи дифференцируема на интервале, то на интерваленайдется точкас такая, что

. (10.6)

Теорема Лагранжа является частным случаем теоремы Коши при . Действительно, функциянепрерывна и дифференцируема на всей числовой оси, причем. По теореме Коши на интерваленайдется точкас такая, что

.

Отсюда следует утверждение теоремы (10.6).

Рис. 10.2

Для выяснения геометрического смысла теоремы Лагранжа заметим, что величина есть угловой коэффициент секущей, проходящей через точкииграфика функции, аесть угловой коэффициент касательной к графику этой функции в точке. Формула Лагранжа (10.6) означает, что на графике функциимежду точкамиА и В найдется точка С, касательная в которой параллельна секущей АВ (см. рис. 10.2).

Во многих случаях удобнее записывать формулу Лагранжа в виде, несколько отличном от (10.6). Положим

, (10.7)

где . Очевидно,. Из (10.7) выводим

. (10.8)

Используя (10.8), формулу Лагранжа можно переписать в идее

, (10.9)

где . Если переобозначить,, то формула Лагранжа (10.9) примет вид

. (10.10)

Формула Лагранжа в форме (10.10) дает точное выражение для приращения функции в точкех, соответствующего приращению аргумента. По этой причине формула Лагранжа называется еще формулой конечных приращений.

Рассмотрим два следствия из формулы Лагранжа.

Теорема 10.1. Если функция дифференцируема на интервале

и всюду на этом интервале , то функцияпостоянна на этом интервале.

Доказательство. Пусть - некоторая фиксированная точка на интервале, ах – любая точка на этом интервале. Отрезок целиком принадлежит интервалу. Поэтому функциядифференцируема на отрезкеи, следовательно, непрерывна на этом отрезке. По теореме Лагранжа внутри отрезканайдется точкас такая, что

. (10.11)

Согласно условию производная функции всюду на интервалеравна нулю. Отсюдаи в силу (10.11), для любого.

Теорема 10.2. (Достаточное условие монотонности функции на интервале). Если функция дифференцируема на интервале, причем всюду на этом интервале, то функциявозрастает (убывает) на этом интервале.

Доказательство. Рассмотрим случай ( длярассуждения аналогичные). Пусть,- любые две точки интервала, удовлетворяющие условию. Так как отрезокцеликом принадлежит интервалу, то функциядифференцируема и, следовательно, непрерывна на этом отрезке. По теореме Лагранжа на интерваленайдется точкас такая, что

. (10.12)

Но производная всюду положительна на интервалеи, в частности, в точкес. Значит, в равенстве (10.12) , и кроме того,в силу выбора точеки. Следовательно, правая часть (10.12) положительна, отсюдаили. Что и требовалось доказать.

Заметим, что положительность (отрицательность) производной на интервалене является необходимым условием возрастания (убывания) функциина этом интервале. Например, функциявозрастает на всей числовой оси, но производнаяне всюду положительна, так как.

В теоремах Ролля, Коши и Лагранжа фигурирует некая «средняя» точка с, значение которой неизвестно. Однако, как будет видно далее, эти теоремы, носящие название дифференциальных теорем о среднем, лежат в основе многих формул и теорем математического анализа.